船舶运动自动控制可大体概括为以下5类情况[1]:1)大洋航行自动导航;2)港区航行及自动靠离泊;3)拥挤水道航行或大洋航行自动避碰;4)船舶减摇控制;5)无人航海载运工具控制。其中的第5类控制问题,恰好体现了船舶运动控制发展的新趋势[2]。自主式水下潜器(Autonomous Underwater Vehicle,AUV)的控制问题正属于其中的第5类控制情况。
人的潜水深度有限,而且水下环境也较为恶劣,自主式水下潜器因为具有智能化、安全、活动范围大、机动性好等方面的优点,目前已经发展成为了开发海洋与代替潜水员进行各种水下作业工作的重要工具。如在民用生产生活中,可用于深海石油勘测、航道排障、海底施工、港口作业、深海沉船考察、海上救助打捞及钻井平台水下结构检修等;在军事应用方面,可用于水下目标侦察、援潜、扫雷和救生等。在海洋开发工作中,自主式水下潜器起到的作用已经愈来愈重要,与此同时,对自主式水下潜器的性能要求也变得愈来愈高[3 -4]。
由于受燃料消耗、水压、速度变化等因素的影响,自主式水下潜器的数学模型参数具有较大的不确定性[5 -6],这给自主式水下潜器的控制系统设计带来了较大困难,因此适宜采用鲁棒控制方法来设计水下潜器的控制系统。近年来,许多不同的控制方法已经被应用到自主式水下潜器的各种运动控制研究中,如定量反馈控制、H∞鲁棒控制、模糊控制、滑模控制、线性二次型优化控制[5 -9]等方法。文献[5]为了解决水下潜器纵向姿态角控制问题,采用定量反馈理论设计了一种鲁棒控制器,但设计过程中需要根据经验预先设计出许多的性能指标并构造出适宜的频率响应模板,具有较大的盲目性。文献[6]利用定量反馈理论对H∞鲁棒控制器进行优化调整后,设计出了一种可用于水下潜器纵向姿态角控制的H∞鲁棒控制器,但控制器设计过程存在较大经验依赖性和盲目性。文献[7]将模糊控制与神经网络相结合,提出了一种基于模糊控制的水下潜器沉浮控制方法,但其精准的模糊规则难以获取,当规则过多,其计算负载将增加。文献[8]针对水下潜器的姿态和位置控制问题,设计出了一种基于高阶滑模算法的模型无关控制器,但是因为滑模控制方法自身的特性,使得系统仍然会出现一定的抖动现象。
PIλ Dμ 控制器的概念是由Podlubny在1997年时提出的[10]。PIλ Dμ 控制器除了兼具常规PID控制器的优点外,由于分数阶微积分自身的特性,分数阶控制器还具有许多整数阶控制器无法实现的优越性,其微分阶次μ和积分阶次λ可以进行实数范围内的任意设置,这使得PIλ Dμ 控制器具有比常规PID控制器更灵活的控制结构。近年来,一些研究者已经将PIλ Dμ 控制方法应用于航海领域,如船舶航向控制、船舶横摇控制和船舶电站柴油机调速系统控制[11 -13],并取得了较好的控制效果。
本文针对水下潜器纵向姿态角控制的稳定性问题,进行分数阶PID控制方法研究。在分数阶PID控制器的设计过程中,引入ITAE准则对分数阶PID控制器的参数进行优化,快速获得分数阶PID控制器的优化参数。同时本文对分数阶PID控制器和常规PID控制器的控制性能进行仿真实验对比,探讨2种控制器的稳态性能及鲁棒性。
1 分数阶微积分及分数阶PID控制器 1.1 分数阶微积分分数阶微积分是传统整数阶微积分的直接拓展,但它比整数阶微积分具有更广泛的适用性。所谓的分数阶微积分是指阶次为非整数的微积分,它可以实现任意阶次的微积分。分数阶微积分的算子可以由整数阶微积分的算子直接扩展得到,其定义如下[14 -15] :
| $ {}_aD_t^\alpha = \left\{ {\begin{array}{*{20}{c}}\!\!\!\!\!\!\! \!\!\!\!\!\!{\displaystyle\frac{{{{\rm{d}}^\alpha }}}{{{\rm{d}}{t^\alpha }}},{\mathop{ Re}\nolimits} \left( \alpha \right) > 0}\text{,}\\[7pt] \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{1,{\mathop{ Re}\nolimits} \left( \alpha \right) = 0}\text{,}\\[5pt] {\int_a^t {{{\left( {{\rm{d}}\tau } \right)}^{ - \alpha }},{\mathop{ Re}\nolimits} \left( \alpha \right) < 0} }\text{。} \end{array}} \right. $ | (1) |
式中:a为算子的下限;t为算子的上限;α为分数阶微积分的阶次,可以是任意复数,本文假定α为实数。
目前,在分数阶微积分理论中较为常用的定义有以下4种[14, 15] :
1)Cauchy的表达式为:
| $ {}_aD_t^\alpha f\left( t \right) = \frac{{\Gamma \left( {\alpha + 1} \right)}}{{2{{\pi j}}}}\int_C {\frac{{f\left( \tau \right)}}{{{{\left( {\tau - t} \right)}^{\alpha + 1}}}}{\rm{d}}\tau } \text{,} $ | (2) |
式中C为包围f(t)单值与解析开区域的光滑曲线。
2)Grunwald-Letnikov的表达式为:
| $ _a^{GL}D_t^\alpha f\left( t \right) = \mathop {\lim }\limits_{h \to 0} \frac{1}{{{h^\alpha }}}\sum\limits_{j = 0}^{\left[ {\left( {t - a} \right)/h} \right]} {\left( { - 1} \right)^j}\left( {\begin{array}{*{20}{c}} \alpha \\ j \end{array}} \right)f\left( {t - jh} \right), $ | (3) |
式中:
3)Riemann-Liouville的表达式为:
| $ {}_a^{RL}D_t^\alpha f\left( t \right) = \frac{1}{{\Gamma \left( {n - \alpha } \right)}}\frac{{{{\rm{d}}^n}}}{{{\rm{d}}{t^n}}}\left[ {\int_a^t {\frac{{f\left( \tau \right)}}{{{{\left( {t - \tau } \right)}^{\alpha - n + 1}}}}} {\rm{d}}\tau } \right]\text{,} $ | (4) |
式中:
4)Caputo的表达式为:
| $ {}_0D_t^\alpha f\left( t \right) = \frac{1}{{\Gamma \left( { - \alpha } \right)}}\int_0^t {\frac{{f\left( \tau \right)}}{{{{\left( {t - \tau } \right)}^{1 + \alpha }}}}} {\rm{d}}\tau \text{,} $ | (5) |
式中α < 0。
1.2 分数阶PID控制器PIλ Dμ 控制器的传递函数模型为:
| $ {G_c}\left( s \right) = {k_p} + \frac{{{k_i}}}{{{s^\lambda }}} + {k_d}{s^\mu }\text{。} $ | (6) |
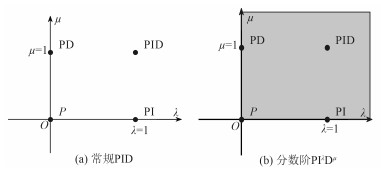
PIλ Dμ 控制器的示意图如图 1所示。其中,横轴为PIλ Dμ 控制器的积分阶次λ,纵轴为PIλ Dμ 控制器的积分阶次μ。常规的PI控制器、PD控制器和PID控制器均为PIλ Dμ 控制器平面内的一个点。
|
图 1 分数阶PIλ Dμ 控制器示意图 Fig. 1 Diagram of fractional-order PIλ Dμ controller |
通过比对可知,常规PID的λ与μ的值均为1,是一种特例分数阶PID;与此类似,当λ=1,μ=0对应常规PI控制器;当λ=0,μ=1对应常规PD控制器。此外,由于分数阶PID的积分阶次λ与微分阶次μ可以是任意实数,这使得分数阶PID控制器与整数阶PID控制器相比,具有更灵活的控制结构与优越的性能。
2 水下潜器的分数阶PID控制器设计 2.1 水下潜器的传递函数模型水下潜器的纵向姿态角控制通常选取弹道中极具代表性的3个典型工作点作为研究对象[16] ,这3个典型工作点分别位于初始发射阶段、中间阶段与目标接近阶段。假设舵角δ作为输入信号,水下潜器的俯仰角ψ作为输出信号,可以获得不同阶段水下潜器的传递函数模型P1,P2和P3。
| $ \begin{array}{l} {P_1} =\displaystyle \frac{{{{13}}{{.2 s + 73}}{{.5}}}}{{{\rm{0}}{{.015 }}{{{s}}^{\rm{4}}}{\rm{ + 1}}{\rm{.1879 }}{{{s}}^{\rm{3}}}{\rm{ + 13}}{\rm{.0786 }}{{{s}}^{\rm{2}}}{\rm{ + 36}}{{.9526 s}}}}\text{,}\\[10pt] {P_2} =\displaystyle \frac{{{{ 80}}{{.4 s + 687}}{\rm{.6}}}}{{{\rm{0}}{\rm{.015 }}{{{s}}^{\rm{4}}}{\rm{ + 1}}{\rm{.3809}}{{{s}}^{\rm{3}}}{\rm{ + 27}}{\rm{.2566 }}{{{s}}^{\rm{2}}}{\rm{ + 124}}{{.1385 s}}}}\text{,}\\[10pt] {P_3} =\displaystyle \frac{{{\rm{152}}{{.7 s + 1692}}{\rm{.8}}}}{{{\rm{0}}{\rm{.015 }}{{{s}}^{\rm{4}}}{\rm{ + 1}}{\rm{.5145}}{{{s}}^{\rm{3}}}{\rm{ + 37}}{\rm{.5676 }}{{{s}}^{\rm{2}}}{\rm{ + 218}}{{.031 s}}}}\text{。} \end{array} $ | (7) |
在设计水下潜器纵向姿态角控制的PIλ Dμ 控制器时,选取P2为基准模型,其他2个模型用于验证所设计控制器的鲁棒性能[16] 。在控制器设计过程中,为了能快速获得PIλ Dμ 控制器的优化参数,提高控制器的控制性能,引入如下ITAE准则:
| $ {J_{\rm{ITAE}}} = \int_0^\infty {t\left| {e\left( t \right)} \right|} {\rm{d}}t \text{,} $ | (8) |
通过数值方法对ITAE准则指标进行优化,则可以得到优化后的PIλ Dμ 控制器参数,kp =0.6,ki =1.6,kd =0.52,λ=0.1,μ=0.64。即优化PIλ Dμ 控制器为:
| $ {G_1} = 0.6 + \frac{{1.6}}{{{s^{0.1}}}} + 0.52{s^{0.64}} \text{,} $ | (9) |
此外,采用常规PID控制器的设计方法[14] ,可获得常规PID控制器如下。
| $ {G_2} = \frac{{{\rm{39}}{{.23(s + 16}}{{.13)(s + 0}}{\rm{.2)}}}}{{{{s(s + 125)}}}} \text{。} $ | (10) |
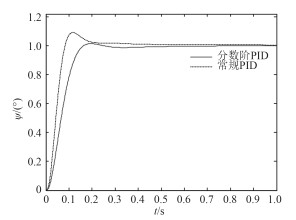
针对基准模型P2,进行水下潜器俯仰角闭环控制单位阶跃变化时的瞬态响应仿真实验,得到分数阶PID控制器和常规PID控制器的控制性能结果曲线,如图 2所示。
|
图 2 P2模型的仿真结果曲线 Fig. 2 Simulation result curve of modelP2 |
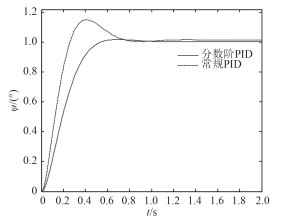
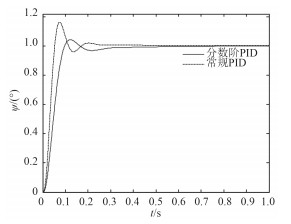
其中,常规PID控制器的调节时间为ts =0.225 s,上升时间为tr =0.052 s,超调量σ%=9.2%。PIλ Dμ 控制器的调节时间为ts =0.30 s,上升时间为tr =0.17 s,超调量σ%=1.5%。2种控制器对模型P1和模型P3的控制仿真结果曲线分别如图 3和图 4所示。
|
图 3 P1模型的仿真结果曲线 Fig. 3 Simulation result curve of modelP1 |
|
图 4 P3模型的仿真结果曲线 Fig. 4 Simulation result curve of modelP3 |
对比以上的仿真结果可知,本文所设计的PIλ Dμ 控制器的控制效果明显优于常规PID控制器,具有更好的稳态性能,且PIλ Dμ 控制器对3种模型均表现出了更为优越的鲁棒性能,能很好地克服水下潜器由于外界因素干扰而导致的模型不确定性的影响。本文所设计的PIλ Dμ 控制器具有鲁棒性强、稳定性好等优点。
4 结语针对水下潜器纵向姿态角控制存在的模型不确定性且系统对控制器鲁棒性能要求较高的特点,引入ITAE准则后对控制器参数进行优化,设计出了一种分数阶PID控制器。仿真结果表明,本文中设计出的分数阶PID控制器可用于水下潜器的纵向姿态角控制,控制器的性能优于常规PID控制器,且控制器具有更为良好的鲁棒性能。
| [1] | 张显库. 船舶运动简捷鲁棒控制[M]. 北京: 科学出版社, 2012 . |
| [2] | ROBERTS G N. Trends in marine control systems[J]. Annual Reviews in Control , 2008, 32 (2) :263–269. DOI:10.1016/j.arcontrol.2008.08.002 |
| [3] | SHEN Y X, SHAO K Y, REN W J, et al. Diving control of autonomous underwater vehicle based on improved active disturbance rejection control approach[J]. Neurocomputing , 2016, 173 :1377–1385. DOI:10.1016/j.neucom.2015.09.010 |
| [4] | KIM J, JOE H, YU S C, et al. Time-delay controller design for position control of autonomous underwater vehicle under disturbances[J]. IEEE Transactions on Industrial Electronics , 2016, 63 (2) :1052–1061. DOI:10.1109/TIE.2015.2477270 |
| [5] |
肖永利, 张琛, 吴庆宪. QFT在水下潜器控制系统设计中的应用[J]. 上海交通大学学报 , 1999, 33 (4) :446–449.
XIAO Yong-li, ZHANG Chen, WU Qing-xian. Application of QFT in Design of Underwater Vehicle Control System[J]. Journal of Shanghai Jiaotong University , 1999, 33 (4) :446–449. |
| [6] |
肖永利, 张琛, 李振波, 等. 水下潜器的鲁棒控制系统设计[J]. 上海交通大学学报 , 1999, 33 (11) :1348–1351.
XIAO Yong-li, ZHANG Chen, LI Zhen-bo, et al. Design of robust control system for underwater vehicle[J]. Journal of Shanghai Jiaotong University , 1999, 33 (11) :1348–1351. |
| [7] | FOSSEN T I. Guidance and control of ocean vehicles[M]. New York: Wiley, 1994 . |
| [8] |
丰少伟, 彭鹏菲, 姜俊. 基于模糊控制的水下潜器沉浮控制方法[J]. 电子设计工程 , 2011, 19 (5) :19–21, 25.
FENG Shao-wei, PENG Peng-fei, JIANG Jun. Ups and downs control method of underwater submersible vehicle based on fuzzy control[J]. Electronic Design Engineering , 2011, 19 (5) :19–21, 25. |
| [9] |
邓春楠, 葛彤, 吴超. 基于高阶滑模控制器的水下潜器运动控制[J]. 海洋工程 , 2013, 31 (6) :53–58, 96.
DENG Chun-nan, GE Tong, WU Chao. Underwater vehicle motion control based on high order sliding controller[J]. The Ocean Engineering , 2013, 31 (6) :53–58, 96. |
| [10] | PODLUBNY I, DORCAK L, KOSTIAL I. On fractional derivatives, fractional-order dynamic systems and PIλDμ controllers[C]//Proceedings of the 36th IEEE Conference on Decision and Control. San Diego, USA: IEEE, 1997. |
| [11] |
李光宇, 郭晨, 李延新. 基于改进粒子群算法的USV航向分数阶控制[J]. 系统工程与电子技术 , 2014, 36 (6) :1146–1151.
LI Guang-yu, GUO Chen, LI Yan-xin. Fractional-order control of USV course based on improved PSO algorithm[J]. Systems Engineering and Electronic , 2014, 36 (6) :1146–1151. |
| [12] | FAIEGHI M R, NADERI M, JALALI A A. Design of Fractional-Order PID for ship roll motion control using chaos embedded PSO algorithm[C]//Proceedings of the 2nd International Conference on Control, Instrumentation and Automation (ICCIA). Shiraz, Iran: IEEE, 2011: 606-610. |
| [13] |
李志民, 孙其振, 孙勇, 等. 基于BF-PSO的船舶电站柴油机分数阶控制器[J]. 控制工程 , 2012, 19 (3) :515–518.
LI Zhi-min, SUN Qi-zhen, SUN Yong, et al. Design of fractional-order controller for diesel engine system based on BF-PSO[J]. Control Engineering of China , 2012, 19 (3) :515–518. |
| [14] | 薛定宇, 陈阳泉. 高等应用数学问题的MATLAB求解[M].3版. 北京: 清华大学出版社, 2013 . |
| [15] | 薛定宇. 控制系统计算机辅助设计-MATLAB语言与应用[M].3版. 北京: 清华大学出版社, 2012 . |
| [16] | ZHANG X K, JIN Y C. Transfigured loop shaping controller and its application to underwater vehicle[J]. International Journal of Automation and Computing , 2005, 2 (1) :48–51. DOI:10.1007/s11633-005-0048-7 |
 2016, Vol. 38
2016, Vol. 38
