2. 中国舰船研究设计中心, 湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
电磁环境的计算,尤其是大规模阵列天线在复杂结构下的电磁参数的计算,对于国防建设有着十分重要的意义,这也是计算电磁学的研究热点之一。但在解决飞机、舰船等实际目标的高频电磁特性时,往往会遇到计算量巨大和计算机硬件计算能力不足的矛盾。船用设备高速发展的需求是船舶电磁兼容技术主要背景[1]。而舰载天线的电磁辐射是船舶电磁环境的主要来源,其中相控阵天线有电扫描和快速变换方向的优势, 使雷达性能得到很大提升。由于电子技术的进步和电子器件费用的急剧下降,相控阵天线使用场合越来越多,越来越多的民用平台装备了相控阵雷达,用于天气预报、导航、探测等。相控阵雷达天线一般包括几千个小阵元天线,总功率较大。为进行电磁干扰和电磁安全性分析,需对这些区域进行电磁场强预测。但现有技术难以准确、迅速地求解相控阵天线的近场电磁环境。本文针对复杂结构平台下的相控阵天线的电磁环境的求解给出一种快速求解方案。
1 阵列天线电磁环境计算建模相控阵天线的近场区域相对于阵中的阵元而言常常是远场区[2 -4]。本文快速求解方案主要包括以下3个方面的内容:
1)船用相控阵天线在自由空间的辐射建模。在天线阵元数量超过1 000以上的相控阵天线中,可以近似认为各个天线具有相似的辐射特性,在该建模过程中建立适当大小的子阵列,并使用商业工具计算获取阵元在考虑耦合效应时的远场辐射特性数据。
2)船用相控阵天线的辐射场在复杂结构船体上的传播建模。本文采用高频近似算法,该建模过程旨在通过镜像源法及相关加速手段快速获取射线传播路径。
3)船用相控阵天线在复杂平台下的近场求解。利用阵列天线的近场为阵元远场的特点,首先用GO[5 -7]算法计算得到每个阵元在有复杂结构对象影响下的电磁场,然后使用叠加原理对各个阵元在复杂结构船体影响下的场进行矢量叠加并进行功率校正得到阵列天线的场。本文使用MPI[8 -9]并行计算技术,以实现快速的射线路径搜索。
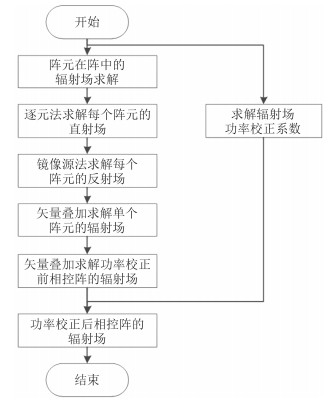
图 1给出了本文提出的方案的系统流程图。文中方案首先借鉴有源方向图法处理得到单个阵元在阵中的远场辐射特性数据。然后求解每个阵元的直射场,并使用镜像源方法求解单个阵元的反射路径,按照GO算法计算得到单个阵元的反射场,然后矢量叠加得到单个阵元在复杂结构平台下的场。对每一个阵元实施上述计算过程,并对每个阵元的场进行矢量叠加即可得到功率校正前相控阵天线在复杂结构平台下的辐射场。完成上述过程后即可得到相控阵天线在复杂结构下单个场点的电磁场,不同的场点进行遍历计算即完成近场计算工作。最后考虑到实际天线可能并不是辐射出单位功率,需要根据辐射场功率校正公式对其校正即得到最终结果。
|
图 1 复杂结构平台下的相控阵天线电磁环境求解方案系统流程图 Fig. 1 System flowchart of phased array antenna electromagnetic environment resolution |
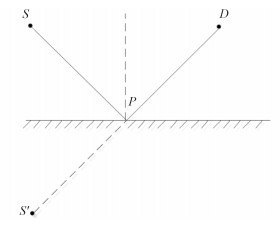
光线传播过程中满足费马定理,其内涵主要包括:入射角等于反射角与光程最短。可以利用镜像原理,首先求出源点S(或上一个反射点)关于三角面片的对称点(即虚拟源)S′,计算虚拟源和场点D所成直线与三角面片所在平面的交点P,如图 2所示。
|
图 2 镜像源法示意图 Fig. 2 Schematic diagram of image source method |
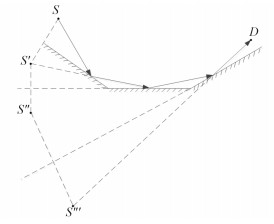
在实现过程中,需要处理所有面片。依次找出源点S相对于第一个三角面片的镜像源S′,然后找出镜像源S′相对于下一个三角面片的镜像源S″,以此类推知道所有的镜像源全部找到为止。然后连接场点与最后一个镜像源,如此递推直到源点S。上述的实现方法也可以逆向实现,即从场点开始依次求出场点的各个镜像场点,本文中采用的是上面介绍的方法。镜像源法对多三角面片的射线寻径示意图如图 3所示。
|
图 3 多三角面片寻径示意图 Fig. 3 Schematic diagram of routing on muti-facets |
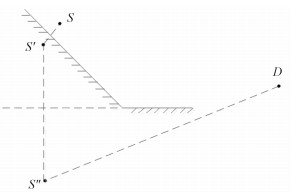
在寻径过程中,需要以下2种不符合射线传播原理的情况:一是镜像源在下一个寻径的三角面片的背面,如图 4所示;二是镜像源(或源点)与邻近的镜像源(或者场点)连线的交点不在三角面片上,如图 5所示。

|
图 4 第1种情况 Fig. 4 The first illegal condition |
|
图 5 第2种情况 Fig. 5 The second illegal condition |
对于船体对象,在剖分网格形成三角面片后需要进行树形结构的组织,具体实现方法可以根据上面的镜像源法推导得出。设若共有n个三角面片,在每个三角面片寻找镜像源之后,下一个三角面片的选取共有n -1个选择,而在第2个三角面片选择确定后,第3次选取三角面片时依旧有n -1个选择,以此类推。在反射一定次数Tmax之后,场已经衰减到足够小,此时认为该路径不合法。
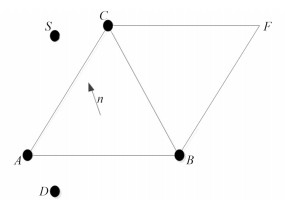
3 基于面片的实时空间区域二分算法源点(或某个镜像源)S和某个三角面片选定以后,虽然不确定射线的方向和反射点,但是可以预测的是反射线与下一个三角面片有交点的情况只在一种情况下成立,即源点与下一个三角面片在该选定三角面片的同侧。
对于三角面片△ABC,首先求解出法向量:
| $ \overrightarrow n = \overrightarrow {AB} \times \overrightarrow {AC}\text{。} $ | (1) |
如果源点S在法向量
| $ \overrightarrow n \overrightarrow { \cdot AS} > 0\text{。} $ | (2) |
此时若下一个三角面片满足下一次反射的条件,则三角面片上的3个顶点不可能全在法向量所指的背侧,若任取三角面片的其中一个点D,其都满足
| $ \overrightarrow n \overrightarrow { \cdot AD} < 0 \text{,} $ | (3) |
则此三角面片不满足下一次反射的条件。
若源点在法向量所指的背侧,即
| $ \overrightarrow n \overrightarrow { \cdot AS} < 0\text{,} $ | (4) |
此时判断准则为
| $ \overrightarrow n \overrightarrow { \cdot AD} > 0\text{。} $ | (5) |
|
图 6 空间区域划分示意图 Fig. 6 Schematic diagram of real-time spatial region bipartite accelerated method |
采用空间区域划分的方式,计算量约为:
| $ O = M \times N \times (1 + \frac{{n \times {{(n - 1)}^{{T_{\rm max}} - 1}}}}{{{2^{{T_{\rm max}}}}}}) $ | (6) |
其中Tmax为最大路径深度。对反射场的路径搜索效率提升大约为:
| $ \eta \approx (1 - \frac{1}{{{2^{{{{T}}_{\rm max}}}}}}) \times 100\% \text{。} $ | (7) |
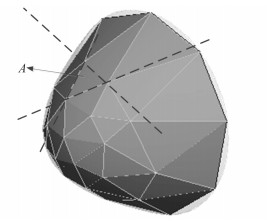
然而,使用上式并能足够精确地估计算法的效率。当处理的对象是一个任意的凸面体时,其上的每一个三角面片的背面均包含有该凸面体的所有面片,如图 7所示,即下一次反射时,不需要考虑其他面片。图中所示为粗网格剖分(为了使结果清晰可见)的一个抛物面,如果点源在抛物面的外侧,则对任意选取的一个面片A,所有的其他面片均在其背侧,即不符合下次反射的条件。此时的计算量为:
|
图 7 典型凸多面体结构的快速寻径示意图 Fig. 7 Schematic diagram of fast routing on convex polyhedron structure |
| $ O = M \times N \times (1 + n)\text{。} $ | (8) |
计算量减少约
对于给定的简化飞机模型,源点(0,0,0),场点(3,-6,0.5)时,通过本文中使用的程序计算得到的射线如图 8所示,其中反射点坐标为(0.724 138 02,2.800 000 2,0.120 689 66)

|
图 8 简化飞机模型下的路径搜索计算实例 Fig. 8 Calculation instance of routing under simplified plane model calculated by program in the paper |
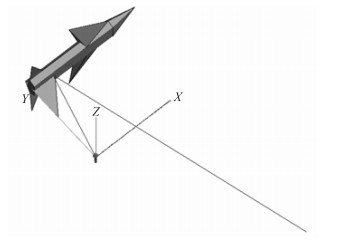
为了进行对比,对同一模型使用FEKO进行射线计算,图 9给出了FEKO在计算同一模型时的计算结果,表 1给出了源点Q,场点S和中间1次反射点R的数据。
|
图 9 简化飞机模型下的路径搜索FEKO计算实例 Fig. 9 Instance of reflect ray under simplified plane model calculated by FEKO |
|
|
表 1 FEKO计算的射线数据 Tab.1 Data of ray calculated by FEKO |
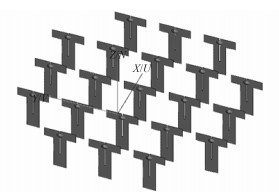
对于上面建立的简化飞机模型,考虑到商业软件(本文主要与FEKO的计算结果进行对比)的计算能力,建立了21元小阵列,如图 10所示,表 2给出了阵元坐标。
|
图 10 FEKO建立的21元阵列天线模型 Fig. 10 21 elements subset model of phased array antenna setup by FEKO |
|
|
表 2 21元阵列阵元分布数据 Tab.2 Parameters of 21 elements subsets |
图 11和图 12给出了分别使用本文的程序和FEKO计算得到的场,表 3和表 4分别表示本文和FEKO计算简化飞机模型对象时的场点值,经过简单计算可以知二者相差3 dB左右。

|
图 11 简化飞机模型结构下的阵列天线的电磁环境计算实例 Fig. 11 Calculation instance of phased array antenna electromagnetic environment under simplified plane model |

|
图 12 简化飞机模型结构下的阵列天线的电磁环境FEKO计算实例 Fig. 12 Instance of phased array antenna electromagnetic environment under simplified plane model calculated by FEKO |
|
|
表 3 本文程序计算简化飞机模型场点结果 Tab.3 Field result of simplified plane model calculated by program used in the paper |
|
|
表 4 FEKO计算简化飞机模型场点结果 Tab.4 Field result of phased array antenna electromagnetic environment under simplified plane model calculated by FEKO |
本文给出的方案能够极大简化射线寻径过程,并且使用程序优化技术能够快速获取相控阵天线的近场数据。文中建立了21元天线阵列,对该阵列在组合结构(简化飞机模型)平台影响下的电磁场进行了计算,同时在FEKO中使用UTD算法计算得到了该阵列在相同组合结构下的电磁场,结果表明二者具有比较接近的计算精度(基本不超过3 dB),即用本文的计算方法计算得到的结果具有足够的实用价值。
| [1] | 邵开文, 马运义. 舰船技术与设计概论[M]. 北京: 国防工业出版社, 2005 . |
| [2] |
历园园, 翟助群, 李思, 等. 基于高频算法的舰船电磁环境研究[J]. 中国舰船研究 , 2015, 10 (2) :15–21, 34.
LI Yuan-yuan, ZHAI Zhu-qun, LI Si, et al. Research on the electromagnetic environment of ships based on the high frequency algorithm[J]. Chinese Journal of Ship Research , 2015, 10 (2) :15–21, 34. |
| [3] |
潘龙, 朱志宇. 应用于舰载天线电磁兼容性分析的改进多层快速多极子算法[J]. 中国舰船研究 , 2015, 10 (2) :47–54.
PAN Long, ZHU Zhi-yu. An improved MLFMA algorithm for the electromagnetic compatibility analysis of shipboard antennas[J]. Chinese Journal of Ship Research , 2015, 10 (2) :47–54. |
| [4] |
郭旸, 王向华, 胡骏. 基于函数语言的并行FDTD算法新实现及其在航空母舰甲板表面电磁场分布问题仿真中的应用[J]. 中国舰船研究 , 2015, 10 (2) :35–39, 54.
GUO Yang, WANG Xiang-hua, HU Jun. A new parallel implementation for FDTD algorithm using function languages and its application for simulating field distribution on a ship platform[J]. Chinese Journal of Ship Research , 2015, 10 (2) :35–39, 54. |
| [5] |
周文明, 宋建社, 郑永安, 等. 复杂目标电磁散射混合算法[J]. 电波科学学报 , 2007, 22 (5) :884–890.
ZHOU Wen-ming, SONG Jian-she, ZHENG Yong-an, et al. A hybrid method for computing high-frequency RCS of complex radar targets[J]. Chinese Journal of Radio Science , 2007, 22 (5) :884–890. |
| [6] | 李冬虎.基于KD-Tree的电磁散射高频分析[D].南京:南京理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10288-1014175472.htm |
| [7] | 李金星, 江旺强, 张民.基于图形遮挡技术与GO-PO方法的电大复杂目标散射特性分析[C]//中国电子学会微波分会. 2015年全国微波毫米波会议论文集.合肥:中国电子学会, 2015: 4. |
| [8] |
刘战合, 何政道, 李莹, 等. 雷达散射截面并行计算中的MPI实现技术研究[J]. 航空计算技术 , 2009, 39 (4) :109–112.
LIU Zhan-he, HE Zheng-dao, LI Ying, et al. On MPI implementation of radar cross section parallel computation[J]. Aeronautical Computing Technique , 2009, 39 (4) :109–112. |
| [9] | 邹光先.集群环境下基于MPI的并行多层快速多极子方法研究[D].成都:电子科技大学, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10614-2004128330.htm |
 2016, Vol. 38
2016, Vol. 38
