进入21世纪后,人类对海洋的开发利用更加深入,同时国防建设及海上运输也对船舶的运动控制提出了越来越高的要求。20世纪50年代采用PID控制的第一代船舶动力定位系统问世,随着计算机技术和现代控制理论的不断发展,各种新的控制方法,如变结构控制、神经网络控制、模糊控制、滑模控制、H∞控制、反步控制等控制方法,都先后应用于船舶航向控制。20世纪80年代初由Garcia和Morari提出了内模控制(IMC)方法,经过几十年的发展,内模控制方法己在一般形式的非线性系统上建立起比较完整的设计理论,同时其较好的鲁棒性、抗扰动性和对大时滞系统的控制使其得到了广泛应用[1]。
最近几十年来,逆系统方法在非线性解耦上有了飞速的发展,逆系统方法结构简单,概念清晰。通过构造α阶逆系统,将α阶逆系统与系统复合成伪线性系统。对伪线性系统进行内模控制,从而实现对原非线性系统的有效控制,此方法不但结构简单,而且易于实现。此外将内模控制与PID控制策略结合使用,仿真结果表明在有控制限幅的情况下仍能有满意的控制效果。
1 船舶运动的非线性模型在有风、浪、流共同作用的复杂海况下,无约束的船舶具有6个自由度的运动特征。这些运动均含有低频分量和高频分量。低频运动分量可以认为是由螺旋桨的推力、舵力、流力、风力和缓变的波浪漂移力等产生的;而高频运动分量主要是由波浪引起的一阶波频运动响应,而随波浪的起伏而往复,呈现出自动恢复原位的特性。动力定位控制的主要是水平面运动的位置和首向,即纵荡、横荡和首摇3个维度的控制[2-3]。
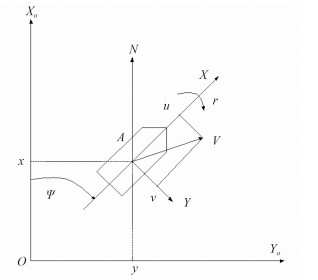
图 1所示为水面船舶运动参考坐标系,OX0Y0为大地坐标系,AXY为随船坐标系,随船坐标系的原点在船舶重心处。定义大地坐标系下的船舶位置和首摇角η=[x,y,ψ]T,随船坐标系AXY下的速度向量ν=[u,v,r]T。x,y,ψ分别为船舶在地理坐标系中的纵向位移、横向位移和首向角;u,v,r分别为船舶的纵荡、横荡和首摇速度。
|
图 1 船舶运动坐标系 Fig. 1 Vessels moving coordinate system |
船舶位移和速度的关系式:
| $ \dot \eta = \boldsymbol{R}(\psi )\nu {\rm{, }} $ | (1) |
即
| $ \left\{ {\begin{array}{*{20}{l}} {u = \dot y\sin \phi + \dot x\cos \phi }\text{,}\\ {v = \dot y\cos \phi - \dot x\sin \phi }\text{,}\\ {r = \dot \phi }\text{,} \end{array}} \right. $ |
大地坐标系与随船坐标系间的坐标转换矩阵:
| $ \boldsymbol{R}(\psi ) = \left[{\begin{array}{*{20}{c}} {\cos \psi }&{-\sin \psi }&0\\ {\sin \psi }&{\cos \psi }&0\\ 0&0&1 \end{array}} \right]{\rm{.}} $ | (3) |
船舶的低频运动由风、海流、二阶海浪和船舶推进器引起。T. I. Fossen在20世纪90年代提出了船舶在横荡、纵荡、首摇3个自由度的低频运动数学模型如下:
| $ \boldsymbol{M}\dot v + \boldsymbol{D}v = \tau + {R^{\rm{T}}}\left( \psi \right)b. $ | (4) |
式中:ν=[u,v,r]T,为船舶在低频运动下的速度向量;M为惯性矩阵,包括水动力附加质量矩阵,满足正定要求M=MT > 0;D为线性水动力阻尼系数矩阵。
| $ \begin{array}{l} \boldsymbol{M} = \left[{\begin{array}{*{20}{c}} {m-{X_{\dot u}}}&0&0\\ 0&{m-{Y_{\dot \nu }}}&{m{x_g}-{Y_{\dot r}}}\\ 0&{m{x_g} - {N_{\dot \nu }}}&{{I_z} - {N_{\dot r}}} \end{array}} \right], \\ \boldsymbol{D} = \left[{\begin{array}{*{20}{c}} {-{X_u}}&0&0\\ 0&{-{Y_\nu }}&{-{Y_r}}\\ 0&{ - {N_\nu }}&{ - {N_r}} \end{array}} \right]{\rm{, }} \end{array} $ | (5) |
| $ \tau = {\tau _e} + {\tau _c}{\rm{, }} $ | (6) |
| $ {\boldsymbol{\tau _e}} = \left[{\begin{array}{*{20}{c}} {{X_e}}\\ {{Y_e}}\\ {{N_e}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{X_{wind}} + {X_{wave}} + {X_{current}}}\\ {{Y_{wind}} + {Y_{wave}} + {Y_{current}}}\\ {{N_{wind}} + {N_{wave}} + {N_{current}}} \end{array}} \right]. $ | (7) |
式中:m为船舶质量;IZ为转动惯量;xg为船舶重心在随船坐标系中的x轴坐标值;
内模控制(Internal Model Control,IMC)是由20世纪50年代Smith提出的时滞补偿器发展演变而来,由于其良好的鲁棒性和抗扰动性等性能,自其产生以来,便得到了广泛应用。
内模控制主要的设计原理是采用相消法,将实际对象与对象模型相并联,对象模型逼近实际模型,同时控制器设计策略是使之逼近模型的动态逆,例外增加滤波环节以增强系统的鲁棒性。内模控制器结构简单,控制策略简单明了,参数调整方便容易。由于能清楚地表现出参数调节和闭环响应及鲁棒性之间的关系,因此能兼顾控制系统性能和鲁棒性[4-5]。
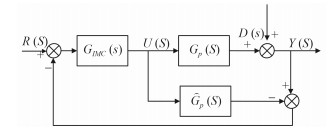
内模控制结构图如图 2所示。其中,Gp(S)为实际控制对象;
| $ \frac{{Y(s)}}{{R(s)}} = \frac{{{G_{IMC}}(s) \cdot {G_p}(s)}}{{1 + {G_{IMC}}(s) \cdot [{G_P}(s)-{{\hat G}_p}(s)]}}{\rm{, }} $ | (8) |
| $ {G_{IMC}}(s) = \frac{1}{{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over G} }_P}(s)}}f\left( s \right). $ | (12) |
|
图 2 IMC结构框图 Fig. 2 IMC structure diagram |
这样整个闭环系统响应为:
| $ \begin{array}{l} Y(s) = \frac{{{G_{IMC}}(s) \cdot {G_p}(s)}}{{1 + {G_{IMC}}(s) \cdot [{G_P}(s)-{{\hat G}_p}(s)]}} \cdot R(s) + \\ \;\;\;\;\;\;\;\;\;\;\frac{{1 - {G_{IMC}}(s) \cdot {{\hat G}_p}(s)}}{{1 + {G_{IMC}}(s) \cdot [{G_P}(s)-{{\hat G}_p}(s)]}} \cdot D(s){\rm{;}} \end{array} $ | (10) |
反馈信号为公式:
| $ \hat D(s) = [{G_P}(s)-{{\hat G}_p}(s)] \cdot U(s) + D(s){\rm{.}} $ | (11) |
可见,若系统控制对象模型准确,即
内模控制系统的设计主要是内模控制器的设计。其控制设计思想是:首先设计一个稳定的控制器,不考虑鲁棒性、扰动及约束等条件;然后引入低通滤波器,提高系统的运动控制性能和鲁棒性。内模控制器主要由:模型的逆和滤波器2部分组成。两者分别影响系统的响应性能和鲁棒性能。
| $ {G_{IMC}}(s) = \frac{1}{{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over G} }_p} - (s)}}f(s). $ | (12) |
式中:f(s)为IMC滤波器。
设计步骤如下:
1)确定被控模型
因式分解被控模型
2)考虑有无滞后环节
若控制系统中含有时滞环节,而时滞对于系统的控制运动具有一定的影响,因此在控制器设计中需将其考虑在内。控制器设计时将纯滞后环节进行近似处理,可采用一阶Pade逼近
3)滤波器设计
采用Ⅰ型IMC滤波器
采用Ⅱ型IMC滤波器
其中,λ为滤波器中的可调整时间常数。r的设计使控制器成为有理传递函数。滤波器f(s)直接影响系统的闭环性能,时间常数越小,f(s)对Y(s)的跟踪滞后越小。滤波器的另外一个重要作用是调整系统的鲁棒性,即时间常数Tf越大,系统鲁棒性越好。
2.3 非线性系统控制器设计在实际的工业控制中,大多数控制对象并非是单变量的线性模型,而是多种输入变量相互耦合的非线性模型,因此在进行内模控制时需求取系统逆模型和解耦,这增加了内模控制的复杂性。
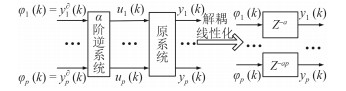
逆系统方法是一种通过反馈线性化处理非线性模型的解耦控制方法。系统的逆系统是指实现从原系统的输出到输入的系统。对于模型已知且相对精确的系统,通过数学推导方法可求的原系统的α阶逆系统,将α阶逆系统与原系统复合成为伪线性系统,对构造后的新系统即伪线性系统进行内模控制。基于逆系统方法的内模控制结构清晰,算法简单[6-7]。
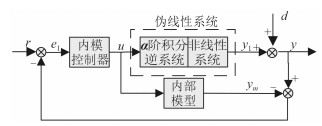
伪线性系统下内模控制的结构如图 4所示,其中,r为系统输入,d为系统扰动量,y为控制系统输出,ym为内部模型输出。经由逆系统和原系统构造后的新系统,模型简单,内模控制器设计容易方便,解决了原非线性系统的逆模型构造困难的问题[8-9]。
|
图 3 基于α阶逆系统的解耦线性化及α阶伪线性系统 Fig. 3 Based on the α-integral inverse system decoupling linearization and α-integral pseudo-linear system |
|
图 4 伪线性系统下内模控制 Fig. 4 Internal model control under the pseudo-linear system |
由原系统和其逆系统组合而成的复合系统称为伪线性系统,其复合后的新系统的输入和输出的关系是线性的,呈恒等映射关系。但复合系统的内部结构还可能是非线性的、耦合的。由逆系统和原系统组成的新系统可按照一般的线性控制方法进行控制,控制变得相对简单明了。
3 仿真实验及结果分析 3.1 仿真对象基于T. I. Fossen低频运动模型,一个与实际船舶按26:1比例缩小的2.8 m实验船舶低频下在静水中模型如下[10]:
| $ \left\{ {\begin{array}{*{20}{l}} {(m - {X_{\dot u}}) \cdot \dot u - {X_u} \cdot u \cdot \left| u \right| = {F_u}{\rm{, }}}\\ {\begin{array}{*{20}{l}} {(m - {Y_{\dot v}})\dot v - {Y_v} \cdot {v^3} + [(m \cdot {X_g}-{Y_{\dot r}})\dot r{\rm{, }}}\\ {-{Y_r} \cdot r] \cdot {\rm{sgn}}(v) = {F_v}{\rm{, }}} \end{array}}\\ {({I_z} - {N_{\dot r}})\dot r - {N_r} \cdot r = {F_r}{\rm{, }}} \end{array}} \right. $ | (13) |
式中:Fu,Fv,Fr分别为静水中船舶在横向、纵向的力和首向的转矩。
3.2 仿真参数通过参数理论计算结果+辨识结果,得到低频部分的参数如下:
| $ \begin{array}{*{20}{l}} {m - {X_{\dot u}} = 223.7, \;{X_u} = - 46.4, \;m - {Y_{\dot v}} = 90, }\\ {{Y_v} = - 450, \;m \cdot {X_g} - {Y_{\dot r}} = 75, \;{Y_r} = - 40, }\\ {{I_z} - {N_{\dot r}} = 150, \;{N_r} = - 45.} \end{array} $ | (14) |
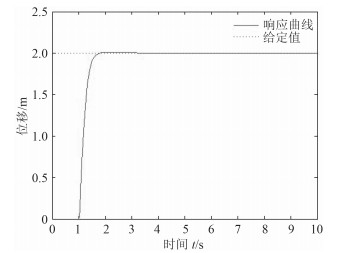
船舶的速度控制和位置控制均采用内模控制,在船舶纵向运动上,对采用逆系统方法构造的新系统进行船体运动控制和不加入逆系统进行船体运动控制的响应图分别如图 5和图 6所示。
|
图 5 引入逆系统系统响应 Fig. 5 Response of Introducing the inverse system |

|
图 6 无逆系统系统响应 Fig. 6 Response without the inverse system |
纵向位移设定值为2 m。系统不加入逆系统时,其控制器设计直接取模型的逆。从图中可看出,加入逆系统后的控制响应基本无超调,响应时间短。不引入逆系统的控制响应还存在一定的偏差。可以看出逆系统的引入对系统的控制效果有很大的提升。
3.4 控制器限幅下船舶运动仿真船舶在高海情下进行航向控制时,由于执行器物理特性的限制,会出现舵机速度饱和问题。如果设计船舶航向控制器时忽略舵机饱和问题,将导致闭环系统的性能下降,甚至导致系统不稳定[11]。
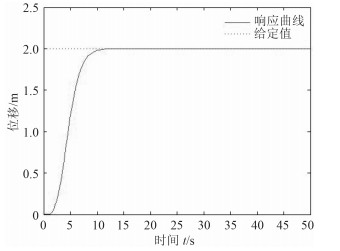
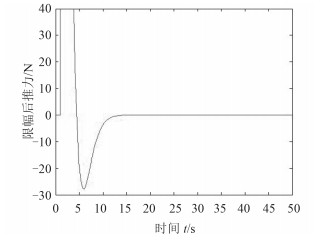
本文考虑在仿真中加入限幅环节,限幅值通过海洋工程重点实验室的船舶实际测量得到,纵向运动限幅值在-30~40 N,通过仿真得到限幅下双环内模的响应如图 7所示,有无引入限幅环节后的控制器的输出后的力的响应分别为图 8和图 9所示。
|
图 7 有限幅环节系统响应 Fig. 7 Response of controlled variable limitation |

|
图 8 限幅前控制器力的输出 Fig. 8 The force before control limitation |
|
图 9 限福后控制器力的输出 Fig. 9 The force after control limitation |
由上述3图可看出,加入限幅后,系统响应仍然满足要求,且能达到良好的效果。同时在没有限幅时力的输出要达到很大,但经过限幅后力以最大值输出,跳变不剧烈,能考虑到螺旋桨的改变能力,达到绿色控制。
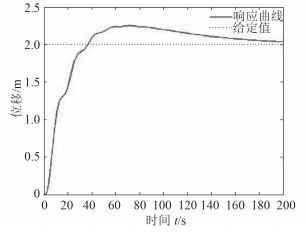
3.5 引入其他控制方法仿真效果对比PID控制器由于用途广泛、使用灵活。本文考虑在控制中引入PID控制[12]。船舶纵向运动双环控制均采用PID控制响应如图 10所示,内环控制采用PID控制且外环采用内模控制后响应如图 11所示。
|
图 10 双环pid响应仿真图 Fig. 10 Response of double-loop PID |
|
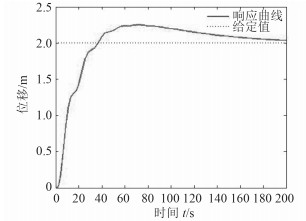
图 11 内环pid外环内模系统响应仿真图 Fig. 11 Response of PID and IMC |
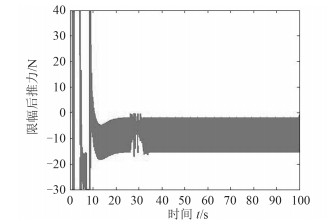
内环控制采用PID控制且外环采用内模控制,在对控制系统限幅后,控制器力的输出如图 12所示。
|
图 12 限福后控制器力的输出 Fig. 12 The force after control limitation |
由上述3图可以看出,双环pid超调大、响应时间长。内模与pid相结合的方法能良好的跟踪响应,但响应时间增加,同时经控制器输出的力出现了剧烈的跳变,这会对螺旋桨产生很大的压力,在实际中根本无法完成。由对比发现2种情况下的控制效果均达不到双层内模的控制效果。
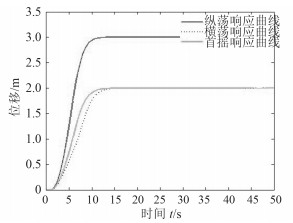
3.6 船舶运动仿真效果根据实际船舶模型,基于内模控制与逆系统算法对船舶进行纵荡、横荡、首摇的控制,纵荡、横荡、首摇设定值分别为3 m,2 m,2 rad,系统响应如图 13所示。
|
图 13 基于逆系统和内模算法的动力定位控制器响应仿真图 Fig. 13 Response of controller based on inverse system and IMC |
本文提出在船舶航向运动控制中引入内模控制法和逆系统法,同时提出设计一个双闭环的内模控制系统。经实际模型仿真实验,使用新方法的控制系统由于解决了模型非线性、控制量饱和等控制问题,再加上内模控制本身的一些控制优点,因此具有快响应、无超调、无静差等良好的控制效果。成功实现船舶运动良好的跟踪效果,降低了舵机的频繁操作,满足绿色控制的要求。
| [1] |
周涌, 陈庆伟, 胡维礼. 内模控制研究的新发展[J]. 控制理论与应用 , 2004, 21 (3) :475–482.
ZHOU Yong, CHEN Qing-wei, HU Wei-li. New developments of research on internal model control[J]. Control Theory & Applications , 2004, 21 (3) :475–482. |
| [2] | FOSSEN T I. Guidance and control of the ocean vehicles[M]. New York: Wiley, 1994 . |
| [3] | FOSSEN T I, PEREZ T. Kalman filtering for positioning and heading control of ships and offshore rigs: estimating the effects of waves, wind, and current[J]. IEEE Control Systems , 2009, 29 (6) :32–46. DOI:10.1109/MCS.2009.934408 |
| [4] |
陈庆伟, 吕朝霞, 胡维礼, 等. 基于逆系统方法的非线性内模控制[J]. 自动化学报 , 2002, 28 (5) :715–721.
CHEN Qing-wei, LV Zhao-xia, HU Wei-li, et al. Nonlinear internal model control based on inverse system method[J]. Acta Automatica Sinica , 2002, 28 (5) :715–721. |
| [5] | GARCIA C E, MORARI M. Internal model control. A unifying review and some new results[J]. Industrial & Engineering Chemistry Process Design and Development, 1982, 21(2): 308-323. |
| [6] |
宋夫华.支持向量机逆系统方法及其应用研究[D].杭州:浙江大学, 2006.
SONG Fu-hua. Study on support vector machine inverse system method and its application[D]. Hangzhou: Zhejiang University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10335-2006081147.htm |
| [7] |
宋夫华, 李平. 基于支持向量机α阶逆系统方法的非线性内模控制[J]. 自动化学报 , 2007, 33 (7) :778–781.
SONG Fu-hua, LI Ping. Nonlinear internal model control based on support vector machine α th-order inverse system method[J]. Acta Automatica Sinica , 2007, 33 (7) :778–781. |
| [8] |
李炜, 程应峰, 许德智. 基于逆系统多模型内模主动容错控制[J]. 计算机仿真 , 2011, 28 (3) :222–226.
LI Wei, CHENG Ying-feng, XU De-zhi. Active fault tolerant control using multi-model based on inverse system internal model[J]. Computer Simulation , 2011, 28 (3) :222–226. |
| [9] | KIM K K K, RÍOS-PATRÓN E, BRAATZ R D. Robust nonlinear internal model control of stable Wiener systems[J]. Journal of Process Control , 2012, 22 (8) :1468–1477. DOI:10.1016/j.jprocont.2012.01.019 |
| [10] | 王钦若, 刘芸, 彭义, 等.一种基于逆系统和内模控制的船舶动力定位控制方法: 201410163994.9[P]. 2014-11-12. |
| [11] |
宋佳, 刘胜, 李高云. 船舶航向最小二乘支持向量机内模控制[J]. 电机与控制学报 , 2009, 13 (S1) :183–187, 192.
SONG Jia, LIU Sheng, LI Gao-yun. LSSVM-IMC control for ship course-keeping system[J]. Electric Machines and Control , 2009, 13 (S1) :183–187, 192. |
| [12] | ZHAO Z C, LIU Z Y, ZHANG J G. IMC-PID tuning method based on sensitivity specification for process with time-delay[J]. Journal of Central South University of Technology , 2011, 18 (4) :1153–1160. DOI:10.1007/s11771-011-0817-0 |
 2016, Vol. 38
2016, Vol. 38
