近年来,水声与电子信息技术发展迅猛,利用舰船辐射噪声对目标进行识别的技术得到了极大关注,其无论在军事领域还是在民用领域,都具有十分重要的研究意义和应用价值。水文条件的变化、海洋环境噪声的干扰、海水的声吸收以及各种隐身技术的应用等因素导致舰船辐射噪声表现出非平稳、低信噪比的特点,这给水下目标识别造成了很大的困难。
水下目标辐射噪声信号去噪和特征提取是水下目标识别技术中的重要步骤,而基于传统傅里叶变换的信号处理方法不能很好地处理非平稳信号。近年来,小波分析方法在信号处理中得到了广泛应用,其在高频段具有低的频率分辨率和高的时间分辨率,在低频段具有高的频率分辨率和低的时间分辨率。小波分析的这种特性使其在处理时变、非平稳信号具有明显的优势。
目前,基于小波去噪的算法中常用的是Donoho提出的阈值去噪法,该方法的降噪效果好,降噪原理简单且易于实现。许多学者将小波分析应用到舰船辐射噪声的特征提取中,提出基于小波变换的能量特征提取方法,但该方法大多采用的是具有平移敏感性的离散小波变换,导致提取的特征不够稳定[1]。Kingsbury等[2]提出的双树复小波变换(Dual-Tree Complex Wavelet Transform,DT-CWT),具有近似平移不变性,克服了传统离散小波变换的缺点,且算法成熟,能够更好地提取信号特征。
本文对舰船辐射噪声信号的降噪与特征提取问题进行探讨。首先,对基于小波阈值降噪的方法进行研究,采用一种新的阈值函数,得到了更好的降噪效果;其次,将双树复小波变换应用到舰船辐射噪声特征提取,得到了稳定的目标特征向量。通过仿真数据与实航数据分析,验证了方法的有效性。
1 小波阈值降噪及其原理小波阈值降噪是目前较为常用的一种去噪方法,其基本原理如下[3]:小波变换具有去相关和能量压缩的特性,能够将真实信号的能量集中在少数稀疏的、幅度较大的小波系数上,而白噪声的小波变换仍然是白噪声,它广泛分布在各个尺度的小波系数上,且值较小。
一维信号的小波阈值去噪主要有以下3步:
1)选择合适的小波并确定小波分解的层次N,对信号进行N层小波分解;
2)对从第1层到第N层的每一层高频系数,选择一个阈值进行阈值量化处理;
3)根据小波分解第N层的低频系数和经过量化处理后的第1层到第N层的高频系数,对一维信号进行小波重构。
在上述步骤中,阈值的选取和量化最为关键。根据文献[4],本文选取的阈值计算公式如下:
| $ t{h_j}={\sigma _{n, j}}\sqrt {2 \cdot \ln(\frac{N}{{{2^j}}})}, {\sigma _{n, j}}=\frac{{Median\{ |{\upsilon _{j, n}}|\} }}{{0.6745}}. $ |
式中:thj 为小波变换后j层小波系数的阈值。
小波阈值施加有硬阈值和软阈值2种方式,硬阈值法直接将高频的小波系数直接置0,很可能把有用的高频特征信号消除,因此在降噪中,常用软阈值法,当小波系数小于阈值时,不是简单的置0,而是平滑地减小到0。阈值函数的选取应满足2个条件:使估计的小波系数与原始信号小波系数接近;使信号在小波域连续。本文采用一种新的阈值函数[5]:
| $ \eta(x, th, m)=\left\{ \begin{array}{l} x - 0.5 \cdot th \cdot {\rm{sign}}(x)|x| > th, \\ 0.5 \cdot k \cdot th \cdot \tan(\frac{{{\rm{\pi }} \cdot x}}{{4 \cdot th}})|x| \le th. \end{array} \right. $ | (1) |
式中:th为阈值,k为可调节的实数。
选择仿真信号为正弦信号加高斯白噪声,对该方法进行检验,正弦信号为:
| $ f(n)=\sum\limits_{i=8}^{11} {\sin(2 \cdot {\rm{ \pi }} \cdot i \cdot n/220)} {\mkern 1mu} {\mkern 1mu} {\rm{.}} $ | (2) |
信噪比为0 dB,将该方法与Mtalab自带的经典的小波阈值降噪算法进行对比,都使用sym3作为小波基,分解层数为3层,降噪结果如表 1所示。
|
|
表 1 降噪结果对比 Tab.1 Noise reduction results comparison |
从表 1可看出,本文方法的信噪比更高,降噪效果优于其他方法。
2 基于双树复小波变换的能量特征提取水下目标辐射的噪声或者经同一发射信号激发的水下目标回波,所包含的能量频谱分布与目标的大小、形状和类型密切相关[6] 。因此,可以将舰船辐射噪声的能量谱分布作为目标识别的特征。
传统离散小波变换在二抽取过程中会产生混叠,混叠导致离散小波变换对信号的平移十分敏感。平移敏感性是指输入信号一个很小的平移会使小波系数产生非常明显的变化。虽然小波滤波器组能够保证信号完美重构,或者说低通和高通分量的总能量对于信号平移能够保持不变,但是低通和高通分量却不能单独保持平移不变[7-8] 。
利用双树复小波变换进行特征提取的步骤如下:
1)对原始信号进行双树复小波分解,得到各层信号的小波系数;
2)对高频的小波系数进行重构,得到重构的各层信号;
3)求高频各层信号的能量Ei(i=1, 2, ...),其中
式中Sj (k)(j≥1)为分解得到的第j层高频信号的第k个点;
4)构造特征向量。
| $ \text{特征向量}\quad { \boldsymbol{T}}=\left[{\frac{{{E_1}}}{E}, \frac{{{E_2}}}{E}, \frac{{{E_3}}}{E}, \frac{{{E_4}}}{E}, ...} \right] \text{,} $ | (5) |
其中:
为了对上述方法进行验证,本文对仿真信号和实测数据进行处理。
3.1 实验仿真舰船辐射噪声由线谱形式的单频噪声和具有连续谱的宽带噪声组成,舰船辐射噪声线谱的仿真方式如下[9]:
| $ {s_i}(n)=\sum\limits_{k=1}^{{K_i}} {{a_{ik}}\sin } \left\{ {{k_i}\left[{2{\rm{\pi }}{f_i}n{T_s}+{\varphi _i}(n)} \right]+{\gamma _{ik}}} \right\}. $ | (4) |
式中:Ki 为第i组谐波分量所含的谐波数;γik 为均匀分布在[0,2π]的随机量;φi (n)为随机漂移相位;Ts 为采样时间间隔。
宽带连续谱采用白噪声通过一个具有指定幅频响应的滤波器来模拟。
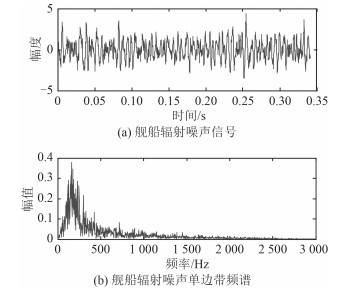
图 2是根据上述方法产生的舰船辐射噪声信号及其频谱;仿真信号的采样频率为6 kHz,长度为2 048点,信噪比为-3 dB。
|
图 1 仿真的舰船辐射噪声信号及其频谱 Fig. 1 Simulation of ship radiated noise and its spectrum |
|
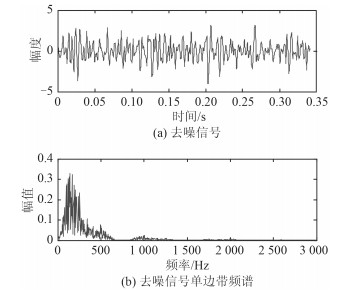
图 2 去噪后的舰船辐射噪声信号及其频谱 Fig. 2 Ship radiated noise and its spectrum after noise reduction |
从图 2可看出,去噪后的信号更加平滑,消除了大部分高频分量。
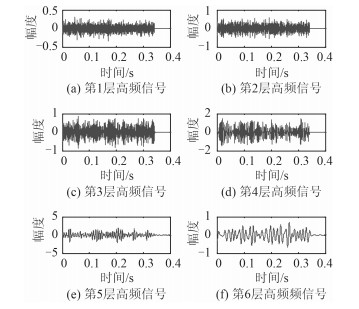
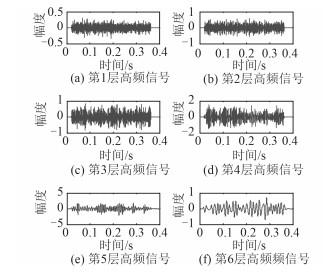
对原始的舰船辐射噪声和时移125点后的舰船辐射噪声信号分别6层进行双树复小波变换和离散小波变换得到相应的小波系数,根据高频部分的小波系数重构出的各层高频信号如下:对比平移前后双树复小波变换的结果与离散小波变换的结果,从时域上看,信号平移前后双树复小波变换重构的各层信号基本没有发生改变,而使用离散小波变换重构的信号变化较大。
从表 2可看出,使用双树复小波变换处理平移前后的信号,重构的各层信号能量基本不变,但是使用实小波变换重构的第3,4,5层高频信号的能量,平移前后所得结果有较大变化。因此,利用双树复小波变换重构所得各层信号的能量更加稳定。
|
|
表 2 各层高频信号能量对比 Tab.2 Energy contrast of different frequency signals in different layers |
对实测的某船只的舰船辐射噪声进行处理,该数据的采样频率为10 kHz,将同一段数据分别进行20次平移,平移的间隔为1个采样点。对这20段不同长度的平移信号和原始信号分别利用本文方法和传统基于离散小波的方法计算其特征向量,并将2组特征向量绘制成图,如图 7~图 8所示。
|
图 3 原始信号的双树复小波重构信号 Fig. 3 Reconstruction signals of original signal using DT-CWT |

|
图 4 原始信号的离散小波变换重构信号 Fig. 4 Reconstruction signals of original signal using DWT |
|
图 5 时移信号的双树复小波变换重构信号 Fig. 5 Reconstruction signals of shifted signal using DT-CWT |
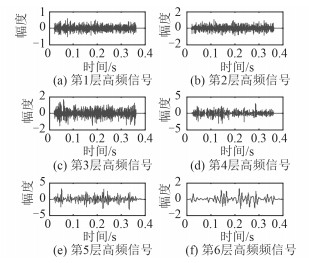
|
图 6 时移信号的离散小波变换重构信号 Fig. 6 Reconstruction signals of shifted signal using DT-CWT |
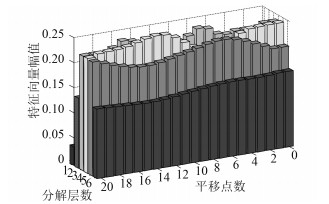
|
图 7 不同时移信号的特征向量(离散小波变换) Fig. 7 Feature vectors of different shifted signals using DWT |
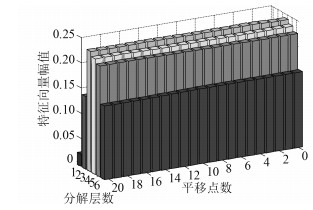
|
图 8 不同时移信号的特征向量(双树复小波变换) Fig. 8 Feature vectors of different shifted signals using DT-CWT |
从图中可以看出,不同时移情况下,利用双树复小波变换所得特征向量基本没有发生变化,而利用离散小波变换所得的特征向量发生了明显的波动,这说明本文提出的方法能够提取稳定的目标特征。
4 结语本文在小波阈值降噪方法中使用了一种新的阈值函数,得到了较好的去噪效果;将双树复小波变换应用到舰船辐射噪声的能量特征提取中,从仿真试验和实航数据验证中可以看出,其特征向量基本不随信号的时移而发生改变,结果具有较好的稳定性。
| [1] | 徐慧.水声目标被动识别相关技术研究[D].武汉:武汉教育工程研究院, 2013. |
| [2] | SELESNICK I W, BARANIUK R G, KINGSBURY N G. The dual-tree complex wavelet transform[J]. IEEE Signal Processing Magazine , 2005, 22 (6) :123–151. DOI:10.1109/MSP.2005.1550194 |
| [3] | 胡广书. 现代信号处理教程(2版)[M]. 北京: 清华大学出版社, 2015 : 380 -388. |
| [4] | DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory , 1995, 41 (3) :613–627. DOI:10.1109/18.382009 |
| [5] | 王遥遥.基于小波理论的信号降噪方法的研究[D].武汉:武汉理工大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10497-1013296515.htm |
| [6] | 张静远, 张冰, 蒋兴舟. 基于小波变换的特征提取方法分析[J]. 信号处理 , 2000, 16 (2) :156–162. |
| [7] | 苏文胜.滚动轴承振动信号处理及特征提取方法研究[D].大连:大连理工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10141-2011013973.htm |
| [8] | 石宏理, 胡波. 双树复小波变换及其应用综述[J]. 信息与电子工程 , 2007, 5 (3) :229–234. |
| [9] | 邢国强, 孙超, 唐建生, 等. 典型舰船辐射噪声的时域模拟[J]. 鱼雷技术 , 2005, 13 (4) :41–43. |
 2016, Vol. 38
2016, Vol. 38
