0 引言

航空发动机管路是指由管路将发动机各部件之间相互连接，输送各自规定液体的通道^[1]。根据对管路断裂的统计分析，90%的断裂属于损伤破裂，与充液过程中管路自身的振动造成有关^[2]。航空动力系统的故障多是由管路的破裂所引起，而管路振动是导致破裂发生和裂纹延续的主要原因^[3]，所以研究供油管路的振动很有必要。

对于充液管路的振动已经有许多学者开展了此方面的研究。最开始源于经典的水击理论，而经典水击理论只考虑管壁弹性对管内液体压力波的影响，而未考虑流固耦合之间的相互作用。当管路中液体流速、压力突然改变或者管路系统中的机械不规则振动发生时，都会诱发液体的脉动，进而造成管路振动。对于单管路的流固耦合振动是通过有限元仿真计算软件实现的。Karl Kuehlert^[4]模拟研究得到了振动频率和幅值，并与实验结果进行对比；郭庆^[5]模拟了在给定的流速脉冲和不同支撑方式下的管路动力学响应；梁建术^[6]仿真了节流孔板对输液管路系统的振动控制；彭先勇^[7]对载流管路振动进行仿真分析，并通过实验进行验证；杨莹^[8]对航空发动机管路的流固耦合振动进行分析，讨论了管内液体质量、压力、温度，管路形状、截面尺寸对管路流固耦合固有频率的影响。

本文以线性充液管路为研究对象，在有限元软件Ansys中进行卡箍限振状态下的模拟分析，计算模态频率和振型，为卡箍的布局提供理论基础和参考价值。

1 有限元模型

由于充液管路是液体与固体之间的相互作用，即液体振动引发固体振动，固体振动反过来又影响液体振动。因此需考察液体的连续相湍流模型和固体管路力学位移模型。

1.1 液体连续相湍流模型

连续性方程为：

$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}} = 0,$

式中：ρ为流体密度，u为流体相速度。

动量方程为

$ \begin{array}{l} \displaystyle\frac{{\partial (\rho {u_i})}}{{\partial t}} + \frac{{\partial ({u_i}{u_j})}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}[\mu (\frac{{\partial {u_i}}}{{\partial {x_j}}} + \\ \quad \quad \quad \displaystyle\frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_k}}}{{\partial {x_k}}})] + \frac{\partial }{{\partial {x_j}}}( - \rho \overline {{{u'}_i}{{u'}_j}} )\text{，} \end{array} $

式中：i，j，k为三维坐标系中的坐标方向；μ为流体动力粘度；δ_ij为单位张量。

雷诺应力 $ - \rho \overline {{{u'}_i}{{u'}_j}} $ 采用Boussinesq假设，为：

$ - \rho \overline {{{u'}_i}{{u'}_j}} = {\mu _t}(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}) - \frac{2}{3}{\delta _{ij}}(\rho k + {\mu _t}\frac{{\partial {u_k}}}{{\partial {x_k}}})\text{，} $

标准k-ε模型及其湍动能和耗散率方程如下：

$ \begin{aligned} & \displaystyle \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_j}}}[(u + \frac{{{u_t}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial {x_j}}}] + \\ & \quad \quad \quad {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k}\text{，}\\ & \displaystyle \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {x_i}}}(\rho \varepsilon {u_i}) = \frac{\partial }{{\partial {x_j}}}[(u + \frac{{{u_t}}}{{{\sigma _\varepsilon }}})\frac{{\partial \varepsilon }}{{\partial {x_j}}}] + \\ & \quad \quad \quad {C_{1\varepsilon }}\frac{\varepsilon }{k}({G_k} + {C_{3\varepsilon }}{G_b}) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon }\text{。} \end{aligned} $

式中：G_k为由于平均速度梯度引起的湍动能产生；G_b为由于浮力影响引起的湍动能产生；Y_M为可压缩湍流脉动膨胀对总耗散率的影响；C_1ε，C_2ε，C_3ε为经验常数；σ_k，σ_ε为湍动能和湍动耗散率对应的普朗特数。

1.2 固体管路力学位移模型

有限元理论是以离散元为基础，首先要将管路理想化为简单结构元素的组合，各元素仅在其共同的各节点相互连接，由经典理论力学方程可知各节点的位移和作用在各节点上外力之间有着如下关系式：

$$\mathit{\boldsymbol{M}}x'' + \mathit{\boldsymbol{C}}x' + \mathit{\boldsymbol{K}}x = \mathit{\boldsymbol{F}}(t),$$

其中，M为各个节点的质量矩阵；C为各个节点的阻尼矩阵；K为各个节点刚度矩阵；x，x′和x″分别为节点位移向量、速度和加速度；F（t）为随时间变化的节点载荷矩阵。

1.3 耦合控制流程

流体方程与结构方程在求解时是按照一定的顺序相互迭代来求解，将各自每一步算到的结果传到另一部分继续用来计算，只有使耦合系统的解成为收敛的才可以结束迭代。所以说这样才能使流体和结构的求解变量完全耦合。

想要得到t+∆t时刻的解，就要在流体模型和结构模型之间展开迭代计算。设初始解为 $\mathop {\mathop d\nolimits_s }\nolimits^{ - 1} = \mathop {\mathop d\nolimits_s }\nolimits^0 = {}^t\mathop d\nolimits_s ,\mathop {\mathop \tau \nolimits_s }\nolimits^0 = {}^t\mathop \tau \nolimits_s $ ，对迭代步k=1，2，3…，进行下面的求解过程以得到解 ${}^{t + \Delta t}X$ 。

1）从流体方程 $\mathop F\nolimits_f \left[ {\mathop X\nolimits_f ,\mathop \lambda \nolimits_d \mathop {\mathop d\nolimits_s }\nolimits^{k - 1} + \left( {1 - \lambda } \right)\mathop {\mathop d\nolimits_s }\nolimits^{k - 2} } \right] = 0$ 中得到流体解向量 $\mathop {\mathop X\nolimits_f }\nolimits^k $ 。运用给定的结构位移对流体模型求解才可以得出这个解。但计算中还需要观察到的是结构的位移运用了位移松弛因子 $\mathop \lambda \nolimits_d \left( {0 < \mathop \lambda \nolimits_d < 1} \right)$ ，因为流体和结构2个模型不在一个矩阵中求得解，所以像这样的处理会在做一些比较麻烦且繁杂的模型时会产生很好的帮助效果。迭代形成了收敛是因为有了松弛因子的帮助。

2）若只需要满足应力收敛条件，那么就要计算应力残量并和迭代容差做比较。若是将这个标准达到，那么就可以不再进行步骤3~步骤5。

3）从结构方程 $\mathop F\nolimits_s \left[ {\mathop {\mathop X\nolimits_s }\nolimits^k ,\mathop \lambda \nolimits_\tau \mathop {\mathop \tau \nolimits_f }\nolimits^{k - 1} } \right] = 0$ 中解出结构解向量 $\mathop {\mathop X\nolimits_s }\nolimits^k $ 流体应力同样运用了应力松弛因子 $\mathop \lambda \nolimits_\tau \left( {0 < \mathop \lambda \nolimits_\tau < 1} \right)$ 。

4）流体的节点位移要用给定的边界条件 $\mathop {\mathop d\nolimits_f }\nolimits^k = \mathop \lambda \nolimits_d \mathop {\mathop d\nolimits_s }\nolimits^k + \left( {1 - \mathop \lambda \nolimits_d } \right)\mathop {\mathop d\nolimits_s }\nolimits^{k - 1} $ 计算。

5）假如说只满足位移收敛条件这一个条件，那么就要计算位移残量并和迭代容差做比较。当应力和位移的标准都要求满足时，则2个收敛条件都要检查。如果迭代不收敛，回到步骤1）继续下一个迭代，直到达到FSI迭代的最大数（这种情况下，程序停止，显示不收敛信息）。

6）保存而且输出流体和结构的结果。时间步和求解时间在这种解法当中是由流体模型所操控。但是，结构模型中定义的所有时间函数必须覆盖计算的时间范围。在耦合系统中，流体模型决定了这些控制收敛的参数，如应力和位移迭代容差、松弛因子、收敛标准等。

2 充液管路三维模态分析

按照与实际无阻尼自由振动管长1 000 mm，直径18 mm，管子壁厚1 mm的比率建立模型，并划分网格，如图 1所示，参数设置如表 1所示。

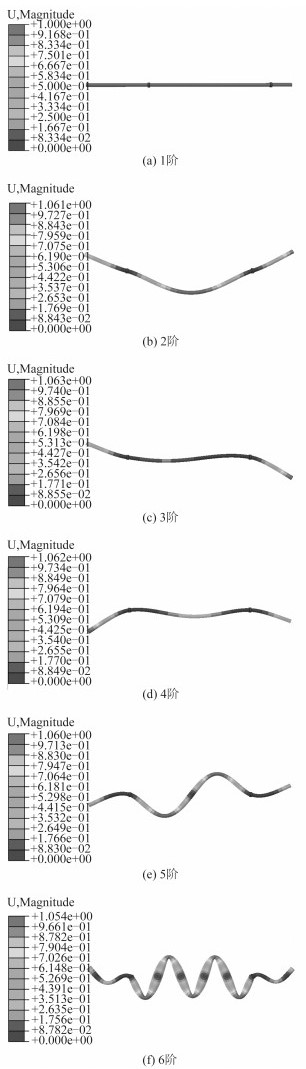
对充液管路施加对称卡箍布置，并对管路进行6阶模态分析，得到模拟清单（见表 2）和等效位移模态结果（见图 2），分析可知卡箍布局处明显减弱了振动的效果，以卡箍布局点为中心，越远离振动效果越明显。随着振动频率的增加，共振情况明显得到加强，但特征值并没有随之增大，这正是卡箍限制的缘故，所以在充液管路上设置卡箍是减弱振动很有必要的一种手段。

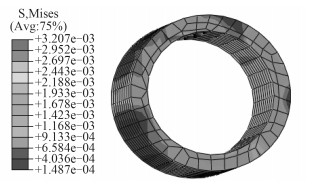
振动会引起内部应力的变化，应力才是导致破裂的原因，于是跟中管路中间点，图 3为液固耦合作用下管路中点的Von Misses应力云图。有图可知产生应力的变化近似于均匀分布，应力最大点发生在管子内部。引发共振时，这些点呈现无规则的跳动，所以在生产充液管路的时候需要加强对其内表面的处理。

3 充液管路长度对压力波动的影响

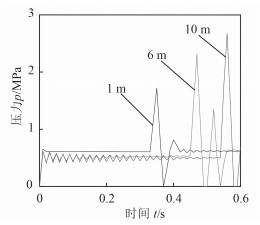
经计算满足该系统工作条件的充液管路的最小内径为16 mm，根据在实际应用中所选充液管路的最小内径应该稍大于系统所需的最小内径的原则，再次选择充液管路直径18~26 mm的条件下，分析连接充液管路的长度分别为1 m、6 m、10 m时管子出液端的压力变化情况，如图 4所示。可知：压力变化是液压作用的宏观表现，波动的曲线反应出充液过程是一个复杂的作用过程。充液管路越长波动的趋势越不明显，这是因为波动沿着管路进行衰减，充液管路越长衰减越明显。

表 3给出了不同充液管路长度下的制动峰值，可以看出在连接管径大小确定的情况下，油缸充液管路出口的压力峰值会逐渐增加，但是相对于长度增加的幅度来说并不明显。所以连接充液管路的长度对于降低系统的压力峰值并没有显著的作用。因此在选择连接管径的长度时应根据液压系统的布置情况和降低成本的原则，尽量选择布置长度较短的充液管路。

4 结语

本文以线性充液管路为研究对象，对卡箍限对称布局限制下的管路振动情况进行了有限元模拟分析，并分析了充液管路长度对压力波动的影响，研究了充液管路的振动模态及Von Misses应力分布。研究得到卡箍布局处明显减弱了振动的效果，以卡箍布局点为中心，越远离振动效果越明显。随着振动频率的增加，共振情况明显得到加强。应力的变化近似于均匀分布，应力最大点发生在管子内部。这对后期的卡箍布局减振设计具有重要的理论意义。压力变化是液压作用的宏观表现，波动的曲线反应出充液过程是一个复杂的作用过程，尽量选择布置长度较短的充液管路。