0 引言

自吸离心泵主要通过改变泵体结构使其具有抽真空能力（自吸能力），比如气液混合式自吸泵。根据液体和气体在泵中混合位置的不同，气液混合式自吸泵分为内混式和外混式^[1-2]。本文所研究的对象为船用某型外混式自吸泵。

在借助UG建立该泵三维实体模型的基础上，通过HyperMesh进行模型主要结构网格划分和分析条件设置；利用Ansys Mechanical APDL对模型进行求解设置，完成模态计算并对结果进行分析。

1 理论基础

在动力学分析中，对于一个无阻尼自由振动自由度为的线性系统，运动微分方程为^[3]：

$$\mathit{\boldsymbol{M\ddot u}} + \mathit{\boldsymbol{Ku}} = 0,$$

(1)

式中：M和K分别为系统的质量和刚度矩阵；ü和u为系统各节点的加速度和位移向量。

式（1）的解可表示为：

$$\mathit{\boldsymbol{u}} = \mathit{\boldsymbol{\varphi }}{e^{j\omega t}} 。 $$

(2)

式中：ω为简谐振动圆频率；φ为节点振幅列向量； $$\varphi = \left\{ {{\varphi _1},{\varphi _2},...,{\varphi _n}} \right\};{\mathit{\boldsymbol{\varphi }}_i}$ 为自由度i方向上的振幅。将式（2）代入式（1）并消去 ${e^{j\omega t}}$ ，得^[4]：

$$\left( {\mathit{\boldsymbol{K}} - {\omega ^2}\mathit{\boldsymbol{M}}} \right)\mathit{\boldsymbol{\varphi }} = 0,$$

(3)

在自由振动时，系统中各节点的振幅φ不全为0，由此可得^[4]：

$\left| {\mathit{\boldsymbol{K}} - {\omega ^2}2\mathit{\boldsymbol{M}}} \right| = 0。$

(4)

因为M和K都是n阶方阵，所以式（4）是关于ω²的n次实系数方程。可以从中解出n个实根 $\omega _i^2\left( {i = 1,2, \ldots ,n} \right)$ ，即特征值。把任一 $\omega _i^2$ 代回式（3），可解出与其相对应的向量 $${\mathit{\boldsymbol{\varphi }}_1},{\mathit{\boldsymbol{\varphi }}_2}, \ldots ,{\mathit{\boldsymbol{\varphi }}_n}$ （i=1, 2, …n），即特征向量。其中特征值的平方根 ${\omega _1},{\omega _2}, \ldots ,{\omega _n}$ 分别为系统的1阶、2阶、…、n阶固有频率，与之对应的 $${\mathit{\boldsymbol{\varphi }}_1},{\mathit{\boldsymbol{\varphi }}_2}, \ldots ,{\mathit{\boldsymbol{\varphi }}_n}$ 分别是系统的各阶固有振型。

2 模型有限元前处理 2.1 模型简化

自吸泵模型主要由泵体、叶轮、泵盖、托架和轴构成。泵体等零部件上存在较多的螺纹孔和小倒角等结构。这些结构对模态分析结果影响较小，但在网格划分时却需要许多单元来模拟，增加运算量和计算时间^[5]。因此需要进行简化，删除模型中的螺纹孔（M < 15），通孔（Φ < 15 mm），倒角（尺寸 < 6 mm）、圆角（R < 6 mm）等微小结构。图 1为精简前后的模型。

2.2 模型网格划分

网格划分时，考虑到泵盖、托架和轴属于轴对称结构，可利用其结构的对称性经reflect命令完成六面体网格的划分。对于像泵体和叶轮这样具有复杂曲面的部件，采用四面体网格进行划分。其中泵体网格尺寸为5 mm，其余结构网格尺寸为3 mm。

2.3 条件与约束设置

设置模型接触并添加必要的约束，模型中主要的装配形式均为法兰盘螺栓装配。因此在Contact Manger中设置接触对为TARGET170和CONTA173。对于有约束的结构，施加dof1，dof2及dof3约束。

3 计算模态分析 3.1 主要零部件模态分析

将完成的有限元模型导入至Ansys Mechanical APDL，设置分析类型（Modal）、模态提取方法^[6]（Block Lanczos）、模态提取阶数（自由模态为16阶、约束模态为10阶）等参数，进行分析计算。通过计算，得到主要零部件前8阶的模态频率数据，如表 2所示。

该泵的电机型号为Y132S2-2H，额定转速为2 950 r/min，激励频率为2 950 ÷ 60=49.17 Hz；叶片通过频率为49.17 × 6=295 Hz，6为泵的叶片数。在分析计算时，要特别注意以上2个频率附近的振动情况^[7]。

表 2数据表明：

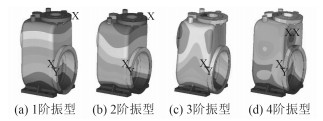
图 2表明：泵体以上半部分的摆动为主，伴随着部分挤压和扭转变形。其中1阶和2阶模态频率较低，且与叶片通过频率较为接近；3阶时，扭转变形更为明显，最大变形出现在泵入口及泵体顶角附近，属于异常变形，说明该处结构最为薄弱，这种变形对入口管路影响较大；4阶时，除泵体扭转变形之外，泵体中间部分还发生了挤压变形。

3.2 自吸泵装配体模态分析

为了进一步掌握泵整体的振动和变形情况，将泵的各零部件装配后，形成装配体，通过实际运行中的约束状态来分析装配体的模态信息。通过计算，得到装配体前8阶约束模态频率和前4阶振型图，分别如表 3和图 3所示。

对比分析表 2和表 3发现：装配体的模态频率要明显大于约束状态下泵体的模态频率，可见装配体的动态性能优于约束状态下的泵体，说明该泵的装配工艺较为合理。1阶和2阶模态频率主要集中在500~600 Hz之间，振型以上半部分的摆动为主，与泵体的前2阶约束模态基本相同。3阶和4阶模态振型显示装配体整体结构的薄弱环节出现在泵入口以及与之相邻的顶角处，但此时的模态频率与激振频率相差较大，不会引起结构共振。

4 结语

1）除泵体约束状态以外，自吸泵的主要零部件均有较高的模态频率，明显高于电机的激振频率及叶片通过频率，说明零部件具有较高的刚度。

2）在实际工作状态下，受约束的影响，泵体的动态性能有所降低，发生共振的可能性较高。泵体在入口、顶角和蜗壳出口附近存在异常变形，有必要对其进行加固。

3）装配体的模态频率要明显大于约束状态下泵体的模态频率，因此，在约束状态下，装配体的动态性能要明显优于单独的泵体，说明该泵的装配工艺较为合理，可以改善泵的动态性能。

4）装配体的振型以泵体的变形为主，并且与约束状态下的泵体振型相近。泵体结构中存在薄弱之处，有必要根据振型对该泵结构做针对性优化。