0 引言

畸形波是海洋中高且陡的大波，其持续时间很短，但出现的偶然性和巨大的破坏性对船舶航运和海洋工程结构物等极具威胁^[1]，因此畸形波越来越引起人们的关注，它的发生机理及工程应用问题已成为当前物理海洋学界和船舶水动力学界的一个研究热点问题。

畸形波的数值模拟主要有线性方法和非线性方法两种。畸形波模拟的非线性方法比较多见，大多数是基于非线性薛定谔方程来模拟畸形波。张运秋^[5]基于修正的四阶非线性薛定谔（mNLS）方程及伪谱数值方法建立了非线性波浪数值模型，模拟了边带扰动条件下和随机波条件下畸形波的生成，取得了较好的模拟效果。

线性理论方面，多基于Longuet-Higgins模型^[1]。黄国兴^[2]采用人工干预组成波的随机初相位的方法得到包含畸形波的波列，但模拟效率比较低，而且不能控制畸形波生成的时间和地点。Kriebel^[3]采用一个基本随机波列和一个瞬态波列线性叠加的双波列叠加模型模拟了畸形波；裴玉国^[4]采用改进的双波列叠加模型--三波列叠加模型优化了畸形波的模拟。但这2种模拟方法都基于瞬态波列，瞬态波列的能量所占的比例会影响整个模拟波列的谱的结构。

近年来，一些学者通过相位调制方法，在畸形波的数值模拟研究取得新进展。刘赞强^[6]采用改进的相位调制方法来模拟畸形波，既满足波浪序列的统计特性又可保持目标谱的结构，且模拟效率较高，是一种有效的模拟畸形波的方法。张本辉^[7]在相位调制生成畸形波的同时考虑了舰船航速航向的影响，可以对舰船在斜浪航行态势下定时定点遭遇畸形波的非线性波浪环境进行数值建模。然而，这些数值模拟采用的靶谱都是频谱，模拟的是长峰非规则波。而实测数据表明，现实的海浪多是短峰非规则波。因此本文研究以相位调制为手段，在Matlab语言环境下实现短峰畸形波的生成。

1 波浪数学模型

海浪是自然界中一种随机现象，由于影响波浪的因素很多，而且相互关系非常复杂，即使在同一条件下，其呈现的波浪也不完全确定。对于这种随机现象，欲寻找在某一时刻、一定地点波浪具体的特征值是不可能的，也无意义。但人们通过对海洋波浪的大量观测，发现这一表面看起来极不规则的随机波浪，实际存在着一定的规律性。波浪理论的发展经历了从复杂到简单，再从简单到复杂的过程。人们统计海浪的波高周期等特征，采用单一频率单一方向的波浪来表征特定情况的海浪，这样做使得各种影响因素独立清晰，易于分析各因素间的相互作用。随着研究手段的日益发展及不断出现的工程问题，使学者们逐步用单方向不规则波和方向谱不规则波来模拟海浪，进行工程应用和基础理论研究。

1.1 规则波

在流体力学研究中，有多种形式的波浪模型，本文采用耐波性水池实验中常用的平面进行波模型，也称之为微幅波（Airy wave）模型。规则波的波高及速度方程为：

$\eta {\rm{ = }}A\cos \left( {\omega t} \right),$

(1)

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} u = A\omega {e^{kz}}\cos (kx - \omega t){\rm{,}}\\ v = 0{\rm{,}}\\ w = A\omega {e^{kz}}\sin (kx - \omega t) 。 \end{array} \end{array}} \right.$

(2)

式中：η为波高；A为波幅；k为波数；ω为波浪圆频率。

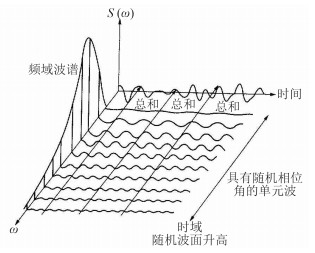
1.2 长峰不规则波

根据线性叠加原理，长峰不规则波可简化为同一方向上无数个不同波幅、不同频率和随机初始相位的单元规则波线性叠加而成，各成分波的能量分布如图 1所示，其波面及速度方程为：

$\eta = \sum\limits_{i = 1}^n {{A_i}\cos ({k_i}x + {\omega _i}t + {\varepsilon _i})} ,$

(3)

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} u = \sum\limits_{i = 1}^n {{A_i}{\omega _i}{e^{{k_i}z}}\cos ({k_i}x + {\omega _i}t + {\varepsilon _i})} {\rm{,}}\\ v = 0{\rm{,}}\\ w = \sum\limits_{i = 1}^n {{A_i}{\omega _i}{e^{{k_i}z}}\sin ({k_i}x + {\omega _i}t + {\varepsilon _i})} 。 \end{array} \end{array}} \right.$

(4)

设波浪谱S（ω）的能量绝大部分分布在ω_L~ω_H范围内，其余部分可根据精度要求进行取舍。频率等分法是指在所取得频率范围划分为N个区间，其间隔为∆ω=ω_i~ω_i-1，设子波波高在取∆ω区间内不变且相等，则取

$\begin{array}{*{20}{l}} \begin{array}{l} \hat \omega = ({\omega _{i - 1}} - {\omega _i})/2,\\ {A_i} = \sqrt {2{S_\eta }(\hat \omega )\Delta \omega } 。 \end{array} \end{array}$

1.3 短峰不规则波

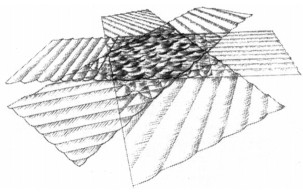
实际海面呈现的多为短峰不规则波，即波浪的方向是多向的，在时间上和空间上均不规则^[8]。短峰不规则波可以看作是由多个频率不等、方向不同、振幅变化且相位随机的微幅简谐波叠加而成的不规则波系，如图 2所示。

在空间位置（x，y）处，将多个振幅、频率、方向、相位不同的微幅波线性叠加起来，则t时刻的波面高度可表示为：

$\eta = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {{a_{ij}}\cos ({k_i}x\cos {\theta _j} + {k_i}y\sin {\theta _j} - {\omega _i}t + {\varepsilon _{ij}})} } 。 $

(5)

这就是短峰波的波面方程。其中：对于第i个频率、第j个方向的成分波而言，a_ij为波幅、ε_ij为随机相位；ω_i和k_i分别为第i个频率的成分波的圆频率和波数；θ_j为波浪沿x，y平面传播并与x轴所成的夹角。方向谱谱密度函数S（ω，θ）与波幅满足下列关系：

$\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\frac{1}{2}} } a_{ij}^2 = \int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {\int_0^\infty {S(\omega ,\theta )} } {\rm{d}}\omega {\rm{d}}\theta 。 $

(6)

方向谱还可表述为海浪频谱S（ω）和方向扩散函数D（ω，θ）的乘积：

$S(\omega ,\theta ) = S(\omega )D(\omega ,\theta ) 。 $

(7)

其中$\int\limits_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {D(\omega ,\theta )} {\rm{d}}\theta = 1$，D（ω，θ）的一般形式为：

$D(\omega ,\theta ) = {k_n}{\cos ^n}\theta (\left| \theta \right| \le \frac{{\rm{ \mathsf{ π} }}}{2}) 。 $

(8)

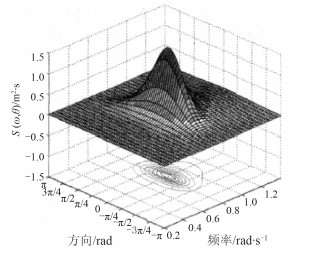
用方向谱来描述组成波的不同方向分布，如图 3所示。

国际船舶结构会议（ISSC）建议采用以下2种n值：

$\begin{array}{*{20}{l}} \begin{array}{l} n = 2,\quad {k_2} = 2/{\rm{ \mathsf{ π} ,}}\\ n = 4,\quad {k_2} = 8/\left( {3{\rm{ \mathsf{ π} }}} \right) 。 \end{array} \end{array}$

本文采用第1种形式进行建模，即n=2，${k_2} = 2/{\rm{ \mathsf{ π} }}$。

2 基于方向谱的相位调制技术

刘赞强提出了一个改进的相位调制方法模拟畸形波。调制部分组成波的随机初相位，使该部分组成波的波高在预定地点和预定时间为正，波浪在此叠加形成畸形波。本文在此基础上，提出采用方向谱为靶谱进行相位调制，定时定点生成短峰非规则畸形波的方法，思路如下：

设在位置x=x_c、y=y_c，t=t_c时刻时生成畸形波，调制ε_ij使部分（或者全部）组成波在x=x_c，y=y_c，t=t_c时${\eta _i}({x_c},{y_c},{t_c})$为正，则在此叠加的波高会增大。令组成波数M=M₁ + M₂，则式（4）可以写为：

$\begin{array}{*{20}{l}} \begin{array}{l} \eta (x,y,t) = \sum\limits_{i = 1}^{{M_1}} {\sum\limits_{j = 1}^J {a_{ij}}\cos ({k_i}x\cos {\theta _j} + {k_i}y\sin {\theta _j} - {\omega _i}t + {\varepsilon _{ij}})} + \\ \;\;\;\;\;\;\;\sum\limits_{i = {M_1} + 1}^M \sum\limits_{j = 1}^J {{a_{ij}}\cos ({k_i}x\cos {\theta _j} + {k_i}y\sin {\theta _j} - {\omega _i}t + {\varepsilon _{ij}}),} \end{array} \end{array}$

(9)

$\begin{array}{l} {\eta _1}(x,y,t) = \sum\limits_{i = 1}^{{M_1}} {\sum\limits_{j = 1}^J {{a_{ij}}} } \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cos ({k_i}x\cos {\theta _j} + {k_i}y\sin {\theta _j} - {\omega _i}t + {\varepsilon _{ij}}) 。 \end{array}$

(10)

$\begin{array}{l} {\eta _2}(x,y,t) = \sum\limits_{i = {M_1} + 1}^M {\sum\limits_{j = 1}^J {{a_{ij}}} } \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cos ({k_i}x\cos {\theta _j} + {k_i}y\sin {\theta _j} - {\omega _i}t + {\varepsilon _{ij}}) 。 \end{array}$

(11)

在此，令后M₂个组成波的合成波波面${\eta _2}(x,y,t)$在预定位置处聚焦出现大波，需要调制后M₂个组成波的初相位θ_i，使${\eta _i}({x_c},{y_c},t)$。

1）当${k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c} < 0$时，令整数$N = {\rm{int}}\left[{\left( {{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c}} \right)/2{\rm{ \mathsf{ π} }}} \right]$，此时N < 0，式（7）可以写为：

$\begin{array}{l} {\eta _2}({x_c},{y_c},{t_c}) = \sum\limits_{i = {M_1} + 1}^M \sum\limits_{j = 1}^J {{a_{ij}}\cos \left( {{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j})} \right.} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\omega _i}{t_c} - 2N{\rm{\pi }} + {\varepsilon _{ij}}} \right) 。 \end{array}$

(12)

调制θ_i，使$- {\rm{ \mathsf{ π} }}/2 < {k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c} - 2N{\rm{ \mathsf{ π} }} + {\varepsilon _{ij}} < {\rm{ \mathsf{ π} }}/2$，这样$\cos \left( {{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c} - } \right.\left. {2N\pi + {\varepsilon _{ij}}} \right) > 0$，此时${\eta _i}({x_c},{y_c},{t_c}) > 0$，${\eta _2}({x_c},{y_c},{t_c}) > 0$，由于$- 2{\rm{ \mathsf{ π} < }}{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c} - 2N{\rm{ \mathsf{ π} < }}0$，θ_i在下述区间随机取值：

${\theta _i} \in \left\{ \begin{array}{l} \begin{array}{*{20}{l}} \begin{array}{l} \left( {0,{\rm{ \mathsf{ π} /}}2} \right),- {\rm{ \mathsf{ π} /}}2 < {k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\omega _i}{t_c} - 2N{\rm{ \mathsf{ π} < }}0 \end{array} \end{array}\\ \left( {{\rm{ \mathsf{ π} }}/2,{\rm{ \mathsf{ π} }}} \right),- {\rm{ \mathsf{ π} < }}{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\omega _i}{t_c} - 2N{\rm{ \mathsf{ π} < }} - {\rm{ \mathsf{ π} }}/2\\ \left( {{\rm{ \mathsf{ π} ,3}} \times {\rm{ \mathsf{ π} /}}2} \right),- 3{\rm{ \mathsf{ π} /2 < }}{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\omega _i}{t_c} - 2N{\rm{ \mathsf{ π} < }} - {\rm{ \mathsf{ π} }}\\ \left( {{\rm{3}} \times {\rm{ \mathsf{ π} /}}2,2 \times {\rm{ \mathsf{ π} }}} \right),- 2{\rm{ \mathsf{ π} < }}{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\omega _i}{t_c} - 2N{\rm{ \mathsf{ π} < }} - 3{\rm{ \mathsf{ π} /2}} 。 \end{array} \right.$

(13)

2）当${k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c} \ge 0$时，令整数$N = {\rm{int}}\left[{\left( {{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c}} \right)/2{\rm{ \mathsf{ π} }}} \right]$，此时N≥0，式4可以写为

$\begin{array}{l} {\eta _2}({x_c},{y_c},{t_c}) = \sum\limits_{i = {M_1} + 1}^M \sum\limits_{j = 1}^J {{a_{ij}}\cos \left( {{k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j})} \right.} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\omega _i}{t_c} - 2(N + 1){\rm{ \mathsf{ π} }} + {\varepsilon _{ij}}} \right) 。 \end{array}$

(14)

调制θ_i, 使$- {\rm{ \mathsf{ π} }}/2 < {k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c} - 2(N + 1){\rm{ \mathsf{ π} }} + {\varepsilon _{ij}}$，$< {\rm{ \mathsf{ π} }}/2$这样${k_i}({x_c}\cos {\theta _j} + {y_c}\sin {\theta _j}) - {\omega _i}{t_c} - 2(N + 1){\rm{ \mathsf{ π} }} + {\varepsilon _{ij}} > 0$，此时${\eta _i}({x_c},{y_c},{t_c}) > 0$，${\eta _2}({x_c},{y_c},{t_c}) > 0$，θ_i的确定方法与情况（1）中所述相同，不再赘述。

3 数值模拟及验证 3.1 数值模拟方案

靶谱采用Jonswap谱，有义波高H_1/3=0.1 m，谱峰升高因子γ=3.3，谱峰周期T_p=1.2 s，频率范围为$f = 0.5{f_p}2.5{f_p}$；子波个数为30，即M=30，既能满足生成畸形波的需求又尽可能地减少了计算量，采用高频向低频的调制方式。方向扩散个数为13，区间（-π/2，π/2），等间距分布，其中主波向180°；假设生成畸形波的预定位置和预定时间分别设为x_c=4 m、y_c=0 m和t_c=10 s，在（x=4 m，y=0 m）设置浪高仪进行时历监测。

虽然研究者对畸形波的定义存在分歧，但都不否认畸形波的波高大于2.0倍的有效波高。

本文采用H_max/H_1/3≥2.0作为畸形波定义的主要条件。

3.2 数值模拟结果

在Matlab语言环境下，根据以上数学模型进行数值模拟，得到t_c=10 s时刻瞬时波面如图 4所示。

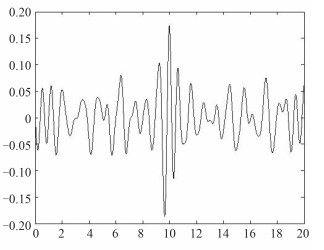
从图 4可看出，该实验成功模拟出短峰非规则波，并在预定位置生成了畸形波，图 5显示预定位置处在10 s时刻，波高为0.37，超过有义波高的2倍，说明出现了畸形波，达到了预期目标。

3.3 结果验证

为了进行验证，实验过程中还在以（6，0）为圆心，以0.5倍的谱峰波长（L=1.1）为半径的圆上顺时针每隔72°布设5个浪高仪^[9]。如图 6所示

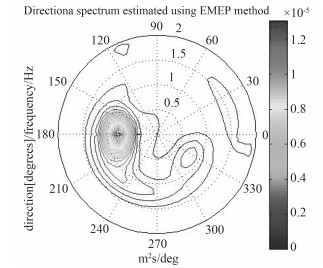
采用拓展的最大熵法（EMEP）对波高时历进行谱分析^[10]，得到模拟方向谱如图 7所示。将得到的模拟方向谱各参数与目标谱对比如表 1所示。

从谱分析得到的结果来看，数值模拟的有义波高与目标值相对误差是7.8%，谱峰周期相对误差4.2%，主浪向相对误差-0.5%，模拟效果较好。

4 结语

总体来看，本研究提出的在Matlab语言环境下生成短峰非规则畸形波的数值模拟方案，实现了在预定时间和位置生成畸形波的目的，且精度较高，为以后进行畸形波的CFD数值造波技术等研究提供了新思路。研究提出的相位调制方案，是在前人的基础上进行修改，各参数的优化选择如方向扩散个数、组成波个数等还需要后续实验探索。