2. 江苏科技大学 能源与动力工程学院,江苏 镇江 212003
2. School of Energy and Power Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China
随着综合国力增强,我国越来越重视对海洋的开发。据资料显示,世界海底石油可采储量约占总可采储量的45%,海底天然气的储量约占总储量的50%~55%;在海底还蕴藏着如煤矿、铁矿、热液矿藏、可燃冰等丰富的矿产资源。在我国东海和南海发现了可燃冰,据测算仅我国南海的可燃冰资源就达700 t油当量,相当于中国陆上油气资源量总数的1/2[1]。在众多的海上工程实施中,运输起吊工作成了一个极具挑战性的问题。主要是由于海面天气情况比较复杂,海面上浮式起重机的吊钩进行起吊重物,时常会受到波浪的作用而产生晃动,当吊钩的晃动超过一定的范围就会造成施工事故[2-3]。为了提高施工效率,有效克服海上浮式起重机在作业时所受波浪影响,荷兰barge master公司设计了1套三自由度波浪补偿控制平台。本文以此为研究对象,对其主要的液压元件添加传递函数,建立液压系统模型,在控制系统中应用PD控制算法。传递表明此方法能使系统实现所需精度及稳定性要求。
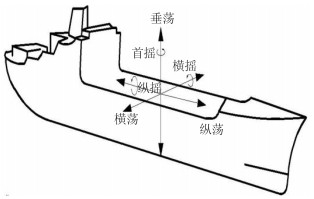
1 电液伺服控制系统船舶在海面上航行所受的波浪一般可分为6个自由度。如图 1所示,分别为横摇、纵摇、首摇、横荡、纵荡、垂荡。其中的横荡、纵荡与首摇可以借助船舶动力定位系统或者锚泊技术来实现控制补偿,但是对于横摇、纵摇以及垂荡依靠船舶自身很难实现有效补偿,并且起吊机在作业过程中许多的施工事故都是由于这3种自由度运动所造成,鉴于此所设计的波浪补偿控制平台(见图 2),主要是为了实现对横摇、纵摇以及垂荡的补偿。
|
图 1 船舶6个自由度运动 Fig. 1 The ship's motion of six freedom degree |

|
图 2 三自由度波浪补偿控制平台结构 Fig. 2 The structure of three degree freedom wave compensation platform |
在实际操作过程中,由于浮式起重机起吊重物时易受风浪作用会产生较大的扭矩,因此不能采用电机驱动而选择液压驱动。此外,在液压缸上升及下降过程中,会经常出现振动、噪声、冲击、爬行等异常工作状态,这主要是由于液压传动介质具有流动性、压缩性、粘度等特性所造成[4],因此对液压缸的控制尤为需要。电液伺服系统结合电气和液压技术特点,可以实现对液压缸运动精确控制,因此对电液伺服控制系统的研究至关重要。
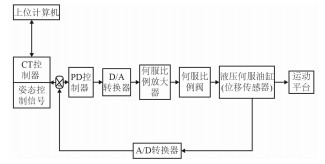
2 控制系统原理及传递函数建立 2.1 控制系统的组成与原理波浪补偿控制系统由微机控制系统及闭环液压系统组成。微机控制系统主要包括上位机、CT控制器和数据采集卡等。闭环液压系统由位置传感器、伺服比例放大器和液压伺服缸等组成。其工作原理如图 3所示,上位机通过网络通讯将期望位置姿态信号传输给CT控制器,CT控制器通过位置的转换和解算,得到3只液压伺服油缸所需的位移行程,通过数模转换装置将数字量转换到模拟器件,来控制伺服比例放大器及比例伺服阀,从而控制3只液压伺服油缸的行程,安装在液压伺服油缸上的位移传感器将位置反馈,与期望的位置进行比较,通过PD调节使误差控制在合理范围之内。
|
图 3 控制系统的组成原理 Fig. 3 The composition of control system |
电液伺服系统具有控制精度高、响应速度快、输出功率大、信号处理灵活、易于实现各种参数的反馈等优点[5]。精确数学模型的建立对于实现电液伺服系统精确控制起着决定性作用。
液压缸连续性流量方程:
| $ {Q_l} = {C_{ie}}{P_L} + {C_f}{P_s} + \left( {{V_t}/4{\beta _e}} \right){\dot P_L} + {A_p}\dot x{\text{。}} $ | (1) |
式中:Ql为负载流量,m3/s;Cie为等效泄漏系数,m5/N·s;PL为负载压力差,N/m2;Cf为附加泄漏系数,m5/N·s;Ps为液压油源的压强,Pa;Vt为液压缸等效总体积,m3;βe为系统有效弹性模量,Pa;Ap为活塞面积,m2;x为活塞杆位移,m/s;。
电液伺服阀线性化流量方程:
| $ {Q_l} = {K_q}{x_v} - {K_{ce}}{P_L}{\text{。}} $ | (2) |
式中:Kq为流量增益,m2/s;Kce为滑阀流量压力放大系数,m3/s·Pa;xv为滑块阀芯相对;Mt为活塞所承受重量,kg;Bp为活塞的阻尼系数,N/m·s-1;k为负载弹簧刚度,m/s;FL为施加在活塞杆上的外力,N。
伺服控制系统主要以惯性负载为主,一般可以忽略弹性负载。因此对式(1)~式(3)进行拉斯变化,得到液压缸传递函数:
| $ Y\left( S \right) = \frac{{\frac{{{K_q}}}{{{A_q}}}{x_v} - \frac{{{K_{ce}}}}{{{A^2}_p}}\left( {1 + \frac{{{V_t}}}{{4{\beta _e}{K_{ce}}}}} \right){F_L}}}{{s\left( {\frac{{{s^2}}}{{{\omega ^2}h}} + \frac{{2{\zeta _h}}}{{{\omega _h}}} + 1} \right)}}{\text{,}} $ | (3) |
式中:ωh为液压固有频率,rad/s;ζh为液压阻尼比,量纲唯一。
| $ {\omega _h} = 2\sqrt {\frac{{{\beta _e}{A^2}_p}}{{{M_t}{V_t}}}} {\text{,}} $ | (4) |
| $ {\zeta _h} = \frac{{{K_{ce}}}}{{{A_p}}}\sqrt {\frac{{{\beta _e}{M_t}}}{{{V_t}}}} + \frac{{{B_p}}}{{4{A_p}}}\sqrt {\frac{{{V_t}}}{{{\beta _e}{M_t}}}} {\text{,}} $ | (5) |
系统液压固有频率高于50 Hz时,伺服阀的传递函数优选2介环节,其传递函数为:
| $ \frac{{{q_l}}}{{\Delta i}} = \frac{{{k_{sv}}}}{{\frac{{{s^2}}}{{{\omega _{sv}}}} + 2\frac{{{\zeta _{sv}}}}{{{\omega _{sv}}}}s + 1}}{\text{,}} $ | (6) |
式中:∆i为差动电流;ksv为伺服阀增益;ωsv为伺服阀带宽;ζsv为伺服阀阻尼系数。
伺服放大器一般优选比例环节和位移传感器传递函数为:
| $ I\left( s \right) = {K_a}{U_s}{\text{,}} $ | (7) |
式中:I为放大器输出电流,A;Ka为伺服放大器增益,A/V;U为伺服放大器输入电压,V。
位移传感器由于频宽比系统频宽高的多,因此一般采用比例环节,其传递函数为:
| $ {U_f}\left( s \right) = {x_p}{\rm{\cdot}}{K_f}{\text{。}} $ | (8) |
式中:Uf为位移反馈值,V;Kf为位移传感器增益参数,V/m。
电液伺服控制系统传递函数
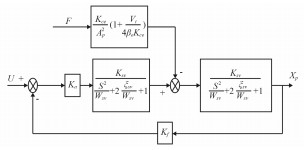
由式(4),式(7),式(8),式(9)可以确定电液伺服控制系统的传递函数框图如图 4所示。
|
图 4 控制系统方块图 Fig. 4 Control system block diagram |
AMEsim为多学科领域复杂系统建模仿真平台,用户可以在这单一平台上建立复杂的多学科领域系统模型,并在此基础上进行仿真计算和深入分析,也可以在这个平台上研究任何元件或系统的稳态和动态性能[6]。同时该软件具有强大的接口技术,可以与ADAMS、Matlab以及其他工程软件进行联合仿真,使仿真工作范围更加宽广,仿真更加方便。
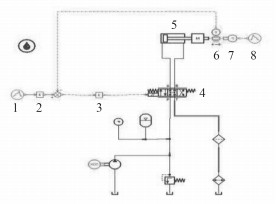
波浪补偿装置采用单通道控制策略,液压控制回路可以分为3个单通道回路,然后将3个单通道回路并联在一起,因此模型只需要建立一个单通道回路即可。图 5为液压控制原理图,主要包括电动马达、液压泵、伺服阀、信号输出器、位移传感器、力传感器及伺服阀4的液压油流量,最终实现伺服缸的运动;在经过位移传感器将伺服缸位移值进行反馈。信号输出器8模拟施加在活塞杆上的负载。
|
图 5 液压控制原理图 Fig. 5 Hydraulic control principle diagram |
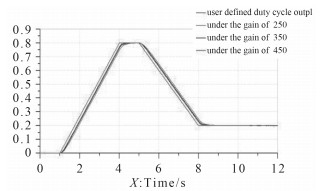
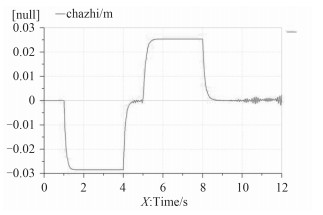
马达转速为1 500 r/min;液压泵排量为35 cc/rev,固有转速为1 000 r/min;安全阀的流量压力梯度为500 l/min,破裂压力为150 bar;伺服阀额定电流为200 mA,固有频率为50 Hz,阻尼比为1 null。液压缸活塞直径为35 mm,液压杆活塞直径为25 mm,连接质量块以及外部负载力设置为1 000 kg。考虑到电液伺服阀几乎与二阶振动元件相似,伺服放大器的增益对整个控制系统的动态性能有着很大的影响。因此,首先在其他参数不变的情况下分别对伺服放大器设置不同的增益值[7],分别为250,350,450。观察在不同增益参数时,系统的输出曲线与跟随曲线之间的误差。图 6~图 9分别为AMEsim环境下,仿真时间为12 s,时间间隔为0.05 s时的仿真曲线。
|
图 6 不同增益参数的位移输出曲线 Fig. 6 Displacement output curve under different different gain parameters |

|
图 7 增益参数250的动态误差 Fig. 7 Dynamic error of gain parameter 250 |

|
图 8 增益参数350的动态误差 Fig. 8 Dynamic error of gain parameter 350 |
|
图 9 增益参数450的动态误差 Fig. 9 Dynamic error of gain parameter 450 |
从图 6~图 9的仿真结果可知,输出信号与液压缸的响应存在一定位置误差,这是所有的液压控制系统无法避免的,主要由于实际过程中必须将误差控制在满足要求的范围之内,本装置要求必须将误差控制在30 mm以内。从图 7~图 8发现,当增益因子从250增加到350时,系统的最大动态位置误差从0.054 m减少到0.038 m。这表明通过增加开环增益可以有效减少系统动态位置误差,当开环增益从350增加到450时,系统的动态误差减少到0.028 6 m,但控制系统变得不稳定,因此对于仅仅通过增加开环增益并不能获得理想结果。从仿真结果中得知系统的动态位置误差与伺服放大器的开环增益成反比。
4 液压系统建模优化从以上仿真研究可知,仅通过改变增益参数并不能取得理想的精度及稳定性要求。在AMESim软件中拥有特殊的PD控制模块,其主要基于NLPQL和遗传算法2种优化方法。NLPQL主要思想是假设目标函数连续并且可微,将目标函数转化成二阶拉斯方程,将迭代点X(k)作为二次规划子问题[8],根据迭代公式
基于以上2种优化方法,在AMESIM仿真平台上选择遗传算法对PD控制器的2个参数进行优化。首先确认参数范围,应用AMESIM批量处理功能对电液伺服位置系统PD控制器的Kp和Kd参数批量处理,观察对输出响应的活塞杆位移参数变化的影响,排除对动态跟踪误差参数太大的和稳定性差的参数。批处理参数范围如下:
Kp取值范围:100,200,300,400,500,600,700,800;
Kd取值范围:0.01,0.05,0.1,1,5,50,100,200。
然后选择AMESIM中的design和development模块,采用遗传算法进行优化。为了避免选择参数过大,先将一部分参数处理得到大致的参数范围,然后再采用遗传算法进行优化设计,从而可以减少初始优化的盲目性,节省计算量。在AMESIM中设置算法参数,种群规模40,复制概率为0.7,变异概率为0.1,变异幅值为0.6,遗传迭代数为50,超过接近4 000次迭代运算。得出最优的Kp和Kd参数为:Kp=525.21,Kd=0.04。
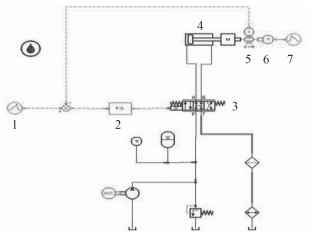
按照图 10的优化模型定义Kp=525.21,Kd=0.04,其他元件参数与图 5的参数设置一样,设置系统的仿真时间为12 s,时间间隔为0.05 s,图 11为仿真分析结果。
|
图 10 优化后的液压控制原理图 Fig. 10 After optimization of the hydraulic |
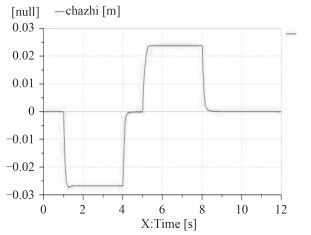
|
图 11 在PD控制器下的动态误差 Fig. 11 Dynamic error in PD controller control principle diagram |
对比优化前与优化后的仿真曲线得知,通过增加PD控制器,系统的精度及稳定性有了很大的改进,系统的动态位置误差减少到0.027 3 m,该误差比在不采用PD控制算法精度提高了40%,且系统具有一定的稳定性。因此采用PD控制算法控制调节,系统具有良好的跟随特性,可以实现本装置的精度及稳定性要求。
5 结语本文利用AMESIM建立波浪补偿控制平台液压图,分析不同开环增益下的系统动态性能,并提出了使用PD控制算法对液压控制系统进行优化,来满足系统精度要求。
1)从图 6~图 9可知,可以通过增加伺服系统增益参数,来减少液压系统的动态位置误差,但随着伺服增益参数的增加,系统输出曲线开始不稳定,发生扰动,因此增加伺服增益参数在一定程度上可以实现提高精度。
2)基于遗传算法进行PD参数的优化选择,可以进行多个参数共同比较,过程简单,同时具有很好的收敛性,避免了盲目筛选参数从而提高工作效率。
3)经过图 10~图 11的仿真研究,说明PD控制算法不但简单而且能够保证系统具有一定的精度及稳定性,能够使一个低稳定性的液压系统变为高稳定性,并且更好地跟随参考模型输出希望数值曲线。
| [1] |
郑苗壮, 刘岩, 李明杰, 等. 我国海洋资源开发利用现状及发展趋势[J]. 海洋开发与管理 , 2013 (12) :13–16.
ZHENG Miao-zhuang, LIU Yan, LI Ming-jie, et al. Current situation and trend of the development and utilization of marine resources in China[J]. Ocean Development and Management , 2013 (12) :13–16. |
| [2] |
王孝霖, 顾含, 许历, 等. 波浪补偿起重机液压系统设计与分析[J]. 船舶标准化工程师 , 2015 (4) :63–66.
WANG Xiao-lin, GU Han, XU Li, et al. Design and analysis of hydraulic system of wave compensation crane[J]. Ship Standardization Engineer , 2015 (4) :63–66. |
| [3] |
王颖, 韩光, 张英香. 深海海洋工程装备技术发展现状及趋势[J]. 舰船科学技术 , 2010, 32 (10) :108–113, 124.
WANG Ying, HAN Guang, ZHANG Ying-xiang. The development of deep water ocean engineering equipments and technology[J]. Ship Science and Technology , 2010, 32 (10) :108–113, 124. |
| [4] |
王龙, 徐永宏, 周庆年. 液压爬行现象及其控制[J]. 液压气动与密封 , 2010 (11) :6–8.
WANG Long, XU Yong-hong, ZHOU Qing-nian. The creeping phenomenon of hydraulic and the method to control[J]. Hydraulics Pneumatics & Seals , 2010 (11) :6–8. |
| [5] | YANADA H, FURUTA K. Adaptive control of an electrohydraulic servo system utilizing online estimate of its natural frequency[J]. Mechatronics , 2007, 17 (6) :337–343. DOI:10.1016/j.mechatronics.2007.04.007 |
| [6] |
梁全, 苏齐莹.
液压系统AMESim计算机仿真指南[M]. 北京: 机械工业出版社, 2014 : 173 -200.
LIANG Quan, SU Qi-ying. Guide for computer simulation of hydraulic system AMESim[M]. Beijing: China Machine Press, 2014 : 173 -200. |
| [7] |
黄元峰, 刘源, 谈宏华. 电液伺服系统的增益自适应滑模变结构控制[J]. 大连海事大学学报 , 2008, 34 (2) :73–78.
HUANG Yuan-feng, LIU Yuan, TAN Hong-hua. Gain adaptive sliding mode variable structure control in electro-hydraulic servo system[J]. Journal of Dalian Maritime University , 2008, 34 (2) :73–78. |
| [8] |
杨永锋, 任兴民, 秦卫阳, 等. 基于层次分析法的MDO算法性能评价[J]. 机械科学与技术 , 2007, 26 (1) :108–111.
Yang Yong-feng, Ren Xing-min, Qin Wei-yang, et al. MDO algorithm performance evaluation based on analytic hierarchy process[J]. Mechanical Science and Technology , 2007, 26 (1) :108–111. |
| [9] |
边霞, 米良. 遗传算法理论及其应用研究进展[J]. 计算机应用研究 , 2010, 27 (7) :2425–2429, 2434.
BIAN Xia, MI Liang. Development on genetic algorithm theory and its applications[J]. Application Research of Computers , 2010, 27 (7) :2425–2429, 2434. |
 2016, Vol. 38
2016, Vol. 38
