近年来,软刚臂单点系泊系统作为近海定位的重要系泊方式受到越来越多的关注,为了准确预报系泊系统在风浪流联合作用下的受力情况,国内外学者做了很多的研究。范模[1]推导出了系泊系统纵向刚度曲线计算公式,与国外公司和模型试验的结果非常吻合;李欣[2]采用多体方法,建立了软刚臂系统纵荡/垂荡方向的振动方程,通过导入试验的实测数据,反推验证了单点模型的合理性;孙晔[3]提出了通过测量角度变化,计算系泊力的方案,较好地解决FPSO系泊力测量的难题;李淑一[4]基于多体动力分析方法研究了FPSO和水下软钢臂系泊系统的运动特性,分析了水下A字型钢臂的黏性力和二阶波浪力对系统响应的影响;陈光[5]通过对FPSO软刚臂单点系泊系统的现场监测,研究了引起共振产生的原因;夏华波[6]从实用性和经济性方面考虑,提出了一种可调节系泊臂铰接点高度的系泊方案。
水上软钢臂单点系泊系统在实际海况作用下的受力情况对于系泊系统的设计非常的重要,若实际受力超过设计值,可能会发生系泊系统和船舶相撞的情况,甚至可能出现由于系统强度不够破坏整个系泊结构,造成难以弥补的后果。
本文以渤海海域某水上软钢臂单点系泊系统的方案设计为计算模型,运用多体水动力学软件AQWA,对该系泊系统进行频域水动力分析和时域运动响应分析,得到在不同风浪流方向组合下的关键结构受力仿真结果,讨论风浪流夹角对系泊系统受力的影响。
1 计算方法和理论 1.1 计算流程本文采用多体水动力学软件AQWA建立船舶和系泊系统的仿真分析模型,并进行水动力分析。包括用于频域计算的AQWA-LINE模块和用于时域计算的AQWA-DRIFT模块。
AQWA-LINE模块用于计算在船体周围由于波浪辐射和衍射作用而产生的波浪力,同时也可以求解出船舶的附加质量和附加阻尼。
AQWA-DRIFT模块通过调用AQWA-LINE结果文件中的幅值响应算子、附加质量、辐射阻尼等数据,计算在给定的随机风浪流条件下系泊系统以及船舶之间的受力随时间变化的情况。最后利用AQWA的后处理模块AGS读取分析结果。
1.2 理论基础AQWA基于三维势流理论,不考虑粘性,假设为不可压缩的理想流体,因此整个流体可以用势函数来表示。并且速度势满足拉普拉斯方程,解出速度势
| ${\nabla ^2}\phi = 0(\mathit{\boldsymbol{V}} = \nabla \phi ),$ | (1) |
再由拉格朗日方程得到船体表面的压力分布:
| $\frac{{\partial \varphi }}{{\partial t}} + \frac{p}{\rho } + \frac{1}{2}{v^2} + gz = f\left( t \right),$ | (2) |
一阶波浪力的速度势为:
| $\phi = \varphi {e^{ - i\omega t}} = \left[{\left( {{\varphi _i} + {\varphi _d}} \right) + \sum\limits_{j = 1}^6 {{\varphi _j}} {x_j}} \right]{e^{ - i\omega t}},$ | (3) |
式中:ω为规则波浪的圆频率;φi为入射波速度势;φd为绕射波速度势;φj为各自由度方向的速度势。
解出1阶波浪力速度势后,由伯努利方程求解表面水压力:
| $P = - \rho \frac{{\partial \varphi }}{{\partial t}},$ | (4) |
再对船体的湿表面进行积分即可得到1阶波浪力:
| ${F_j} = - \int {^P} {n_j}{\rm{d}}s,$ | (5) |
式中:Fj为船体在第j个自由度上的1阶波浪力;nj为第j个自由度的法向。
频域计算时,船舶在波浪中的受力主要由入射力和绕射力两部分,并且认为他们都是简谐的。
再通过以下运动方程,求解出船舶在单位波幅的规则波浪下的幅值响应算子,即RAO。
| $\mathit{\boldsymbol{M}}s\left( \omega \right)\dot X + \mathit{\boldsymbol{M}}\alpha \left( \omega \right)\dot X + C\left( \omega \right)\dot X + \mathit{\boldsymbol{K}}s\left( \omega \right)X = F\left( \omega \right),$ | (6) |
式中:Ms为结构质量矩阵;Mα为水动力附加质量矩阵,C为系统线性阻尼矩阵;Ks为系统总刚度矩阵;F为系统所受的波浪力(单位波高);X为幅值响应算子(RAO);ω为入射规则波频率。
时域计算时,利用波浪谱来实现随机波浪载荷的动力效应,本文选取JONSWAP谱来模拟。
| $\begin{array}{*{20}{l}} \begin{array}{l} S\left( f \right) = {\beta _J}H_{1/3}^2T_p^{ - 4}{f^{ - 5}},\\ {\rm{exp}}\left[{ - 1.25{{({T_p}f)}^{ - 4}}} \right]{\gamma ^{exp[- \left( {{T_p}f - 1{)^2}/2{\sigma ^2}} \right)}} 。 \end{array} \end{array}$ | (7) |
式中:βJ为能量尺度参量;H1/3为有义波高;TP为谱峰周期;γ为峰值增长因子;σ为波峰因子。
根据选定的JONSWAP谱,通过傅里叶变换可以得到时域内的随机波面升高,进而通过卷积积分的方式的得到波浪载荷的时域历程,进而得到系泊系统结构受力的时域历程曲线。
2 单点系泊系统模型 2.1 船舶有限元模型表 1给出了船舶的主尺度参数。由船舶的型值表建立模型,依据吃水切分水线并划分面元网格,如图 1所示,共划分节点4 129个,单元4 039个,能满足计算最大波浪频率为2.345 rad/s的海况。
|
|
表 1 船舶主要特征参数 Tab.1 Main characteristic parameters of the ship |

|
图 1 单点系泊系统的水动力模型 Fig. 1 Hydrodynamic model of the tower soft yoke single mooring system |
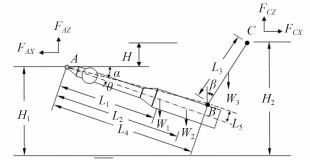
本文船舶采用的是一种水上塔架软钢臂系泊系统,该系泊系统主要由系泊塔架、软钢臂(即YOKE)、系泊腿(即LEG)和船舶支撑结构(即MSS)组成。
|
图 2 系泊系统计算模型图 Fig. 2 Calculation model plan of the mooring system |
|
|
表 2 系泊机构主要特征参数 Tab.2 Main characteristic parameters of the mooring system |
系泊系统内部的连接方式设置如下:
1)软钢臂前端点和系泊塔架依靠扼头和转盘连接,使之能够绕系泊塔架单点处自由转动,所以在AQWA中将它们之间的连接方式简化为球铰;
2)软钢臂和左右系泊腿之间以及左右系泊腿和船舶支撑结构之间通过万向铰连接,释放3个方向的转动自由度,所以在AQWA中将万向铰的连接方式简化为球铰;
3)船舶支撑结构和船体之间采用刚性固定。
2.3 环境载荷为了模拟仿真不同风浪流夹角对软钢臂系泊系统受力的影响,本文依据渤海海洋环境确定了6组计算工况如表 3所示。
|
|
表 3 不同工况下的环境载荷 Tab.3 Possible ocean environment loads |
由于AQWA-DRIFT模块进行的时域耦合分析是建立在基于三维势流理论对船舶进行辐射绕射分析的基础上的,所以要首先运用AQWA-LINE模块求解不同波浪角不同波浪频率下的规则波下的船舶的幅值响应算子、附加质量及辐射阻尼等。
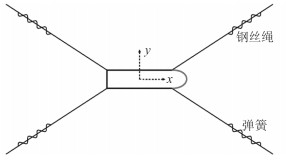
进行水动力分析时采用势流理论并没有考虑水的粘性作用引起的阻尼,所以根据图 3所示进行静水自由衰减试验,测出阻尼比,再由阻尼比进行估算实船的粘性阻尼系数,如表 4所示。
|
图 3 静水自由衰减实验示意图 Fig. 3 Test methods for damping of the ship |
|
|
表 4 实船的粘性阻尼系数 Tab.4 Damping coefficient of the ship |
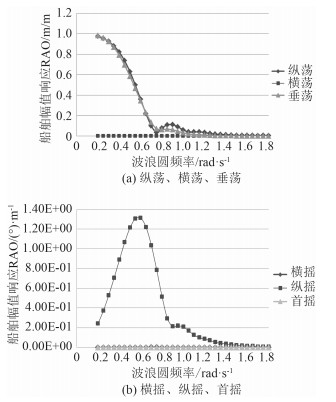
软钢臂系泊系统在实际使用过程中,由于风向标效应,船舶一般处于迎浪状态,故本节只选取频域计算结果中浪向角为180°的情况,船舶在6个自由度方向上的幅值响应算子RAO如图 4所示。由图可知,在180°浪向角方向下,横荡、横摇和首摇方向的RAO值接近于0,这与实际情况相符合;当波浪频率大于1.5 rad/s,其余3个方向的RAO值也趋近0;当波浪频率小于0.8 rad/s时,纵荡、垂荡、横摇比较明显。
|
图 4 船舶幅值响应RAO曲线 Fig. 4 Response amplitude operator of the ship |
可见,软钢臂系泊系统在波浪低频作用下远比波浪高频作用下更危险,在进行软钢臂设计和校核的过程中必须确保系泊系统的固有频率和波浪频率不发生共振;而且,当对船舶稳性、耐波性要求比较高时,可以考虑为船舶安装减摇装置。
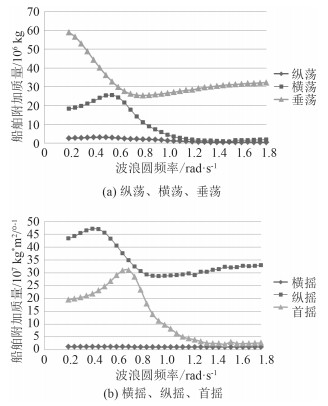
3.2 船舶附加质量船舶在6个自由度下的附加质量如图 5所示,横摇、首摇、垂荡方向的附加质量比较大,且在当波浪频率大于0.7时,横荡、纵荡、横摇、首摇方向的附加质量随着波浪频率的增大而减小。
|
图 5 船舶附加质量曲线 Fig. 5 Additional mass and additional inertia of the ship |
船舶在6个自由度下的辐射阻尼见图 6,对比计算所得的辐射阻尼和表 4模型实验出的水阻尼可以发现,静水自由衰减实验测出的垂荡、横摇、纵摇方向水阻尼比辐射阻尼大很多,因此,进行水动力计算前通过静水模型实验准确的测量出水阻尼十分重要。
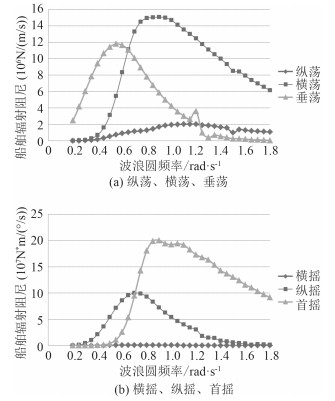
|
图 6 辐射阻尼曲线 Fig. 6 Radiation damping of the ship |
通过AQWA-DRIFT模块调用AQWA-LINE的计算结果,并进行时域响应分析,分析时长3 h,步长0.2 s,得到船舶在如表 3所示的6种工况下的运动响应和主要结构的受力情况。
为了确保系泊系统运行的安全,主要内容有:
1)确保船舶和系泊系统不发生碰撞或者极限拉伸的情况;
2)确保系泊系统在运动中所受载荷满足强度和疲劳校核。
系泊系统单点处的水平力、垂向力和系泊腿的轴向力是其校核依据。
在AGS模块中调用AQWA-DRIFT分析的结果文件,模拟船舶的实时运动,发现并未产生碰撞或者极限拉伸的现象,且转塔处风向标效应良好。
系泊系统单点处的水平力、垂向力和系泊腿的轴向力的时域曲线如图 7所示。系泊系统时域分析关键结构所受载荷幅值情况统计如表 5所示。
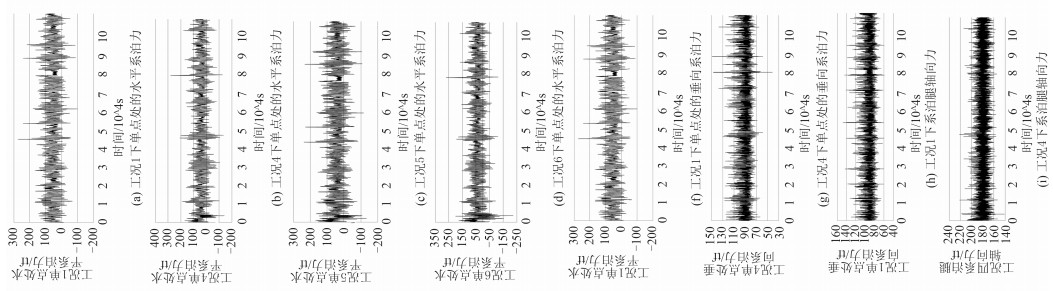
|
图 7 不同海洋环境条件下的系泊系统应力曲线 Fig. 7 Stress of the mooring system due to diffent ocean environment conditions |
|
|
表 5 系泊系统受力幅值情况,tf Tab.5 Amplitude of the structure force, tf |
计算结果表明:
1)在未发生极限拉伸或者碰撞的情况下,风浪流的方向夹角对系泊系统单点处的水平力影响很大,且最大受力值并非发生在180°风浪流同向的情况下,系泊系统单点水平受力情况大到小排序如下:工况2>工况4>工况1>工况5>工况6>工况3。
2)在未发生极限拉伸或者碰撞的情况下,风浪流的方向夹角对系泊系统单点处的垂向力和系泊腿轴向力影响很小,变化量均在10%以内。
3)在未发生极限拉伸或者碰撞的情况下,系泊系统单点处的水平力幅值和垂向力幅值的变化呈现正相关趋势,并且从6种工况的时域曲线图上可以发现,水平系泊力出现极大值的时刻和垂向系泊力出现极大值的时刻也相近。
4)工况5和工况6下的分析时域曲线图上可以发现,系泊系统单点处的水平力在刚开始的时候出现较大波动,主要原因是此时的系泊力无法和风浪流合力进行平衡,在风向标效应的作用下,船舶和系泊结构绕塔架发生旋转,使得单点处Y方向水平力出现较大波动,直至船舶处于一个相对平衡的状态后,此波动消失。
5 结语本文先通过频率分析,发现软钢臂系泊系统在波浪低频作用下比高频作用下更危险;对比静水阻尼和辐射阻尼,发现水阻尼的数值大于辐射阻尼,在水动力分析时不能忽略。
通过对水上软钢臂单点系泊系统在不同风浪流夹角下的受力分析,认为在各种工况下,风向标效应较为明显,其中在工况2下,即风浪同向180°,流向135°组合下,单点处水平载荷最大,确定其为最危险工况,后续关于系泊结构、塔架以及连接处万向节的强度和疲劳校核应该满足此工况。
| [1] |
范模. 软刚臂单点系泊系统分析[J]. 中国海上油气(工程) , 1992, 4 (1) :29–33.
FAN Mo. The analysis for soft yoke single point mooring system[J]. China Offshore oil and Gas (Engineering) , 1992, 4 (1) :29–33. |
| [2] |
李欣, 杨建民, 肖龙飞. FPSO软刚臂单点系泊系统动力分析[J]. 中国造船 , 2005, 46 (S1) :141–148.
LI Xin, YANG Jian-min, XIAO Long-fei. Dynamic analysis on the tower-yoke mooring system of FPSO[J]. Shipbuilding of China , 2005, 46 (S1) :141–148. |
| [3] |
李欣, 杨建民, 肖龙飞. FPSO软刚臂单点系泊系统动力分析[J]. 中国造船 , 2005, 46 (S1) :141–148.
LI Xin, YANG Jian-min, XIAO Long-fei. Dynamic analysis on the tower-yoke mooring system of FPSO[J]. Shipbuilding of China , 2005, 46 (S1) :141–148. |
| [4] |
李淑一, 王树青. 基于多体分析的浅水FPSO和水下软钢臂系泊系统运动特性研究[J]. 中国海洋大学学报 , 2011, 41 (9) :95–102.
LI Shu-yi, WANG Shu-qing. Coupled dynamic analysis of FPSO and underwater soft yoke SPM based on multi-body simulation method[J]. Periodical of Ocean University of China , 2011, 41 (9) :95–102. |
| [5] |
陈光. FPSO软刚臂系泊系统运动分析及减振研究[D]. 大连: 大连理工大学, 2012.
CHEN Guang. Research on motion analysis and reduction of vibration of FPSO with soft yoke SPM system[D]. Dalian: Dalian University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012394708.htm |
| [6] |
陈光. FPSO软刚臂系泊系统运动分析及减振研究[D]. 大连: 大连理工大学, 2012.
CHEN Guang. Research on motion analysis and reduction of vibration of FPSO with soft yoke SPM system[D]. Dalian: Dalian University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012394708.htm |
 2016, Vol. 38
2016, Vol. 38
