2. 船舶振动噪声重点实验室, 湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
目前,弹性板-圆柱壳结构在船舶与海洋工程领域应用十分广泛,特别在军事应用上,对弹性板-圆柱壳结构的振动和水下辐射噪声的要求越来越高。良好的振动和辐射噪声性能不仅能够延长设备的使用寿命,更重要的是能够减小被敌方的发现距离,提高我方声呐的探测能力。罗斌采用能量法研究了肋骨断面形式对圆柱壳声辐射性能的影响;吴文伟采用傅里叶变化技术研究了各结构参数对加强筋板辐射声压的影响;谢官模研究了环肋柱壳在流场中的声辐射性能;王路才研究了加肋有限圆柱壳体的边界条件对其振动和声辐射的影响。但弹性板结构对圆柱壳振动和声辐射影响的研究还不多见。本文采用三维声弹性理论研究弹性板对圆柱壳振动和水下声辐射的影响。
1 模型简介采用Abaqus软件建立弹性板-圆柱壳左舷一半干模型如图 1所示。采用笛卡尔坐标系,X轴沿圆柱壳轴向,Y轴指向左舷。圆柱壳和弹性板采用shell单元模拟,环肋和加强筋采用beam单元模拟。环肋沿圆柱壳周向均匀布置,圆柱壳两端采用带有加强筋的板封闭,弹性板布置在圆柱壳内部水平中性面位置,与圆柱壳左右舷及封板相连,弹性板上等间距布置横向和纵向加强筋, 模型参数如表 1所示。在两侧封板处分别向外延伸一个肋位,并添加简支约束,以模拟其他舱段的影响。

|
图 1 弹性板-圆柱壳模型 Fig. 1 Elastic plate-cylindrical shell model |
|
|
表 1 模型参数 Tab.1 Parameters of model |
由模态叠加法,弹性板-圆柱壳结构离散系统的节点位移可表示为:
| $\left\{ U\left( t \right) \right\}=\left[ D \right]\left\{ q\left( t \right) \right\}=\sum\limits_{r=1}^{m}{\left\{ {{D}_{r}} \right\}{{q}_{r}}\left( t \right)}\text{,}$ | (1) |
式中,Dr为第r阶模态对应的振型位移列向量;{q(t)}、qr(t)分别为广义主坐标列向量及第r阶干模态的主坐标分量。
弹性板-圆柱壳结构离散系统的主坐标公式为:
| $ {\boldsymbol a} \!\left\{ \ddot{q}\left( t \right) \right\}\!\!+\!\! {\boldsymbol b} \left\{ \dot{q}\left( t \right) \right\}\!\!+\!\! {\boldsymbol c} \left\{ q\left( t \right) \right\}\!=\!\left\{ {{f}_{e}}\left( t \right) \right\}\!+\!\left\{ {{f}_{p}}\left( t \right) \right\}\text{。}$ | (2) |
式中:a,b, c分别为结构干模态广义质量矩阵、广义阻尼矩阵和广义刚度矩阵;{fe},{fp}分别为非声介质流场外激励力对应的广义力列向量、湿表面上声介质流场作用力对应的广义水动力列向量。
频域内的弹性板-圆柱壳声弹耦合动力学方程:
| $\begin{aligned} & \left[ { - {\omega ^2}\left( {\left[ a \right] \!+\! \left[ {\boldsymbol A} \right]} \right){\rm{ \!+\! i}}\omega \left( {\left[ b \right] \!+\! \left[ {\boldsymbol B} \right]} \right) \!+\! \left( {\left[ c \right] \!+\! \left[ {\boldsymbol C} \right]} \right)} \right]\text{,}\\ & \quad \quad \,\,\left\{ q \right\} = \left\{ {{f_e}\left( \omega \right)} \right\} + \left\{ {T\left( \omega \right)} \right\}\text{。} \end{aligned}$ | (3) |
式中:A为干模态附连水质量矩阵;B为干模态附连水阻尼矩阵;C为广义恢复力系数矩阵;T(ω)为流场中传来的入射波与刚性面反射波引起的模态广义力。
根据模态叠加原理,由式(3)求出各阶干模态主坐标响应后,代入式(1)可求得船舶结构振动响应:
| $\left\{ U \right\}\text{=}\sum\limits_{\text{r}=1}^{m}{\left\{ {{D}_{r}} \right\}}{{q}_{r}}\text{。}$ | (4) |
依据每一阶干模态振型,结合流固耦合边界条件和边界积分方程,求出对应干模态振型的湿表面源强
| ${{\phi }_{R}}\left( x,y,z \right)=\sum\limits_{r=1}^{m}{{{\phi }_{r}}\left( x,y,z \right)}{{q}_{r}}\text{。}$ | (5) |
流场中的辐射声与辐射波速度势φR对应,可得频域内的辐射波声压计算式:
| $\begin{aligned} & p\left( x,y,z \right)=-{{\rho }_{0}}\left( i\omega +\overrightarrow{W}\cdot \nabla \right){{\phi }_{R}}= \\ & \quad \quad \quad \quad \quad \!\!-{{\rho }_{0}}\left( i\omega +\overrightarrow{W}\cdot \nabla \right)\sum\limits_{r=1}^{m}{{{\phi }_{r}}\left( x,y,z \right){{q}_{r}}}\text{。}\end{aligned}$ | (6) |
式中:
为了方便表述,称X轴方向为纵向,Z轴方向为横向。由于结构对称性,只在圆柱壳水平中面内布置3个测点,如图 2所示。测点距离圆柱壳或封板的距离均为1 m。在弹性板几何中心位置添加沿Z轴负方向的单位恒值激励力。

|
图 2 测点分布 Fig. 2 Testpoints distribution |
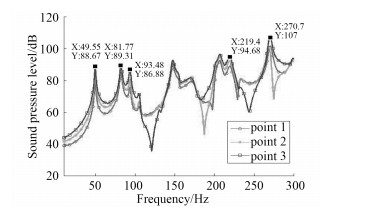
采用三维声弹性理论计算3个测点处的水下辐射声压级如图 3所示。图中标示的5个峰值点从左至右依次为弹性板1阶、2阶、3纵向模态频率点和2阶、3横向模态频率点。从图中可看到,弹性板的振动在圆柱壳水下声辐射中有明显体现,是圆柱壳水下声辐射的重要组成部分,必须引起高度重视。3个测点处的辐射声压级不同,但变化趋势基本一致。
|
图 3 测点处的辐射声压级 Fig. 3 Sound pressure level of testpoints |
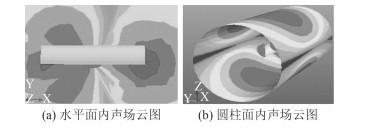
图 4为弹性板-圆柱壳水下辐射声场分布云图。从图中可看到,弹性板-圆柱壳水下辐射声场具有明显的指向性,在水平面内对称分布,且圆柱壳两端的声压级较大;圆柱面内的声场分布在圆柱壳上下两侧声压级相对较大,在左右舷相对较小,这是因为弹性板的振动主要在竖直面内,由此引起的辐射声能量也集中在竖直面内。
|
图 4 水下辐射声场云图 Fig. 4 Acoustic radiation field nephogram of underwater |
弹性板的振动模态在弹性板-圆柱壳水下声辐射中有明显体现,因此研究弹性板的结构对圆柱壳水下声辐射的影响十分必要。由于2.2节分析中,圆柱壳顶端和侧面3个测点的辐射声压级变化规律基本一致,以下分析时采用弹性板与圆柱壳连接处的振动加速度级和测点1的声压级变化作为衡量指标。
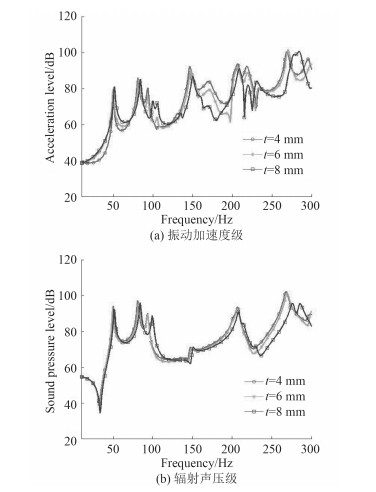
3.1 弹性板厚度的影响弹性板厚度对弹性板-圆柱壳振动和水下声辐射的影响如图 5所示。从图中可看到,随着弹性板厚度的增加,在10~300 Hz的频率区间内,测点处的振动加速度级和辐射声压级均有不同程度的下降,150 Hz频段以上下降幅度较低频段更明显。这是因为相对于低频段,高频段声辐射对结构变化更加敏感。因此在结构允许的条件下,应尽可能采用厚度大的弹性板。
|
图 5 弹性板厚度的影响 Fig. 5 Influence of elastic plate thickness |
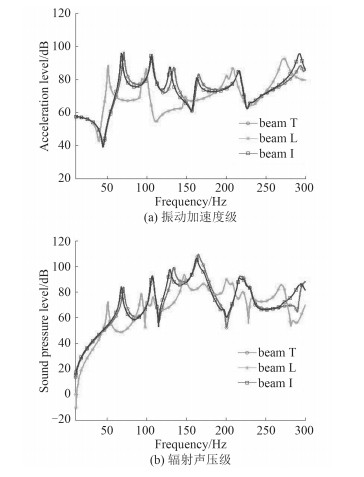
加强筋类型对弹性板-圆柱壳振动和水下声辐射的影响如图 6所示。从图中可以看到,弹性板上布置截面为T形和工字形加强筋时,测点的振动加速度级和水下辐射声压级基本一致,变化很小;布置截面为L形的加强筋时,测点处的振动加速度级和水下辐射声压级峰值频率向低频段移动,且幅值明显下降。这是因为采用不同截面类型的加强筋导致弹性板的阻抗改变,对振动的传递率改变。采用L形截面的加强筋能有效降低弹性板-圆柱壳的振动和水下辐射噪声。
|
图 6 加强筋类型的影响 Fig. 6 Influence of reinforced rib type |
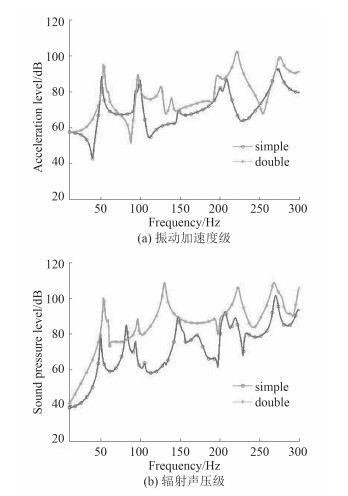
分别在圆柱壳体内水平中面位置布置单个弹性板和对称位置布置双弹性板。弹性板布置方式对弹性板-圆柱壳振动和水下声辐射的影响如图 7所示。从图中可以看到,在圆柱壳体内水平中面位置布置单个弹性板时,弹性板与圆柱壳连接处的振动加速度级明显低于在水平中面对称位置布置双弹性板;测点1处的辐射声压级曲线也表明,在圆柱壳体内水平中面位置布置单个弹性板时圆柱壳周围的辐射声压级明显比在水平中面对称位置布置双弹性板降低。因此,设计圆柱壳内部结构时,尽量采用单层弹性板形式。
|
图 7 弹性板位置的影响 Fig. 7 Influence of elastic plate location |
通过建立弹性板-圆柱壳耦合结构模型,采用三维声弹性理论计算圆柱壳体振动和水下辐射声场,得出如下结论:
1)弹性板的振动模态对圆柱壳水下声辐射有重要影响。在一定频率范围内,弹性板振动引起的圆柱壳声辐射出现较大峰值,必须予以重点关注。
2)弹性板-圆柱壳水下辐射声场呈现明显的对称性,在圆柱壳两端及上下两侧辐射声能量比较集中。
3)弹性板厚度对圆柱壳振动和声辐射有一定影响,在结构允许条件下,采用厚度较大的弹性板可以在一定程度上降低圆柱壳水下声辐射。
4)弹性板加强筋截面类型对圆柱壳振动和声辐射的影响显著,采用L形截面的加强筋可以最大程度降低圆柱壳水下声辐射。
5)在圆柱壳体内水平中面位置布置单个弹性板比对称位置布置双弹性板更能有效降低圆柱壳的振动和水下声辐射。
| [1] |
王路才, 周其斗, 纪刚. 加肋有限圆柱壳体的边界条件对其振动和声辐射的影响[J]. 船舶力学 , 2013, 17 (5) :559–566.
WANG Lu-cai, ZHOU Qi-dou, JI Gang. Effect on acoustic radiation of ribbed cylindrical shell due to boundary conditions[J]. Journal of Ship Mechanics , 2013, 17 (5) :559–566. |
| [2] |
陈清坤, 陈美霞, 和卫平, 等. 舱壁与压载对流场中有限长圆柱壳声辐射影响[J]. 舰船科学技术 , 2010, 32 (11) :21–25.
CHEN Qing-kun, CHEN Mei-xia, HE Wei-ping, et al. Impact of bulkhead and ballast on acoustic radiation of submerged finite cylindrical shell[J]. Ship Science and Technology , 2010, 32 (11) :21–25. |
| [3] | 夏齐强, 陈志坚. 舱壁振动对环肋圆柱壳舱段振声性能的影响[J]. 海军工程大学学报 , 2014, 26 (1) :23–28. |
| [4] | 周奇郑, 王德石, 高晟耀. 多源激励下水中有限长加肋圆柱壳体声振特性研究[J]. 应用力学学报 , 2013, 30 (5) :652–657. |
| [5] | LIAO C J, JIANG W K, DUAN H, et al. Vibration and sound radiation from submerged finite cylindrical shells reinforced with axially periodic stiffeners[J]. Journal of Vibration and Control , 2010, 17 (10) :1472–1480. |
| [6] | CARESTA M, KESSISSOGLOU N J. Structural and acoustic responses of a fluid-loaded cylindrical hull with structural discontinuities[J]. Applied Acoustics , 2009, 70 (7) :954–963. DOI:10.1016/j.apacoust.2008.11.004 |
| [7] | ZHOU Q, JOSEPH P F. A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J]. Journal of Sound and Vibration , 2005, 283 (3/5) :853–873. |
| [8] | 谢官模, 李军向, 罗斌, 等. 环肋、舱壁和纵骨加强的无限长圆柱壳在水下的声辐射特性[J]. 船舶力学 , 2004, 8 (2) :101–108. |
| [9] | 陈美霞, 金家坤, 彭旭, 等. 内、外壳对水下双层圆柱壳声振性能影响分析[J]. 船舶力学 , 2009, 13 (4) :628–634. |
 2016, Vol. 38
2016, Vol. 38
