2. 船舶与海洋工程水动力湖北省重点实验室,湖北 武汉 430074 ;
3. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Hubei Key Laboratory of Naval Architecture & Ocean Engineering Hydrodynamics, Wuhan 430074, China ;
3. Collaboration Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
由于数值模拟方法相对于实验方法拥有成本低、周期短、操作方便等一系列优点,故而计算流体动力学(CFD)应用十分广泛。
本文利用CATIA软件,以螺旋桨的投影原理和螺旋桨的相关型值参数为基础,建立三维螺旋桨模型。用Ansys icem建立相应流域、计算域,再划分非结构性网格。应用CFD软件(Ansys,Fluent),运用MRF技术,首先对螺旋桨的敞水性能进行数值模拟并将得到的结果与实验值对比,发现计算结果与实验结果测量值吻合良好。进而分析螺旋桨在敞水中的压力、速度分布。通过计算螺旋桨在不同情况的堵塞效应下的敞水性能,分析、研究堵塞效应的性质。并比较堵塞效应下与常态下螺旋桨的敞水性能,得到堵塞效应对于螺旋桨的敞水性能的影响,这对于研究螺旋桨的敞水性能具有一定的参考价值。
1 计算基本公式 1.1 RANS方程RANS方程是粘性流体运动学和动力学的普适性控制方程,本文用该方程作为求解螺旋桨水动力性能计算的基本方程。其具体方程式为:
| $ \begin{aligned} & \displaystyle\frac{{\partial (\rho {u_i})}}{{\partial t}} + \displaystyle\frac{{\partial (\rho {u_i}{u_j})}}{{\partial {x_i}}} = - \frac{{\partial p}}{{\partial {x_i}}} - \displaystyle\frac{\partial }{{\partial {x_j}}}(\rho \overline {u_i^′u_j^′} ) + \\ & \quad \quad \quad \rho {f_i} \!+\! \frac{\partial }{{\partial {x_j}}}\left[ {{\mu _o}(\displaystyle\frac{{\partial {u_i}}}{{\partial {x_j}}} \!+\! \frac{{\partial {u_j}}}{{\partial {x_i}}}) \!-\! \frac{2}{3}{\mu _o}\frac{{\partial {u_i}}}{{\partial {x_i}}}{\delta _{ij}}} \right]\text{。} \end{aligned} $ | (1) |
式中:ρ为流体密度;P为静压;fi为单位质量的质量力;ui,uj分别为速度分量。
1.2 湍流脉动动能方程湍流脉动动能方程即k方程:
| $ \frac{{\partial (\rho k)}}{{\partial t}} \!+\! \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} \!=\! {p_k} - \rho \varepsilon \!+\! \frac{\partial }{{\partial {x_j}}}\left[ {\left( {{\mu _o} \!+\! \frac{{{u_t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right]\text{。} $ | (2) |
雷诺应力模型是求解雷诺应力张量的各个分量的输运方程。具体形式如下:
| $ \begin{aligned} & \displaystyle\frac{{\partial (\rho \overline {{u_i}{u_j}} )}}{{\partial t}} + \frac{\partial }{{\partial {x_k}}}(\rho {U_k}\overline {{u_i}{u_j}} ) = \\ & \quad \quad \displaystyle\frac{\partial }{{\partial {x_k}}}\left[ {\rho \overline {{u_i}{u_j}{u_k}} + \overline {{\delta _{kj}}{u_i} + {\delta _{ki}}{u_j}} } \right] + \\ & \quad \quad \displaystyle\frac{\partial }{{\partial {x_k}}}\left( {\mu \frac{\partial }{{\partial {x_k}}}\overline {{u_i}{u_j}} } \right){\rm{ - }}\rho \left( {{{{u}}_{{i}}}{{{u}}_{{k}}}\displaystyle\frac{{\partial {{\rm{U}}_{{i}}}}}{{\partial {x_k}}}} \right){\rm{ - }}\\ & \quad \quad \rho \beta \left( {{g_i}\overline {{u_j}\theta } + {g_j}\overline {{u_i}\theta } } \right) + p\left( {\displaystyle\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) -\\ & \quad \quad 2\mu \overline {\displaystyle\frac{{\partial {u_i}}}{{\partial {x_k}}}\frac{{\partial {u_j}}}{{\partial {x_k}}}} - 2\rho {\Omega _k}\left( {\overline {{u_j}{u_k}} {\varepsilon _{ikm}} + \overline {{u_i}{u_k}} {\varepsilon _{jkm}}} \right)\text{。} \end{aligned} $ | (3) |
式中:Cij为对流项;Dijr为湍流扩散项;Dijl为分子扩散项;Pij为应力产生项;Gij为浮力产生项;øij为压力应变项;εij为耗散项,Fij为系统旋转产生项。
2 模型建立 2.1 螺旋桨投影原理DTMB4119桨是一种无侧斜无后倾分布的3叶螺旋桨,被ITTC选为考证数值方法预报精度的标准。其直径为0.304 8 m,螺距比为1.084,毂径比为0.2,剖面为NACA-66mod型。
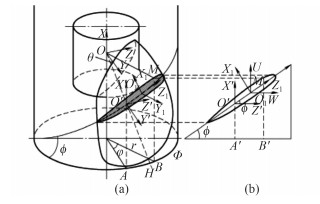
根据螺旋桨投影原理来建立模型(见图 1),首先将坐标系O1X1Y1Z1中的型值点经过一次旋转得到坐标系O1UVW中坐标,然后由坐标系O′X′Y′Z′与O1UVW的关系和图 1中平面坐标与图中柱坐标的关系,可推导出螺旋桨叶切面处局部坐标系O1X1Y1Z1到全局坐标系OXYZ的坐标变换公式为:
|
图 1 螺旋桨投影原理 Fig. 1 Propeller projection principle |
| $ \left[\!\! \begin{array}{l} X\\ Y\\ Z \end{array}\!\! \right] \!=\! \left[ \begin{array}{l} {Z_1}\sin \varphi + {X_1}\cos \varphi + L\sin \varphi - r\tan \theta \\[8pt] r\cos \left[ {\displaystyle\frac{{{Z_1}\cos \varphi - {X_1}\sin \varphi + L\cos \varphi }}{r}} \right]\\[8pt] r\sin \left[ {\displaystyle\frac{{{Z_1}\cos \varphi - {X_1}\sin \varphi + L\cos \varphi }}{r}} \right] \end{array} \right]\text{。} $ | (4) |
式中:θ为纵倾角,φ为螺距角;L为长度;r为切面所在圆柱面的半径。全局坐标系OXYZ的OXY平面与浆毂断面平行,坐标系与OXYZ平行,坐标系的轴经过叶切面的最厚处,坐标系经过一次旋转得到。
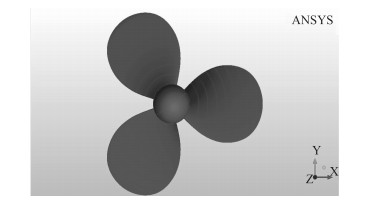
2.2 模型建造将以型值表形式表达的螺旋桨叶切面的局部坐标转换为全局坐标后,在CAD软件(本文使用CATIA)中进行三维建模,坐标轴的定义为:Z轴与螺旋桨旋转轴一致,来流方向指向z轴负向;X轴与桨叶参考线一致;Y轴服从右手系(见图 2)。计算时采用全尺模型,转速为20 r/s,通过改变进流速度来实现不同的进速系数下螺旋桨的计算。
|
图 2 螺旋桨模型 Fig. 2 The propeller model |
对于堵塞效应而言,由于需要研究起堵塞效应而导致螺旋桨敞水性能的变化,故而需要在螺旋桨前方、计算域内建立一个或者数个圆柱体来模拟堵塞固体块。本文建立以下2种对比模型:
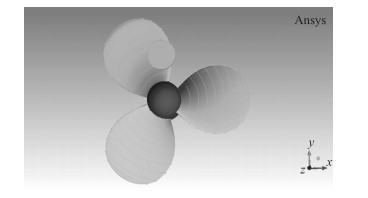
1)建一个半径为25 mm、高10 mm的圆柱体轴线平行z轴,其z轴正向圆柱表面圆心为(0,70,172.4),这是加1个堵塞物的模型(见图 3)。
|
图 3 添加1个堵塞物模型 Fig. 3 Add a blockage model |
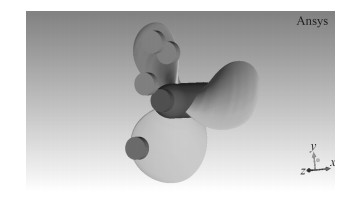
2)与上一模型类似,建立5个圆柱,半径为20 mm,高15 mm。其z轴正向圆柱表面圆心分别为(130,0,146.4),(80,100,250),(30,30,200.4),(80,80,200.4),(0,-80,200.4)。这是加5个堵塞物的模型(见图 4)。
|
图 4 添加5个堵塞物模型 Fig. 4 Add five blockage model |
对于CFD软件数值模拟来说,网格的划分是最为费时、费力的环节。因为该环节会影响到后来的计算,包括模拟计算的精度以及效率,网格过密或是过稀都会导致计算环节出问题。如果网格过于稀疏,则模拟精度不够,得到一个不准切的值,甚至是错误的结果。但若是网格过密,则会导致计算量增大,耗时过长,甚至无法收敛。
本文采用Ansys icem对螺旋桨划网格。局部加密,其余区域网格相对较稀,以便于计算。为模拟无限流畅,所建立的流域必须足够大,为方便计算,流域尺寸选取为螺旋桨直径的整数倍,故而建立一个直径为3倍的螺旋桨直径,长5倍的螺旋桨直径的圆柱体作为流域,其中螺旋桨距离流域來流部分为1倍直径,距尾部4倍直径。为模拟螺旋桨转动,贴近螺旋桨建立一个小的计算域,并运用MRF技术即相对旋转的原理,通过旋转坐标系来模拟螺旋桨的转动。其中小的计算域为直径为605.6 mm,长509.6 mm的圆柱。
为减小网格数目,故而设计流域网格密度较稀而计算域的网格相对较密,且在螺旋桨表面处加密。本文建立的都是非结构性网格。建立流域与计算域之间的区域为YU1,建立计算域与螺旋桨之间的区域为YU2。通过y-plus计算可得,螺旋桨第1层网格大小在1.6~6.3 mm之间。故而其他网格参数设定为YU1为流域,其最大网格尺寸为30 mm;YU2即为计算域,其最大网格尺寸为15 mm。而螺旋桨表面网格更小,设定最大网格尺寸为2 mm。
计算策略为:瞬态计算,计算模型选择湍流模型,入口以及流域壁面设定为速度入口,出口设定为水流出口。
4 计算结果分析 4.1 数值验证首先我们对Fluent软件计算螺旋桨敞水性能的准确性进行验证,表 1分别为通过Fluent软件计算以及船模试验所得的螺旋桨敞水实验数据。
|
|
表 1 螺旋桨敞水实验与计算数据对比 Tab.1 Data comparison of propeller open water test and calculation |
本文使用MRF动坐标系方法来模拟流动,用Fluent软件来进行流体计算。由表 1可知,桨敞水性能的数值模拟计算结果和试验结果相差不大。对于扭矩系数而言无论是单个还是总体误差均不大,其误差均在10%之内;推力系数误差最大其次为推进效率,除此之外误差在均不大。总的来说在所计算的case中,进速系数在0.5~1.1之间,Fluent数值模模拟的结果与实验值Kt,Kq,η分别在J等于0.833、0.9时吻合较好;当J=0.5、0.7时,Kt和η的误差略大,但总的来说平均误差在10%左右,在允许范围内。
由此可以得出结论,在误差允许范围内,Fluent数值模拟得到的螺旋桨敞水性能相应数值与实验值相同,即用数值模拟来求解螺旋桨的敞水性能的方法是可靠。
4.2 堵塞效应分析 4.2.1 固体块在垂直于螺旋桨轴线的面的运动的影响为研究这个问题,本文特地在加1个和5个固体块的模型中,对固体块设置边界条件为moving wall,且分别设置60 rad/s和125.6 rad/s速度旋转,进行Fluent计算。最后得出计算结果见表 2。在5个不同的case中,不论是推力还是扭矩相差均不大,推力相差在1%以内,而扭矩相差也很小。即转速的大小对其影响不大。故而可得出结论:堵塞固体块在垂直于轴线面上速度大小在一定范围内对螺旋桨的水动力性能影响不大。
|
|
表 2 固体块不同转速下螺旋桨推力、扭矩 Tab.2 Solid block at different speeds propeller thrust, torque |
理论上而言,对于流场,堵塞固体块越多对流场的影响越大,进而对螺旋桨的推力和扭矩影响越大。本文设定2种不同数量的堵塞固体块量,但堵塞固体块大小均相同。模型1代指只有1个堵塞固体块,模型2代指有5个堵塞固体块(具体建模见上文),其他条件保持一致,在Fluent中计算,具体结果如表 3所示。
|
|
表 3 堵塞效应下2种模型的推力以及扭矩 Tab.3 Thrust and torque at blocking effect of the two models |
由表 3可知,整体呈整体呈增大趋势,虽然计算的case有限,但趋势确定。即我们可确定在一定范围内随着堵塞固体块的增多,堵塞效应越严重,进而螺旋桨所受推力以及扭矩会增大。
4.2.3 堵塞效应对螺旋桨敞水性能的影响本文用模型2(即堵塞物较多的模型)对比螺旋桨敞水下数值,推力、扭矩对比如表 4所示。
|
|
表 4 螺旋桨在敞水及堵塞效应下的推力、扭矩 Tab.4 Thrust and torque of propeller in open water and clogging effects |
由表 4数据已看出加了固体快的模型在其他条件相同的情况下对应的推力和扭矩相对于普通的螺旋桨而言更大。即由4个计算的case可知堵塞作用下,螺旋桨的水动力载荷即推力和扭矩均增大,平均增量约为15%。
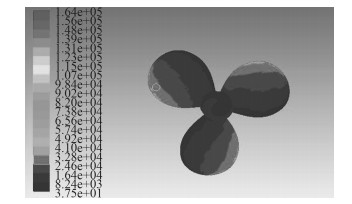
图 5和图 6分别为进速系数为0.7时敞水螺旋桨的压力云图,由图易得由于堵塞作用螺旋桨的桨叶叶面压力普遍高于敞水螺旋桨的叶面压力。与表中得出的结论一致,即堵塞效应下的螺旋桨对应推力、扭矩均有一定程度增大。本文计算的模型增大约为15%。

|
图 5 敞水螺旋桨压力云图 Fig. 5 Propeller open water stress nephogram |
|
图 6 堵塞作用下螺旋桨压力云图 Fig. 6 Stress nephogram of propeller under the plugging effect |
1)根据螺旋桨投影原理以及原始数据,利用CATIA软件建立4119桨的三维模型,实现了数据到模型的转化。
2)分析对比了数值模拟得到的数据以及实验得到的数据,发现在误差允许范围内数值模拟的结果与实验结果相同,验证了CFD数值模拟方法的可行性。并得到相应的误差范围。
3)对堵塞作用对于螺旋桨的影响做出来研究,分别研究了堵塞固体块的速度以及数量对螺旋桨敞水性能的影响,通过对比发现固体块在垂直螺旋桨旋转轴平面的速度对螺旋桨所受推力、扭矩影响不大;固体块的数量在一定范围内与螺旋桨的推力、扭矩成正比。为螺旋桨的研究提供了依据。
| [1] |
沈阅.螺旋桨非正常工作状态时的水动力性能研究[D].哈尔滨:哈尔滨工程大学, 2007.
SHEN Yue. The research on the characteristic of propeller in abnormal condition[D]. Harbin: Harbin Engineering University, 2007. http://www.cnki.com.cn/Article/CJFDTotal-KXJS201501022.htm |
| [2] |
高富东, 潘存云, 蔡汶珊, 等. 基于CFD的螺旋桨敞水性能数值分析与验证[J]. 机械工程学报 , 2010, 46 (8) :133–139.
GAO Fu-dong, PAN Cun-yun, CAI Wen-shan, et al. Numerical analysis and validation of propeller open-water performance based on CFD[J]. Journal of Mechanical Engineering , 2010, 46 (8) :133–139. DOI:10.3901/JME.2010.08.133 |
| [3] |
缪宇跃, 孙江龙. CFD敞水螺旋桨性能计算分析[J]. 中国舰船研究 , 2011, 6 (5) :63–68.
MIAO Yu-yue, SUN Jiang-long. CFD Analysis of hydrodynamic performance of propeller in open water[J]. Chinese Journal of Ships Research , 2011, 6 (5) :63–68. |
| [4] |
蔡荣泉, 陈凤明, 冯学梅. 使用Fluent软件的螺旋桨敞水性能计算分析[J]. 船舶力学 , 2006, 10 (5) :41–48.
CAI Rong-quan, CHEN Feng-ming, FENG Xue-mei. Calculation and analysis of the open water performance of propeller by CFD software Fluent[J]. Journal of Ship Mechanics , 2006, 10 (5) :41–48. |
| [5] |
刘帅.潜艇操纵运动水动力数值研究[D]上海:上海交通大学, 2011.
LIU Shuai. Numerical study of hydrodynamic forces on a maneuvering submarine[D] Shanghai: Shanghai Jiaotong University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10248-1011267880.htm |
| [6] |
孙存楼, 王永生, 李坚波. 基于CFD的调距桨调距过程桨叶水动力性能研究[J]. 哈尔滨工程大学学报 , 2010, 31 (2) :149–153.
SUN Cun-lou, WANG Yong-sheng, LI Jian-bo. Using CFD to analyze the hydrodynamic performance of controllable pitch propeller blades during pitch adjustments[J]. Journal of Harbin Engineering University , 2010, 31 (2) :149–153. |
| [7] |
王国栋.螺旋桨水动力、空泡和噪声性能预报方法研究[D].武汉:华中科技大学, 2013.
WANG Guo-dong. Investigation on the numerical simulation of propeller hydrodynamics、cavitation and noise[D]. Wuhan: Huazhong University of Science and Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10487-1014026280.htm |
| [8] |
王超.螺旋桨水动力性能、空泡及噪声性能的数值预报研究[D].哈尔滨:哈尔滨工程大学, 2010.
WANG Chao. The research on performance of propeller' hydrodynamics, cavitation and noise[D] Harbin: Harbin Engineering University, 2010. http://www.oalib.com/references/18936664 |
| [9] | SHAZLY M, PRAKASH V, LERCH B A. High strain rate compression testing of ice[M]. USA: National Aeronautics and Space Administration, Glenn Research Center, 2006 . |
| [10] | KASTEN M. Contmllahle pitch propellers[M]. UK: Kasten Marine Design, Inc., 1998 . |
 2016, Vol. 38
2016, Vol. 38
