当前,大多数驱护舰仍将动力系统排烟通道布置在上层建筑上,该位置出于飞行甲板前方,距离飞行甲板不远,尽管排烟速度不是很高,但是温度却明显高于环境空气[1],故它们对舰船甲板风的扰流作用不可忽视。在驱护舰的直升机着舰区域内,甲板风不仅流动是非稳态的,而且存在着复杂的涡结构,它们对直升机的安全起降具有非常大的影响,研究烟囱排烟对舰船甲板风特性的影响也具有十分重要的意义。舰船甲板风下洗流场对直升机安全起降影响较大,且主要是其脉动特性。
尽管试验方法是获得风流场脉动特性信息较为可靠的手段,但是现代驱护舰体型庞大,海上试验测量极其困难,故人们多采用风洞模型试验[2]。风洞试验确实具有很多优点。不过,也存在着一些突出的问题[3]:一是舰船模型需要缩小100倍以上,满足相似雷诺数的流动条件难以建立;二是全尺寸舰船的风扰动频率远大于缩比模型,不能真实地反映舰船甲板风的瞬间特性。从而,人们逐渐转用数值模拟方法来研究这一问题[4-6]。
当前,能获得流场高精度湍流脉动信息的模拟方法主要为大涡模拟方法(LES)和直接模拟方法(DNS),可是对于大型水面舰船甲板风这样属于高雷诺数的流动问题,采用DNS计算量将极大,目前不可能实现。为此,需要在计算精度和计算成本上折中考虑,本文采用LES方法模拟烟囱热排烟对舰船甲板风下洗效应的影响。
1 大涡模拟控制方程组大气绕流存在烟囱热排烟的水面舰船,是一个典型的低速空气流动问题,不考虑热烟气的热辐射效应和与空气间的化学反应,可以采用可压缩、无化学反应、无辐射、浮力驱动、低速流动的湍流瞬时控制方程组来描述。
考虑到本问题的气流速度较低,为了减小计算量,采用低马赫数假设[7],将气流压强分解为背景压强和速度诱导压强之和:
| $\bar{p}\left( x,t \right)={{\bar{p}}_{0}}\left( z \right)+\tilde{p}\left( x,t \right)$ | (1) |
假设气体压强、密度和温度满足理想气体状态方程,考虑大气分层,大气温度、大气密度和大气背景压强随高度变化为:
| $ {T_0}\left( z \right) = {T_a} + \varGamma z\text{,} $ | (2) |
| $ \frac{{{\rho _0}\left( z \right)}}{{{\rho _\infty }}} = \exp \left( { - \frac{g}{{R{T_0}}}z} \right)\text{,} $ | (3) |
| $ {\bar p_0} = {\rho _0}R{T_0}\text{。} $ | (4) |
式中:Ta为海面处大气温度;Γ为大气温度变化率。
应用盒式滤波器对控制方程组作Favre滤波运算,可得到大涡模拟的控制方程组为:
| $ \frac{{\partial \bar \rho }}{{\partial t}} + \nabla \cdot \bar \rho \tilde {\boldsymbol{u}} = 0 \text{,}$ | (5) |
| $ \bar \rho \left( {\frac{{\partial \tilde {\boldsymbol{u}}}}{{\partial {\boldsymbol{t}}}} + (\tilde {\boldsymbol{u}} \cdot \nabla \tilde {\boldsymbol{u}})} \right) + \nabla \bar p = \bar \rho {\boldsymbol{g}} + \nabla \cdot {\bar {\boldsymbol{\tau}} _l} + \nabla \cdot {\boldsymbol{\tau}} \text{,} $ | (6) |
| $ \begin{aligned} \displaystyle\frac{\partial }{{\partial t}}(\bar \rho {C_p}\tilde T) \!+\! \nabla \! \cdot\! (\bar \rho \tilde {\boldsymbol{u}}{C_p}\tilde T)\! =\! \frac{{{\rm D}\bar p}}{{{\rm D}t}} \!+\! \nabla \cdot (\lambda \nabla \tilde T) \!+\! \nabla \cdot {\boldsymbol{q}}\text{。} \end{aligned} $ | (7) |
计算时不直接求解上述方程(6)和方程(7),变化为:
| $ P = \frac{{{{\left| {\tilde {\boldsymbol{u}}} \right|}^2}}}{2} + \frac{{\tilde p}}{{\bar \rho }}\text{,} $ | (8) |
| $ \begin{array}{l} \displaystyle\frac{{\partial \tilde {\boldsymbol{u}}}}{{\partial t}} = \tilde {\boldsymbol{u}} \times \tilde {\boldsymbol{\omega}} + \frac{1}{{\bar \rho }}[(\bar \rho - {\rho _0}){\rm{g}} + \nabla \cdot {\boldsymbol{\tau}} ] + \\[8pt] \quad \quad \tilde p\nabla \left( {\frac{1}{{\bar \rho }}} \right) - \nabla P\text{,} \end{array} $ | (9) |
| $ \begin{array}{l} \displaystyle\nabla \cdot \tilde {\boldsymbol{u}} = \frac{1}{{\bar \rho {C_p}\tilde T}}\left[ {\nabla \cdot (\frac{{{\mu _T}{C_p}}}{{Pr}}\nabla \tilde T) - \tilde {\boldsymbol{u}} \cdot \nabla \left( {\bar \rho {C_p}\tilde T} \right)} \right] + \\[10pt] \quad \quad \quad \left( {\displaystyle\frac{1}{{{{\bar p}_0}}} - \frac{1}{{\bar \rho {C_p}\tilde T}}} \right)w{\rho _0}g\text{,} \end{array} $ | (10) |
| $ \begin{array}{l} {\nabla ^2}P = - \displaystyle\frac{\partial }{{\partial t}}\left( {\nabla \cdot \tilde {\boldsymbol{u}}} \right) + \nabla \cdot \left\{ {\tilde {\boldsymbol{u}} \times \tilde {\boldsymbol{\omega}} + \frac{1}{{\bar \rho }}[(\bar \rho - {\rho _0}){\rm{g}}} \right. + \\ \quad \left. {\begin{array}{*{20}{c}} {} & {} \end{array}\nabla \cdot {{\bar {\boldsymbol{\tau}} }_l} + \nabla \cdot {\boldsymbol{\tau}} ] + \tilde p\nabla \left( {\displaystyle\frac{1}{{\bar \rho }}} \right)} \right\}\text{,} \end{array} $ | (11) |
式中:τ和q分别为亚格子湍流应力和热流通量。对它们分别采用Deardorff亚格子模型[8]和涡扩散模型[9]进行模拟,并采用Werner-Wengle壁模型进行近壁区修正[10]。
在交错网格系上将上述大涡模拟控制方程组离散,时间上采用显式的2阶精度的预测-校正格式,空间上采用2阶精度的差分格式,对流项采用基于Superbee通量限制器的TVD格式,扩散项则采用中心差分格式。建立压强的Poisson方程(11)采用FFT方法直接求解。
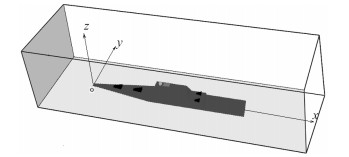
2 模拟对象与工况参数本文选取图 1所示的计算域,长600.0 m、宽400.0 m、高100.0 m。水面舰船模型位于计算域垂直对称面(y=0)上,舰首距离计算域入口150.0 m。舰船模型选取与美国“朱姆沃尔特”号接近的外形与尺寸,长183.0 m、宽24.0 m,机库后墙距离舰尾47.0 m,飞行甲板距离水面3.0 m。烟囱位于天线罩之后,出口与上层建筑平台平齐,开口形状为正方形,尺寸与上层建筑宽度一致,为4 m,其中心位于首尾线中央,即距离舰首91.5 m。
|
图 1 计算区域与舰船模型示意图 Fig. 1 The sketch map of simulated region and modeled ship |
计算中不考虑海浪的影响,也不考虑舰船的摇摆,假设海面为水平的固体壁面。在计算域入口(x=-100 m),给定风速条件,出口和垂直侧面采用自由边界条件,上表面采用滑移边界条件。在计算域的开口表面上,如果法向速度分量指向域外,则各变量取为自由边界条件,反之各变量则取为外界环境空气的参数。为模拟进口处的扰动,对速度边界条件加上随机噪声,并取随机噪声为均匀分布。计算中不考虑舰体与空气之间的热交换。
在各坐标方向上分别采用均匀网格划分,网格结点数目取为600 × 400 × 100。计算时间取为300.0 s,时间步长由CFL数确定。本文的计算采用大涡模拟软件FDS6.1进行[15, 16],该软件在国外已较多地用于风工程研究中并得到验证[17]。取海面处大气温度为20 ℃,Γ为-0.005 K/m。保持正向来风风向不变,来风速度取为10 m/s。假设排烟为热空气,排烟温度取为180 ℃,速度取为1.0 m/s。
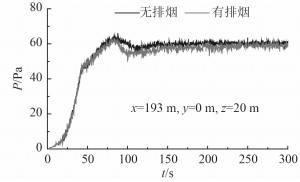
3 结果分析与讨论图 2为有无排烟条件下,飞行甲板后方某位置处压强的模拟结果,可以看出,t=150 s以后均达到了时均稳定,故时均数据处理的时间间隔为t=150~300 s。
|
图 2 飞行甲板后方某处的压强 Fig. 2 The calculated pressure of air at the point after the flight deck |
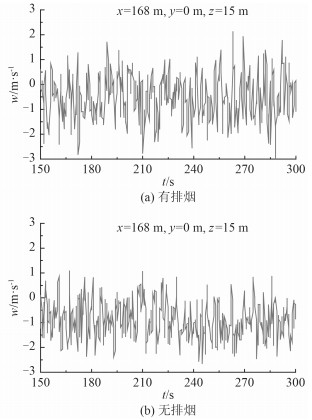
图 3给出了有无排烟条件下,飞行甲板首尾对称面上机库门附近某点(x=168 m,y=0,z=15 m)处下洗速度的模拟结果。由图可以看出,热排烟使该点下洗速度时均值略有降低,但是其脉动幅度有所增加。还可看出,有无热排烟,该点下洗速度均呈现出在时均值附近接近均匀脉动的随机变化。
|
图 3 飞行甲板上方首尾对称面上距离机库较近位置的下洗速度 Fig. 3 The calculated down-wash velocity of air flow at the point over the flight deck closer to the garage and on the ship bow-stern symmetrical plane |
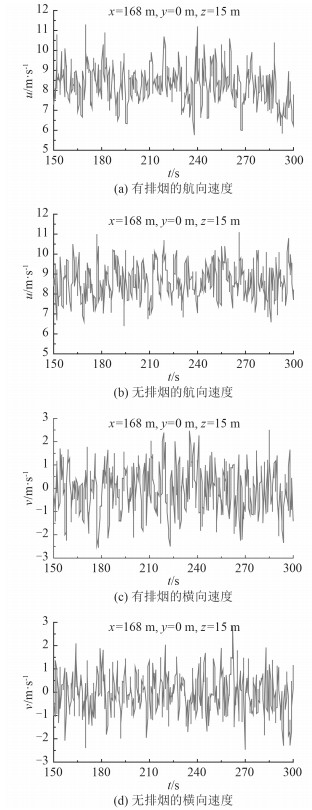
图 4给出了有无排烟条件下,飞行甲板首尾对称面上机库门附近某点(x=168 m,y=0,z=15 m)处航向和横向速度的模拟结果。由图可以看出,有无热排烟,该点航向速度变化所有不同,有热排烟时,该点航向速度接近周期性变化,而无热排烟时,则呈现出幅度接近对称的随机变化;有无热排烟,其航向速度的时均值差异不大,有热排烟时脉动幅度大于无热排烟时。对于横向速度,有无热排烟,该点横向速度的脉动值差异不大,有热排烟时略大于无热排烟。
|
图 4 飞行甲板上方首尾对称面上距离机库较近位置的航向与横向速度 Fig. 4 The calculated course and landscape velocities of air flow at the point over the flight deck closer to the garage and on the ship bow-stern symmetrical plane |
图 5给出了有无排烟条件下,飞行甲板左舷附近上方某点(x=168 m,y=-15 m,z=15 m)处下洗速度的模拟结果。由图可以看出,有无热排烟,该点下洗速度差异不大,均呈现出在时均值附近接近均匀脉动的随机变化,只是有热排烟时其脉动幅度略大于无热排烟时。

|
图 5 飞行甲板上方舷侧附近位置的下洗速度 Fig. 5 The calculated down-wash velocity of air flow at the point over the flight deck closer to the shipboard |
图 6给出了有无排烟条件下,飞行甲板左舷附近上方某点(x=168 m,y=-15 m,z=15 m)处航向和横向速度的模拟结果。由图可看出有无热排烟,该点航向速度基本相同,均呈现出在时均值附近幅度接近对称的随机变化,但是有热排烟时其脉动幅度略大于无热排烟时。对于横向速度,有无热排烟,该点横向速度的脉动值差异也不大,也只是有热排烟时略大于无热排烟。对比图 3~图 6还可看出,无论有无热排烟,飞行甲板上方侧舷附近的速度脉动均明显地低于首尾对称面上机库门附近的值。

|
图 6 飞行甲板上方舷侧附近位置的航向与横向速度 Fig. 6 The calculated course and landscape velocities of air flow at the point over the flight deck closer to the shipboard |
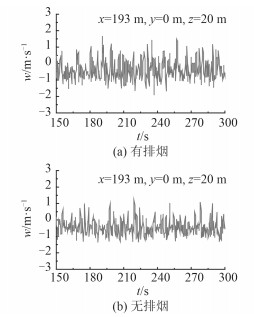
图 7给出了有无排烟条件下,飞行甲板首尾对称面上舰尾附近上方某点(x=193 m,y=0,z=20 m)处下洗速度的模拟结果。由图可看出,有无热排烟,该点下洗速度均呈现出在时均值附近接近均匀脉动的随机变化,其时均值基本一致,差异主要表现在其脉动幅度上,有热排烟时其脉动幅度大于无热排烟时。
|
图 7 飞行甲板上方艏艉对称面上舰尾附近位置的下洗速度 Fig. 7 The calculated down-wash velocity of air flow at the point over the flight deck closer to the stern and on the ship bow-stern symmetrical plane |
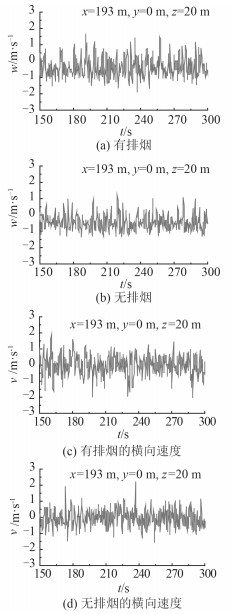
图 8给出了有无排烟条件下,飞行甲板首尾对称面上舰尾附近上方某点(x=193 m,y=0,z=20 m)处横向速度的模拟结果。由图可看出,有无热排烟,该点航向速度也均呈现出在时均值附近幅度接近对称的随机变化,时均值差异也不大,不过有热排烟时其脉动幅度大于无热排烟时。对于横向速度,有无热排烟,该点横向速度的脉动值差异也不大,也只是有热排烟时略大于无热排烟。对比图 3~图 8还可看出,无论有无热排烟,距机库门距离相同时,靠近首尾对称面区域的速度脉动均大于侧舷福晋区域,在首尾对称面上,飞行甲板上越靠近舰尾,速度脉动越小。
|
图 8 飞行甲板上方首尾对称面上舰艉附近位置的航向与横向速度 Fig. 8 The calculated course and landscape velocities of air flow at the point over the flight deck closer to the stern and on the ship bow-stern symmetrical plane |
本文采用低速气体流动控制方程组和湍流大涡模拟方法,对迎面来风条件下、有无热排烟条件下舰船飞行甲板风下洗特性进行了数值模拟研究,得到如下结论:
1)较无热烟气排出,热排烟使飞行甲板上方的下洗速度时均值减小,其脉动幅度增加;
2)飞行甲板上距离机库门相同的位置上,越靠近艏艉对称面,热排烟对下洗速度的影响越大;
3)越靠近舰尾区域,热排烟对飞行甲板风下洗速度的影响越小。
| [1] | 邵开文, 马运义. 舰船技术与设计概论[M]. 北京: 国防工业出版社, 2009 : 748 . |
| [2] | HEALEY J V. The Aerodynamics of ship superstructures[C]//Proceedings of AGARD Conference-aircraft Ship Operations., AGARD-CP-509, 1991. |
| [3] | POLSKY S A. A computational study of unsteady ship airwake[C]//AIAA 2002-1022, 40th AIAA Aerospace Sciences Meeting & Exhibit. Reno, Nevada: AIAA, 2002. http://www.oalib.com/references/17311430 |
| [4] | REDDY K R, TOFFOLETTO R, JONES K R W. Numerical simulation of ship airwake[J]. Computers & Fluids , 2000, 29 (4) :451–465. |
| [5] | VAN MUIJDEN J, BOELENS O J, VAN DER VORST J, et al. Computational ship airwake determination to support helicopter-ship dynamic interface assessment[C]//AIAA 2013-3078, 21st AIAA Computational Fluid Dynamics Conference, Fluid Dynamics and Co-located Conferences. San Diego, CA: AIAA, 2013. |
| [6] | SYMS G F. Simulation of simplified-frigate airwakes using a lattice-Boltzmann method[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2008, 96 (6/7) :1197–1206. |
| [7] | REHM R G, BAUM H R. The equations of motion for thermally driven, buoyant flows[J]. Journal of Research of the National Bureau of Standards , 1978, 83 (3) :297–308. DOI:10.6028/jres.083.019 |
| [8] | DEARDORFF J W. Numerical investigation of neutral and unstable planetary boundary layers[J]. Journal of Atmospheric Sciences , 1972, 29 (1) :91–115. DOI:10.1175/1520-0469(1972)029<0091:NIONAU>2.0.CO;2 |
| [9] | DEARDORFF J W. Stratocumulus-capped mixed layers derived from a three-dimensional model[J]. Boundary-layer Meteorology , 1980, 18 (4) :495–527. DOI:10.1007/BF00119502 |
| [10] | WERNER H, WENGLE H. Large-eddy simulation of turbulent flow over and around a cube in a plate channel[C]//Proceedings of the 8th Symposium on Turbulent Shear flows. Berlin Heidelberg: Springer, 1991, 34: 155-168. |
| [11] | MCGRATTAN K, HOSTIKKA S, MCDERMOTT R, et al. Fire dynamics simulator (version 6)-technical reference Guide[M]. NIST Special Publication 1018, 2013. |
| [12] | MCGRATTAN K, HOSTIKKA S, MCDERMOTT R, et al. Fire dynamics simulator (Version 6)-user's guide[M]. NIST Special Publication 1019, 2013. |
| [13] | MCGRATTAN K, HOSTIKKA S, MCDERMOTT J, et al. Fire dynamics simulator (version 6) technical reference guide volume 3: validation[M]. NIST Special Publication 1018, 2013. |
 2016, Vol. 38
2016, Vol. 38
