舰船螺旋桨发出的“唱音”是螺旋桨噪声中一种非常特别的噪声源,它的产生与流固之间强耦合作用密切相关,这种强耦合作用即为“锁定”现象。由于锁定现象涉及到流场和结构2个方面,其发生机理非常复杂。Philippe Ausoni等[1]以三维等直翼型为研究对象,进行不同来流速度下水动力性能和振动特性试验,试验成功捕捉到锁定现象,当涡脱落频率接近结构扭转固有频率时,结构振级达到最大,且在锁定雷诺数区间内,涡脱落频率均与结构固有频率保持一致。A.Zobeiri等[2]对不同随边形状三维等直翼在不同来流速度下的涡激振动特性进行了试验研究,试验结果表明,尖锐随边比更钝的随边更能降低锁定雷诺数区间内的振级,但对锁定频率大小及区间宽度影响较小。Eliasson R等[3]给出了相同来流速度不同随边形状翼型结构的振级,对称随边更有利于上下缘漩涡交替发放,从而激发较强的涡激振动;非对称随边则不利于漩涡的产生于发放,涡激振动振级较低。
弹性结构绕流锁定研究的难点在于计算方法,需要采用双向流固耦合方法进行计算。目前针对双向流固耦合算法的研究,主要方法有2种:一种是采用弹簧振子系统来模拟,结构被视为刚体;另一种是流场和结构同步求解,每一时间步交换耦合面上的力和位移,考虑了结构弹性对流场的反馈效应。
B.S. Carmo等[4]对不同来流速度下弹簧-圆柱系统振动特性进行了数值模拟,将得到的频率锁定区间划分为初始区域和稳定区域,在锁定区间内结构响应并未保持恒定,在初始区域内结构振级急剧上升达到峰值;而在稳定区域,振级逐渐下降。
随着大型计算机的发展以及数值计算软件的开发,双向流固耦合计算成为了可能。Gluck等[5]采用CSD和CFD数值算法软件包来同时进行结构和流场2个域的计算,通过MPCCI插值算法进行结构和流场两个独立耦合面节点之间位移和力的相互传递,从而将结构和流场2个域耦合在一起。Herwig Peters等[6]采用Workbench中的多物理场耦合模块对一端固支悬臂平板涡激振动进行了计算,研究了结构杨氏模量对悬臂板位移响应的影响规律。结果表明,当流体介质从空气变为水后,结构共振杨氏模量增加;结构在动水中共振杨氏模量相比于静水中杨氏模量并无显著差异。
文献[6]通过改变杨氏模量来研究锁定现象,工程应用性不强。本文在其算法的基础上,针对舰船螺旋桨经常出现的“唱音”现象,对一端固支柔性平板绕流进行了变来流速度的二维数值模拟,研究了其振动特性和水动力特性,对平板及翼型这类狭长结构绕流问题中常见的“锁定”现象发生机理进行研究,为螺旋桨“唱音”问题的解决提供参考。
1 双向流固耦合计算方法 1.1 初始流场控制方程本文流场介质为不可压黏性流体,且不考虑热交换,在当前雷诺数下,选用基于时间平均的湍流模型。具体方法是将湍流运动看做是时间平均流动和湍流脉动2种运动的线性叠加,因此,可将速度和压力进行如下处理:
| $ \left\{ \begin{array}{l} u = \bar u + u'\text{,}\\ v = \bar v + v'\text{,}\\ w = \bar w + w'\text{,}\\ p = \bar p + p'\text{。} \end{array} \right. $ | (1) |
式中:u,v,w为平均速度;u’,v’,w’为脉动速度;p为平均压力;p’为脉动压力。
将其代入瞬态的N-S方程,可得时均化的动量方程[7]:
| $ \left\{\!\!\!\! \begin{array}{l} \displaystyle\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\text{,}\\[10pt] \rho\displaystyle \frac{{\partial {u_i}}}{{\partial t}} \!\!+\! \rho \frac{\partial }{{\partial {x_j}}}({u_i}{u_j}) \!=\! \! -\! \frac{{\partial p}}{{\partial {x_i}}} \!\!+\!\! \frac{\partial }{{\partial {x_j}}}(\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} \!\!-\! \rho \overline {{{u'}_i}{{u'}_j}} ) \!+\! {S_i}\text{。} \end{array} \right. $ | (2) |
式中:
显然上式多了一个应力项,需要引入湍流模型以使其封闭。本文采用SST k-ω湍流模型,本模型是一个结合了k-ε的分区域湍流模型,在靠近壁面的边界层内使用k-ω模型,能更有效模拟较大的分离流动,而在远离边界层的自由流场中则使用k-ε模型,克服了k-ω对自由来流条件不太敏感的缺点,本模型是模拟平板绕流湍流运动的理想模型。
1.2 悬臂板振动控制方程悬臂板受迫振动有限元控制方程为:
| $ \begin{array}{l} {\boldsymbol{M}}\ddot w(x,y,z,t) + {\boldsymbol{C}}\dot w(x,y,z,t) + \\ \quad \quad {\boldsymbol{K}}w(x,y,z,t) = F(x,y,z,t)\text{。} \end{array} $ | (3) |
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;w为节点位移;F为平板表面分布激励力,即第1.1小节计算得到平板表面脉动压力。
1.3 双向流固耦合数据交换双向流固耦合的关键在于流场与平板之间的力和位移的相互传递,本文通过Ansys Workbench平台中的System Coupling模块来实现这种传递。首先求解1.1小节中初始流场(平板视为刚体),得到刚性平板表面脉动压力
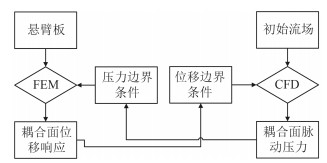
|
图 1 悬臂板双向流固耦合求解流程图 Fig. 1 Flow char of two-way fluid-structure interaction algorithm |
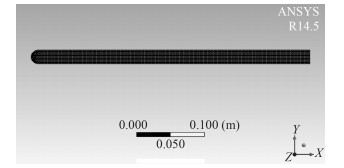
本文结构模型为二维弹性悬臂平板,其基本尺寸为:平板沿来流方向长L=0.41 m,平板厚度t=0.02 m,密度ρ=7 850 kg/m3,杨氏模量E=32 921 Pa,泊松比v=0.3。平板有限元模型采用solid186单元,如图 2所示,沿来流方向划分216份,沿厚度方向划分16份,沿展向划分1份,以模拟展向无限长平板,结构单元总数为3 586。
|
图 2 悬臂板有限元模型 Fig. 2 Finite element model of plate |
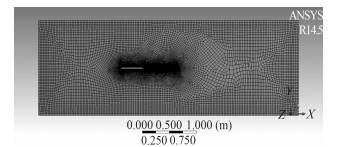
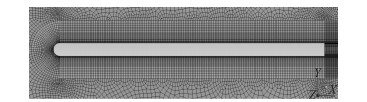
流体计算域如图 3和图4所示,流动方向为x轴正向,y轴方向为垂直于来流方向,左端流场入口边界到平板左端的距离为75倍板厚,出口边界到平板右端距离为140倍板厚,计算域上下边界到平板上下壁面的距离为40倍板厚。网格划分采用分块划分方法,结构近壁处采用加密的结构化网格,以更准确地模拟近壁面复杂的流动情况,远场则采用稀疏的非结构化网格,确保获得较快的计算速度。
|
图 3 全局流场网格 Fig. 3 Fluid domain |
|
图 4 近壁面网格 Fig. 4 Boundary layer |
入口边界条件:
出口边界条件:
平板表面及流域上下为无滑移固壁:u=0,v=0。
2.3 数值求解方法本文采用有限体积法来离散二维不可压缩非定常粘性流体控制方程(2),动量采用二阶迎风格式,时间项采用一阶隐式积分法,速度和压力耦合项采用Simple算法来求解。
3 弹性平板振动特性分析由于双向流固耦合计算十分缓慢,为了捕捉到平板锁定现象,在进行双向流固耦合计算之前,需要确定计算雷诺数区间。静水中悬臂平板第2、3阶固有频率分别为0.184 5 Hz和0.567 5 Hz,通过对刚性平板绕流进行试算,雷诺数为500和1 280时,涡脱落频率分别为0.185 7 Hz和0.561 8 Hz,与平板第2、3阶固有频率比较接近,因此,在500和1 280这2个雷诺数附近进行变速度双向流固耦合计算。
图 5给出了双向流固耦合算法下不同雷诺数悬臂板最大位移响应计算结果。图 5(a)为结构第2、3阶共振峰,图 5(b)为结构第二阶共振峰局部放大图。从图 5(a)可以看出,当雷诺数在500和1 280附近,平板发生极大的位移响应,这2个峰值工况对应的弹性平板尾部涡发放频率分别为0.186 4 Hz和0.557 3 Hz,与表 2中得到的静水中平板第2阶和第3阶固有频率基本吻合,在这2个雷诺数下,悬臂板被漩涡激发而产生共振。观察图 5(b),当雷诺数接近锁定区间时,悬臂板自由端位移响应缓慢增大到“位移平台”区,而当雷诺数超过锁定区间上限532时,结构位移响应迅速下降。

|
图 5 不同雷诺数下2种算法得到自由端总响应的对比 Fig. 5 Bending vibration amplitude of the free edge with different Reynolds number |
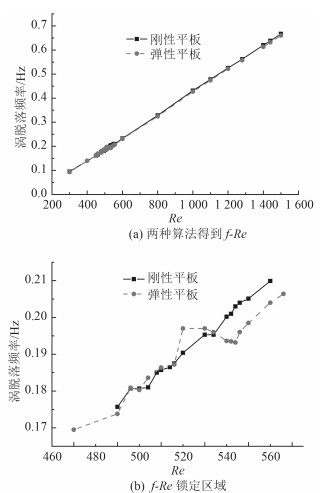
图 6(a)给出了刚性和弹性平板涡脱落频率随雷诺数的变化关系。图 6(b)给出了第2阶共振峰处的频率锁定区间。双向耦合算法在第2阶涡激共振区域捕捉到锁定现象,锁定雷诺数区间为520~532。在该区间内,涡脱落频率大体保持恒定,而刚性平板则不能得到这样的锁定区间。
|
图 6 刚性及弹性平板的涡脱落频率随雷诺数的变化规律的对比 Fig. 6 Vortex shedding frequency of the rigid and elastic plate at different Reynolds number |
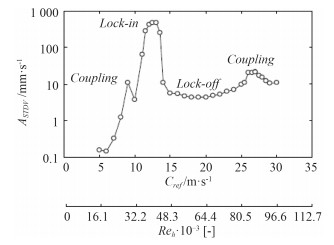
图 7为文献[14]中给出的某翼型绕流表面一点速度响应随雷诺数的变化曲线。本文得到的响应曲线与文献[14]翼型实验得到的曲线非常相似,规律基本一致。
|
图 7 某固定翼型绕流位移响应 Fig. 7 Vortex-induced vibration amplitude of a hydrofoil |
涡脱落频率与结构固有频率相一致为锁定发生的前提条件。表 1给出了平板固有频率及图 5(a)中2个峰值工况下涡脱落频率的对比。由表 1可知,当涡脱落频率接近结构某一阶固有频率时,漩涡将激发结构产生共振,此时流-固之间产生较强的耦合作用。
|
|
表 1 平板固有频率及对应峰值工况下涡脱落频率的对比 Tab.1 The second and third order natural frequency of the plate under water and votex shedding |
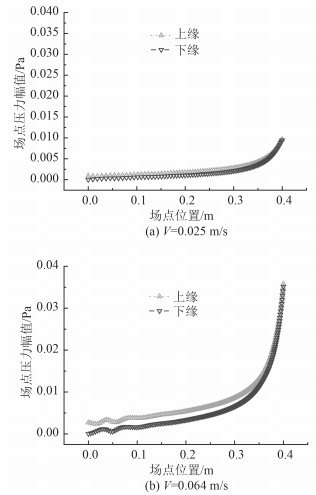
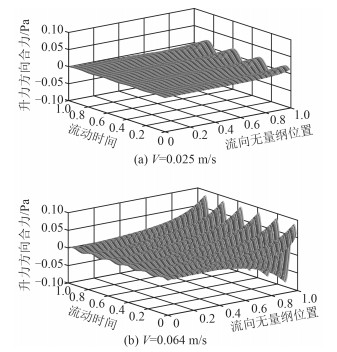
平板和翼型这类狭长结构更有利于涡激共振的产生,本质上是由于这种线型使得脉动压力的分布特性与结构固有模态发生高度吻合,从而激发结构与流场之间的强耦合作用,最终产生锁定。图 9所示为2个共振峰工况对应平板上下表面脉动压力幅值分布,从导边到随边,其幅值开始是缓慢增大,接近随边时则急剧增大,激励力主要集中在平板自由端,而其他区域则非常小,这是因为涡激振荡脉动压力完全由尾涡脱落而产生,漩涡主要在尾部形成,因此激励力也主要集中中尾端。图 10给出了平板法向脉动压力合力沿流向的时域分布,由图可知平板升力方向合力(激励力)幅值自导边至随边相位基本相同,而幅值则逐渐增大,与图 8(a)给出的结构第2阶固有模态分布更加匹配。

|
图 8 静水中平板第2,3阶模态云图 Fig. 8 The second and third order modes of the cantilever plate under water |
|
图 9 平板上下表面压力幅值分布 Fig. 9 The pressure distribution along the upper surface and the lower surface |
|
图 10 平板法向脉动压力合力时域分布 Fig. 10 Normal pressure in time domain |
从涡激振动幅值来看,图 5(a)中第2阶共振峰值明显小于第1阶的,而第2阶共振峰工况对应平板表面脉动压力明显大于第1阶,显然这是由于脉动压力分布特性与1阶共振峰处的固有模态更加吻合。在第2阶共振峰处,流-固之间耦合更加强,结构振级更高;而第3阶共振峰处,激励力分布与模态分布不再匹配,流固之间为弱耦合作用,结构振级较低。
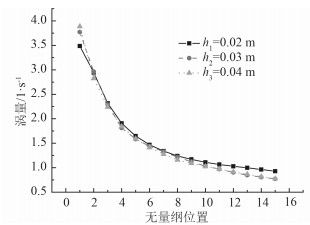
4.3 随边形状及尾涡强度条件涡激振动强度与脉动压力的幅值、相位与分布都密切相关,脉动压力则是由结构尾部上下缘漩涡周期性交替发放产生,而不同的尾部形状对漩涡的产生与脱落会产生重大影响。图 11所示为一刚性翼,弦长1 m,攻角为0,来流速度为0.5 m/s,分别对随边厚度为0.02 m,0.03 m和0.04 m三个刚性翼型进行绕流数值模拟。为了方便对比,各模型尾流场中涡量测点位置使用无量纲位置,3种模型涡量监测测点分别取在距离随边1~15倍随边厚度处。

|
图 11 翼型形状及尾流场测点分布 Fig. 11 Geometrical model and location of the measurement point in the wake |
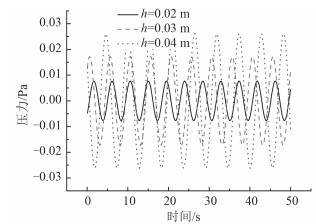
图 12给出了不同随边厚度翼型尾流场中涡脱落与耗散过程中,漩涡中心强度的对比。由图可知,相同来流速度下,较大的随边厚度翼型在近场将会形成强度较大的涡。钝翼尾涡强度明显强于尖翼,而随边处脉动压力幅值也更大,更容易激起结构极强的振动,如图 13所示。图 14所示为不同随边厚度模型涡量场,尾部越“尖锐”,越不易产生较强的漩涡发放;尾部越“钝”,则越有利于漩涡的产生与发放。
|
图 12 不同随边厚度模型对应涡强度的对比 Fig. 12 Vorticity magnitude of the foil with different thickness |
|
图 13 随边表面一点压力时间历程的对比 Fig. 13 The history of the pressure on the trailing edges with different thickness |

|
图 14 不同随边厚度模型对应涡脱落涡量云图 Fig. 14 Vortex arrangement along the wake of the trailing edges with different thickness |
本文采用计算流体力学方法和有限元方法来实现双向流固耦合,并以悬臂平板为研究对象,计算在不同雷诺数下,弹性平板的振动响应特性,成功捕捉到了频率锁定现象,并给出了锁定的形成条件,为螺旋桨唱音问题提供了指导方向,最终得到以下结论:
1)当悬臂平板尾部涡发放频率与静水中平板的固有频率相一致的时候,尾部漩涡的周期性发放将会诱导平板产生极大的振动响应。
2)涡与结构发生“锁定”现象,表现为结构位移响应峰值区域加宽,这是由于在共振频率附近区域,结构表面脉动压力幅值大小完全按结构模态分布,使得结构共振区域加宽。
3)结构和流场同时满足频率、压力分布和随边形状几个条件时,流-固之间将产生强耦合作用,结构振幅达到最大,流场涡脱落频率出现锁定现象,在此锁定区内,涡脱落频率保持不变,结构振幅也保持在一个很高的水平。而在其他固有频率处,虽能发生涡激共振,但振级大大低于锁定时的振级,此时流-固之间的耦合相对较弱。
| [1] | AUSONI P, FARHAT M, AIT BOUZIAD Y, et al. Kármán vortex shedding in the wake of a 2D hydrofoil: Measurement and numerical simulation[C]//IAHR int. Meeting of WG on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems. Barcelone, Spain, 2006. |
| [2] | ZOBEIRI A, AUSONI P, AVELLAN F, et al. How oblique trailing edge of a hydrofoil reduces the vortex-induced vibration[J]. Journal of Fluids and Structures , 2012, 32 :78–89. DOI:10.1016/j.jfluidstructs.2011.12.003 |
| [3] | ELIASSON R, LARSSON L, ORYCH M. Principles of yacht design[M]. A & C Black, 2014 . |
| [4] | CARMO B S, SHERWIN S J, BEARMAN P W, et al. Flow-induced vibration of a circular cylinder subjected to wake interference at low Reynolds number[J]. Journal of Fluids and Structures , 2011, 27 (4) :503–522. DOI:10.1016/j.jfluidstructs.2011.04.003 |
| [5] | GLÜCK M, BREUER M, DURST F, et al. Computation of fluid-structure interaction on lightweight structures[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2001, 89 (14/15) :1351–1368. |
| [6] | PETERS H, CHEN L, KESSISSOGLOU N. The effect of flow on the natural frequencies of a flexible plate[C]//INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Melbourne Australia: Institute of Noise Control Engineering, 2014: 610-616. |
| [7] | ANDERSON J D, WENDT J F. Computational fluid dynamics[M]. New York: McGraw-Hill, 1995 . |
| [8] | AUSONI P. Turbulent vortex shedding from a blunt trailing edge hydrofoil[D]. Lausanne: École Polytechnique Fédérale de Lausanne, 2009. http://biblion.epfl.ch/EPFL/theses/2009/4475/4475_abs.pdf |
 2016, Vol. 38
2016, Vol. 38
