起重船是一种海洋工程中常用的工程船舶,广泛应用于海上吊装、起重、铺管等作业。起重船作业过程中受到风浪作用产生运动,船体的运动会激励吊物产生摆动,吊物的摆动又会反过来产生一个附加动力载荷,大大增加船体的运动幅度,对起重船作业产生巨大的不利影响。
针对起重船船体和吊物的运动问题,国内外多位学者进行了大量研究,但目前的研究成果主要集中于环境载荷作用下吊物的摆动特性。Todd等[1]通过Stewart平台实验研究了吊物系统的摆动特性,并将吊物系统简化为球摆模型。Henry等[2]使用刚性无质量吊索和质量点组成的吊物系统研究了吊臂俯仰角变化对吊物摆动的影响。Chin,董艳秋和任会礼等[3-5]分别通过建立起吊过程中吊物摆动模型研究了吊物系统随吊索长度、起吊速度、浪向角、激励频率等变化的运动响应。任会礼等[6]通过建立刚柔耦合动力学模型研究了吊臂弹性对船体和吊物运动特性的影响。李跃等[7]通过建立起重船动力学模型研究了船体横摇运动和吊臂回转对吊物摆动的影响。王学林等[8]通过建立船舶和吊重耦合的多体动力学模型研究了规则波下和船体简谐运动时吊物运动轨迹。顾永宁等[9]推导了船体和吊物之间的运动传递函数,并计算了吊索附加动力载荷。
部分学者对船体和吊物的耦合运动特性进行了研究。Idres等[10]将船体与吊物视为统一整体并建立八自由度水动力模型研究了船体和吊物在起吊过程中的运动响应以及二者的相互影响。Schellin等[11]通过建立九自由度起重船模型研究了船体和吊物的运动响应并发现二者的耦合运动主要受一阶波浪力影响。陈新权等[12]在计算了吊索附加动力载荷的基础上计算了吊物运动对船体浮态和稳性的影响。汪涓娟等[13]通过三维势流理论建立起重船水动力模型研究了作业状态下起重船船体运动随吊索长度、吊重以及吊距的变化规律。魏国、何强[14-15]利用AQWA软件对spar平台吊装过程进行了数值模拟,其中何强将吊物运动的数值计算结果和试验结果进行了对比,二者吻合度良好。验证了AQWA软件用于起吊作业计算的可行性。
本文利用AQWA软件进行数值仿真,针对1艘12 000 t超大型全回转起重船,建立起重船和吊物的计算模型,考虑风浪流环境载荷,对不同吊臂旋转角、环境载荷入射角以及吊物重量情况下起重船作业状态下的运动响应。总结船体的运动变化规律以及船体和吊物运动的相互影响,为起重船作业过程提供依据。
1 计算理论 1.1 三维势流理论船体的运动方程为:
| $ \left( {{{\boldsymbol{m}}_{ij}} + {\boldsymbol{\mu} _{ij}}} \right){\ddot x_j} + {\boldsymbol{\lambda} _{ij}}{\dot x_j} + {{\boldsymbol{c}}_{ij}}{x_j} = {f_i}, \;i, j = 1, 2, \cdots 6。 $ |
式中:m和μ分别为质量矩阵和附加质量矩阵;λ为阻尼系数矩阵;c为回复力系数矩阵;f为波浪力;
三维势流理论假设速度势存在并满足Laplace方程和自由面条件、海底条件、物体湿表面条件和无穷远处边界条件4类边界条件。同时假设波浪运动和船体运动都是微幅的,则速度势可用叠加原理分解为入射势、辐射势和绕射势。入射势可采用线性波浪理论用Airy波速度势来表示。同时通过物体湿表面分布源汇的格林函数法得到物面辐射速度势和绕射速度势的积分方程为:
| $ \begin{align} & 2\text{ }\!\!\pi\!\!\text{ }{{\phi }_{j}}\left( X \right)+\frac{\partial G\left( \xi ;X \right)}{\partial {{n}_{\xi }}}\text{d}\xi =G\left( \xi ;X \right)\text{d}\xi \\ & 2\text{ }\!\!\pi\!\!\text{ }{{\phi }_{D}}\left( X \right)+\frac{\partial G\left( \xi ;X \right)}{\partial {{n}_{\xi }}}\text{d}\xi =4\text{ }\!\!\pi\!\!\text{ }{{\phi }_{0}}\left( X \right) \\ \end{align}。 $ |
式中:
按Bernoulli公式计算物体湿表面上的压力,将压力沿湿表面进行积分得到船体所受流体作用力,从而求解船体运动方程。
1.2 时域耦合分析根据Cummins脉冲响应方法,船体在某一时刻的运动可以归为一系列的瞬时脉冲运动的叠加,同时将波浪力分解为一系列脉冲响应的组合,由此可以将频域和时域计算联系起来,使得时域计算过程可以应用频率的计算结果。
时域分析中运动方程为:
| $ \begin{align} & \left\{ \boldsymbol{m}+{{A}_{\infty }} \right\}\ddot{X}(t)+c\dot{X}(t)+{{K}_{t}}X(t)+\int\limits_{0}^{t}{h(t-\tau )\ddot{X}(t)}\text{d}\tau = \\ & {{F}^{(1)}}(t)+{{F}^{(2)}}(t)+{{F}_{c}}(t)+{{F}_{w}}(t)+{{F}_{b}}(t)+{{F}_{t}}(t)+{{F}_{e}}(t) \\ \end{align}。 $ |
式中:
| $ h\left( t \right)=-\frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int\limits_{0}^{\infty }{}B\left( \omega \right)\frac{\sin \left( \omega t \right)}{\omega }\text{d}\omega =\frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int\limits_{0}^{\infty }{}\left\{ A\left( \omega \right)-{{A}_{\infty }} \right\}\cos \left( \omega t \right)\text{d}\omega $ |
式中A(ω),B(ω)分别为频域计算中波浪频率为ω时的附加质量和阻尼系数。
1.3 系泊缆动力分析对于系泊状态下的船舶,船体与系泊缆之间会相互影响,考虑二者的耦合作用能提高计算的可靠性。计入动态分析后,需要考虑系泊缆的质量、阻力、弹性张力和弯矩,可采用将系泊缆沿长度方向离散,将质量、系泊缆内力及外力集中于端点的方法计算系泊缆动态响应。
系泊缆单元的受力方程为:
| $ \begin{aligned} & \frac{{\partial {\boldsymbol{T} }}}{{\partial {s_e}}} + \frac{{\partial {\boldsymbol{V}}}}{{\partial {s_e}}} + w + {{\boldsymbol{F}}_h} = m\frac{{\partial {{\boldsymbol{R}}^2}}}{{\partial {t^2}}}\text{,}\\ & \frac{{\partial {\boldsymbol{M}}}}{{\partial {{\boldsymbol{S}}_e}}} + \frac{{\partial R}}{{\partial {{\boldsymbol{S}}_e}}} \times {\boldsymbol{V}} = - {\boldsymbol{q}}\text{。} \end{aligned} $ |
式中:m为系泊缆单位长度质量;q为单位长度上分布的力矩载荷矢量;R为系泊缆单元第一个点的位置矢量;∆Sε为系泊缆单元长度;Dε为系泊缆直径;w为系泊缆单元质量;Fh为系泊缆单元单位长度的水动力矢量;T为系泊缆单元第一个点的张力矢量;M为系泊缆单元第一个点的弯矩矢量;V为系泊缆单元第一个点的剪切力矢量。

|
图 1 系泊缆单元受力示意图 Fig. 1 Mooring cable force diagram |
弯矩和张力与材料的抗弯刚度EI和轴向刚度EA有关:
| $ \begin{aligned} & M = EI\frac{{\partial }}{{\partial {s_e}}} \times \frac{{{\partial ^2}}}{{\partial {s_e}^2}}\text{,}\\ & T = EA\varepsilon \text{。} \end{aligned} $ |
式中ε为系泊缆单元的轴向应变。
2 计算模型 2.1 水动力模型本文以1艘起重能力12 000 t的超大型全回转起重船为研究对象,其最大固定起重能力为12 000 t,全回转最大起重能力为7 000 t。根据实船资料建立计算模型,以重心在水线面上的投影为坐标原点,X轴以向船首为正方向,Y轴以向左舷为正方向,Z轴以向上为正方向。作业时起重船采取十点锚泊定位的方式,具体布置为船首左右舷各3根锚缆,船尾左右舷各2根锚缆,锚缆的布置根据环境载荷的变化而调整。主要尺度和模型见表 1和图 2。
|
|
表 1 起重船主要尺度 Tab.1 Ship principal dimension |
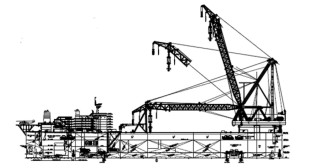
|
图 2 起重船总布置图 Fig. 2 General arrangement drawing of the ship |
建立研究对象的水动力计算模型如图 3所示,其水动力系数结果如图 4~图 5所示。
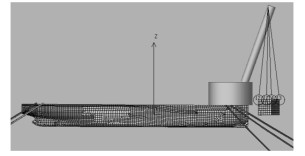
|
图 3 起重船水动力模型 Fig. 3 Hydrodynamic model of the ship |
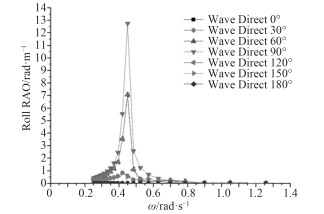
|
图 4 起重船横摇传递函数 Fig. 4 Roll RAO of the ship |
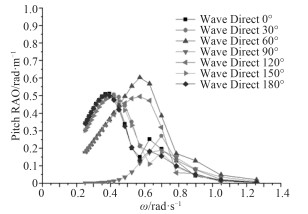
|
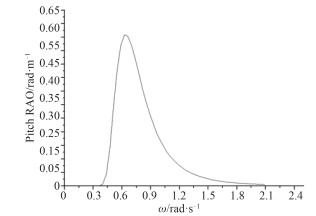
图 5 起重船纵摇传递函数 Fig. 5 Pitch RAO of the ship |
设计环境条件如表 2所示,不规则波谱为P-M波谱,如图 6所示。
|
|
表 2 计算环境条件 Tab.2 Environmental conditions |
|
图 6 P-M谱 Fig. 6 P-M spectrum |
对起重船在不同吊臂旋转角β、不同环境载荷入射角α及不同吊重工况下船体与吊物的耦合作用进行研究。
3.1 不同吊臂旋转角下船体和吊物的运动响应环境载荷入射角0°时船体运动响应时历曲线如图 7~图 9所示,1号系泊缆张力时历曲线如图 10所示,吊物运动时历曲线如图 11~图 13所示,计算结果汇总如表 3及图 14~图 17所示。
|
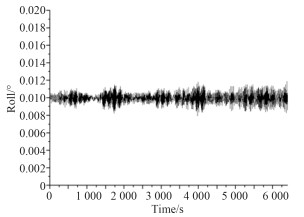
图 7 船舶横摇时历曲线 Fig. 7 Time history curves of roll |
|
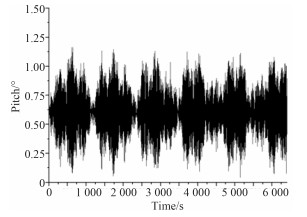
图 8 船舶纵摇时历曲线 Fig. 8 Time history curves of pitch |

|
图 9 船舶首摇时历曲线 Fig. 9 Time history curves of yaw |
|
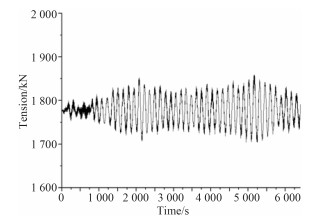
图 10 1号缆张力时历曲线 Fig. 10 Time history curves of tension of cable No.1 |
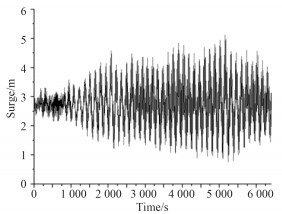
|
图 11 吊物纵荡时历曲线 Fig. 11 Time history curves of surge of load |
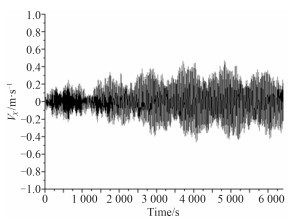
|
图 12 吊物纵向速度时历曲线 Fig. 12 Time history curves of longitudinal velocity of load |
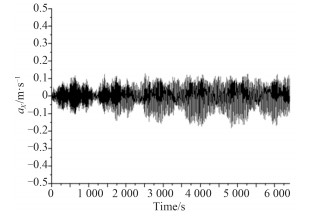
|
图 13 吊物横向加速度时历曲线 Fig. 13 Time history curves of longitudinal acceleration |
|
|
表 3 吊重7 000 t环境载荷入射角0°计算结果最大值汇总 Tab.3 The maximum value summary of calculation results when load weight is 7 000 t, αis 0° |
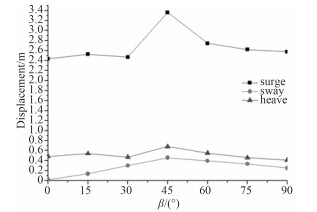
|
图 14 不同环境载荷入射角情况下船体位移极值曲线 Fig. 14 The change trend of ship displacement extreme value in different β |
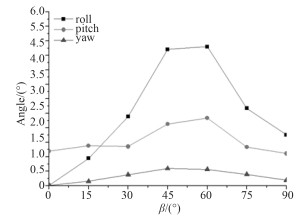
|
图 15 不同环境载荷入射角情况下船体位移极值曲线 Fig. 15 The change trend of ship displacement extreme value in different β |
|
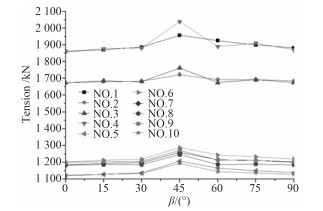
图 16 不同环境载荷入射角情况下缆绳张力极值曲线 Fig. 16 The change trend of mooring line tension in different β |
|
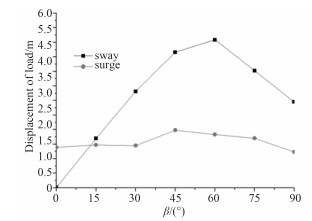
图 17 不同环境载荷入射角情况下吊物位移极值曲线 Fig. 17 The change trend of load displacement extreme value in different β |
从图 14~图 17可看出,船体横摇变化较大,且变化趋势为吊臂旋转角在从0°逐渐增大到45°或60°时,船体的横摇角逐渐增大,之后随着吊臂旋转角的增大船体横摇角逐渐减小。除横摇外的其余5个方向的运动响应及锚缆张力均变化较小,但变化趋势与横摇基本相同。吊物的摆动幅度与船体的横摇和纵摇幅度变化趋势相同,说明船体的运动与吊物的运动有很强的相关性,船体和吊物的运动相互影响。
3.2 不同环境载荷入射角α、不同吊重下船体和吊物的运动响应对起重船在相同系泊布置条件下环境载荷入射角0°,30°,60°,90°,120°,180°,固定起吊7 000 t,9 000 t,12 000 t重物时船体和吊物的运动响应进行了研究,计算结果见图 18~图 20所示。
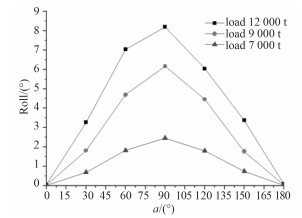
|
图 18 不同吊重、不同环境载荷入射角下船体横摇极值 Fig. 18 The change trend of ship roll extreme value in different α and different load weight |

|
图 19 不同吊重、不同环境载荷入射角下船体纵摇极值 Fig. 19 The change trend of ship pitch extreme value in different α and different load weight |
|
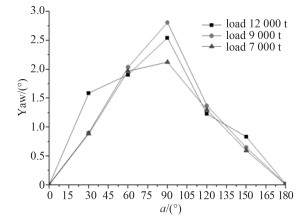
图 20 不同吊重、不同环境载荷入射角下船体艏摇响应 Fig. 20 The change trend of ship yaw extreme value in different α and different load weight |
从图 18~图 20可看出,环境载荷入射角0°~180°逐渐增大时,不同吊重下船体横摇和首摇都先增大后减小,并在环境载荷入射角90°时达到最大值。船体纵摇则呈现出先增大后减小再增大再减小的趋势,并在环境载荷入射角60°和120°时达到最大值,在环境载荷入射角90°时取得最小值。
当船舶吊重从7 000 t增加到12 000 t时,船体横摇随吊重的增大显著增大;船体首摇随吊重的增加变化不大;船体纵摇在吊重7 000 t和9 000 t时变化不大,而在环境载荷入射角0°~120°之间与吊重12 000 t时相差较大,出现这种情况的原因在于吊重12 000 t时吊臂旋转半径较大,导致船舶重心前移,使纵摇角度变大。
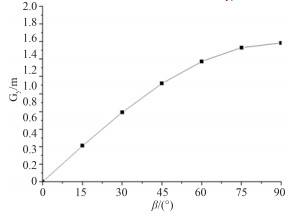
3.3 船体重心随吊臂旋转角变化大型起重船进行回转起重作业时,在作业前应进行预压载,作业过程中通过调节压载水以保证船舶的浮态。在本文计算过程中,考虑到不同吊臂旋转角下船舶的初始平衡性,以尽量减少船舶横摇为目标,分析重心横向位置变化对船舶运动和系泊系统的影响,得到在不同吊臂旋转角下船体重心横向位置(见图 21),可为作业过程中压载水调整提供参考。
|
图 21 重心横向位置 Fig. 21 Position of gravity center in y direction |
超大型回转起重船在作业过程中所受到的环境载荷和作业载荷的变化巨大,对船体和吊物的运动影响很大。本文针对系泊状态下起重船的运动响应进行了研究,建立了起重船的水动力模型,引入了风浪流环境条件,通过改变吊臂旋转角、环境载荷入射角和吊重,分析了起重船船体和吊物在不同条件下的运动响应,得到了以下结论,同时为起重船作业过程的操作提供了依据:
1)吊臂旋转角与中纵剖面的夹角为0°~90°时,随吊臂旋转角的增大,船体横摇变化最大,且变化趋势为先增大后减小,在吊臂旋转角45°或60°时取得最大值。其余5个方向的运动及锚缆张力变化较小,在吊臂旋转角45°或60°时取得最大值。
2)吊物的摆动幅值随吊臂旋转角的变化趋势为先增大后减小,并在吊臂旋转角45°时取得最大值,这与船体运动的变化趋势一致,且在船体横摇运动上表现最为明显。
3)环境载荷入射角0°至180°时,随环境载荷入射角的增大,船体的横摇和首摇先增大后减小,并在环境载荷入射角90°时取得最大值。船体纵摇变化趋势与吊重有关。
4)随环境载荷入射角的增大,船体横摇和首摇增加较快且幅值较大,因此在作业过程中要尽量使船舶处于迎浪或顺浪,避开横浪。
5)随吊重的增加,船体横摇逐渐增大,船体纵摇在部分环境载荷入射角下增大,而船体首摇变化不大。
6)考虑超大型起重船全回转作业过程中的浮态,分析重心横向位置变化对船舶运动的影响,确定作业过程中合适的重心位置,为作业过程中压载水调整提供参考,从而改善船舶全回转作业过程中的浮态。
| [1] | TODD M D, VOHRA S T, LEBAN F. Dynamical measurements of ship crane load pendulation[C]//Proceedings of MTS/IEEE Conference Proceedings. Halifax, NS:IEEE, 1997:1230-1236. |
| [2] | HENRY R J, MASOUD Z N, NAYFEH A H, et al. Cargo pendulation reduction on ship-mounted cranes via boom-luff angle actuation[J]. Journal of Vibration and Control , 2001, 7 (8) :1253–1264. DOI:10.1177/107754630100700807 |
| [3] | CHIN C M, NAYFEH A H, MOOK D T. Dynamics and control of ship-mounted cranes[J]. Journal of Vibration and Control , 2001, 7 (6) :891–904. DOI:10.1177/107754630100700607 |
| [4] |
董艳秋, 韩光. 起重船吊物系统在波浪中的动力响应[J]. 中国造船 , 1993 (1) :63–71.
DONG Yan-qiu, HAN Guang. Dynamic response of lifting load system of crane vessel in waves[J]. Shipbuilding of China , 1993 (1) :63–71. |
| [5] |
任会礼, 王学林, 胡于进, 等. 起重船吊物系统动力响应仿真分析[J]. 系统仿真学报 , 2007, 19 (12) :2665–2668.
REN Hui-li, WANG Xue-lin, HU Yu-jin, et al. Dynamic response simulation of lifting load system of ship-mounted cranes[J]. Journal of System Simulation , 2007, 19 (12) :2665–2668. |
| [6] |
任会礼, 王学林, 胡于进, 等. 考虑吊臂弹性的锚泊起重船动力特性研究[J]. 机械工程学报 , 2009, 45 (10) :42–47.
REN Hui-li, WANG Xue-lin, HU Yu-jin, et al. Dynamic response analysis of moored crane-ship with flexible booms[J]. Journal of Mechanical Engineering , 2009, 45 (10) :42–47. DOI:10.3901/JME.2009.10.042 |
| [7] |
李跃, 沈庆, 陈徐均. 波浪环境中作业起重船悬吊载荷的摆振分析[J]. 建筑机械 , 2003 (8) :55–57, 61.
LI Yue, SHEN Qing, CHEN Xu-jun. Swing analysis of suspended load of crane ship on the wave[J]. Construction Machinery , 2003 (8) :55–57, 61. |
| [8] |
王学林, 尤心一, 胡于进. 规则波作用下起重船吊重动力学仿真[J]. 中国机械工程 , 2010, 21 (9) :1077–1082.
WANG Xue-lin, YOU Xin-yi, HU Yu-jin. Cargo pendulation analysis of moored crane ship under regular waves[J]. China Mechanical Engineering , 2010, 21 (9) :1077–1082. |
| [9] |
顾永宁, 胡志强, 谢彬, 等. 大型起重船波浪诱导吊索附加动力荷载研究[J]. 中国海上油气 , 2005, 17 (3) :197–202.
GU Yong-ning, HU Zhi-qiang, XIE Bin, et al. Study on the additional dynamic load of lifting rope due to wave-induced motion of heavy crane barge[J]. China Offshore Oil and Gas , 2005, 17 (3) :197–202. |
| [10] | IDRES M M, YOUSSEF K S, MOOK D T, et al. A nonlinear 8-DOF coupled crane-ship dynamic model[C]//Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and materials conference. Norfolk, Virginia:American Institute of Aeronautics and Astronautics, 2003, 1855:4187-4197. |
| [11] | SCHELLIN T E, JIANG T, SHARMA S D. Crane ship response to wave groups[J]. Journal of Offshore Mechanics and Arctic Engineering , 1991, 113 (3) :211–218. DOI:10.1115/1.2919922 |
| [12] |
陈新权, 何炎平, 李洪亮, 等. 全回转起重船吊索动力荷载及其对浮态及稳性的影响[J]. 上海交通大学学报 , 2010, 44 (6) :778–781.
CHEN Xin-quan, HE Yan-ping, LI Hong-liang, et al. Study on the dynamic load of rope and its effect on floating and stability of revolving crane vessel[J]. Journal of Shanghai Jiaotong University , 2010, 44 (6) :778–781. |
| [13] |
汪娟娟, 黄衍顺, 李怀亮, 等. 吊重作业起重船波浪中的运动响应[J]. 中国舰船研究 , 2013, 8 (3) :50–57.
WANG Juan-juan, HUANG Yan-shun, LI Huai-liang, et al. Lifts' motion response in waves in the hoisting operation[J]. Chinese Journal of Ship Research , 2013, 8 (3) :50–57. |
| [14] |
魏国. Spar平台上部模块吊装过程中的碰撞响应分析[D].哈尔滨:哈尔滨工程大学, 2013.
WEI Guo. Collision response analysis during spar upper module installation[D]. Harbin:Harbin Engineering University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014132691.htm |
| [15] |
何强. Spar平台上层模块起吊运动数值分析[D].哈尔滨:哈尔滨工程大学, 2012.
HE Qiang. Numerical motion analysis for the lifting of spar upper module[D]. Harbin:Harbin Engineering University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012517334.htm |
 2016, Vol. 38
2016, Vol. 38
