2. 中国舰船研究设计中心, 湖北 武汉 430064 ;
3. 华中科技大学船舶与海洋工程学院, 湖北 武汉 430074
2. China Ship Development and Design Center, Wuhan 430064, China ;
3. Naval Architecture and Ocean Engineering, Hua zhong University of Sciences and Technology, Wuhan 430074, China
目前,对于空中爆炸的研究主要有理论分析、实船试验和数值仿真分析3类方法。现存很多空中爆炸相关理论主要由一些经验公式堆积而成,对基础理论的探讨还需要进一步加强。实船试验由于成本高、投入大、过程复杂、数据采集困难、保密等原因导致研究进展缓慢。相比之下,数值仿真具有成本低、周期短、模拟工况多等优点,所以目前研究工作主要依靠数值仿真。我国在舰船抗爆方面起步较晚,试验数据十分有限,且多数为水下爆炸冲击,在空气介质中的试验更为稀少。显式动力学有限元分析是动态特性分析中一种有效的数值分析方法,它为舰船在空爆载荷下的抗冲击性能仿真提供了新的方法。姚熊亮等[1]在研究空爆及舰船密闭舱室爆炸时改进了现有有限元程序,采用球面加载法得到冲击波压力。孔祥韶等[2]采用MSC.Dytran软件平台,实现了舱室内部爆炸的数值模拟。岳永威等[3]利用LS-DYNA模拟了空中爆炸载荷对典型军辅船结构的毁伤效果。刘紫嫣等[4]采用LS-DYNA对某舰船在空爆载荷下总强度进行分析。本文首先采用Ansys大型通用有限元软件对舰船整体结构进行完整建模并划分网格,然后利用LS-DYNA模拟了舱内爆炸环境下舰船结构的加速度响应,并和试验测得的数据进行对比,最终给出试验炸药当量下合适的仿真网格尺寸与边界条件,为舰船舱内空爆数值仿真方法提供参考。
1 材料参数及有限元模型 1.1 模型材料参数炸药单元采用欧拉网格,利用LS-DYNA中高爆炸药模型,通过EOS_JWL状态方程和MAT_HIGH_EXPLOSIVE_BURN材料模型描述炸药爆轰产物的状态,状态方程形式为:
| $ {P \!=\! A(1 - \frac{\omega }{{{R_1}V}}){e^{ - {R_1}V}} \!+\! B(1 - \frac{\omega }{{{R_2}V}}){e^{ - {R_2}V}} \!+\! \frac{{\omega E}}{V}}\text{,} $ | (1) |
式中:P为爆炸压力;V为相对体积;E为单位体积炸药内能;A,B,R1,R2,ω为JWL状态方程相关参数。TNT主要参数取值如下:A=3.71e11 MPa,B=3.23e9 MPa,R1=4.15,R2=0.95,ω=0.35,E=6e9 J/m3,ρ=1 630 kg/m3,V=1,D=6 930 m/s。空气采用欧拉网格,利用线性多项式方程*LNIEAR_POLYNOMIAL MODEL和空白材料*MAT_NULL来描述其流动状态。状态方程形式为:
| $ {P \!=\! {C_0} \!+\! {C_1}\mu \!+\! {C_2}{\mu ^2} \!+\! {C_3}{\mu ^3} \!+\! ({C_4} \!+\! \\ {C_5}\mu \!+\! {C_6}{\mu ^2})E}\text{,} $ | (2) |
式中:C0,C1,C2,C3,C4,C5,C6均为用户定义的常量;E为初始能量;μ=1/V -1,V为相对体积。空气流场主要参数取值如下:C0=-1.0e5 Pa,C1=C2=C3=C6=0,C4=C5=0.4,E=2.5e5 Pa,V0=1,ρ=1.29 kg/m3。船体结构采用拉格朗日网格,利用JOHNSON-COOK塑性模型[5]描述,该材料流动应力为:
| $ \sigma = (A + B{\overline \varepsilon ^p}^n)(1 + C\ln {\dot \varepsilon ^*})(1 - {T^*}^m)\text{,} $ | (3) |
式中:A,B,C,n,m均为材料常数;A为屈服应力,B为应变硬化系数;C为应变率敏感系数;m为温度敏感系数;
船体结构有限元模型中,爆炸中心及相邻舱段网格尺寸为75 mm[6],其余舱段网格随距爆炸中心距离增大而增大,单元总数为383 731个,船体结构有限元模型如图 1所示。考虑到爆炸位置位于第3、第4舱室之间,仅建立船体首部上层建筑,其余舱段通过调整外板密度使之和实船各舱段总重量一致。水线面下方结构采取等效密度方式以弥补附连水质量,附连水质量采用里维斯法[7]进行计算,约为舰船整体质量的2.23倍。

|
图 1 船体有限元模型示意图 Fig. 1 Finite element model of vessel |
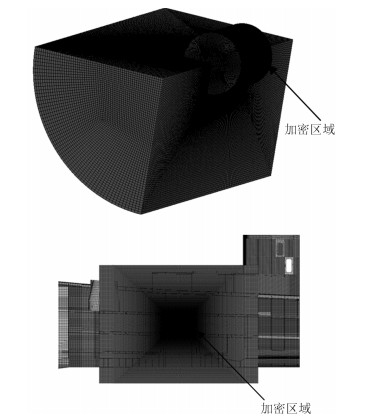
假设空气为连续介质,综合考虑计算精度与计算成本,以炸药为中心,半径为7 m,长度为18 m的圆柱体作为空气域的大小,将爆炸中心舱室及相邻两舱室包裹在内。此外,对以炸药为中心,半径1.2 m长度3 m的圆柱体内网格进行局部加密,使冲击波不易衰减。局部加密网格尺度分别取125 mm,75 mm和20 mm计算冲击波载荷,流场采用无反射边界条件。空气流场有限元模型如图 2所示。空气与炸药使用关键字*ALE_MULTI-MATERIAL_GROUP绑定在同一算法里,使二者可以进行物质交换和运输。流体(Euler网格)和船体结构(LAGRANGE网格)采用*CONSTRAINED_LAGRANGE_IN_SOILD关键字实现的耦合[8]。
|
图 2 空气流场有限元模型示意图 Fig. 2 Finite element model of air field |
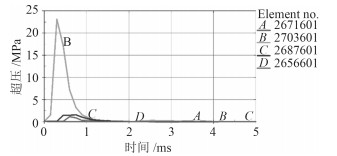
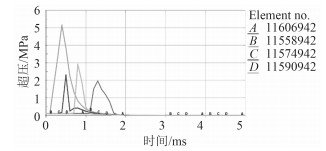
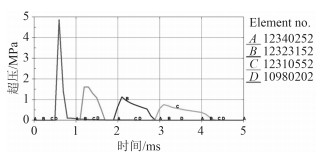
冲击波在空气中传播,较水中传播速度慢,峰值压力低,衰减快[9],不同TNT当量采用不同密度的网格才能精确地模拟空气中冲击波的传播[10]。图 3~图 5为120 kg TNT炸药当量下网格尺寸分别为125 mm,75 mm和20 mm下数值仿真所得冲击波时间历程曲线。
|
图 3 125 mm网格尺寸爆炸冲击波 Fig. 3 Shock wave of 125 mm grid |
|
图 4 75 mm网格尺寸爆炸冲击波 Fig. 4 Shock wave of 75 mm grid |
|
图 5 20 mm网格尺寸爆炸冲击波 Fig. 5 Shock wave of 20 mm grid |
取Henrych公式[11]中折算距离为参考依据,将图 3~图 5中所得数据列于表 1中并与Henrych经验公式对比,表中冲击波超压峰值取小数点后2位。
|
|
表 1 冲击波压力峰值统计表 Tab.1 Peak pressure of shock waves |
结合图表可看出,随着折算距离的增大,仿真结果与经验公式误差越小。网格尺寸为125 mm和75 mm时,接近爆心部分的冲击波峰值不能得到有效的模拟。网格尺寸为20 mm时,冲击波观测点超压峰值误差在10%之内,符合本模型的计算要求。
2.2 结构边界约束条件模拟在实船靶试验中,舰船受爆炸冲击载荷外还受重力和浮力的作用,无明确边界条件。本模型假定了2种边界约束条件:1)无约束边界条件;2)约束舰船尾封板;通过对这2种边界条件的计算结果进行对比,选取其中一种作为全船数值仿真的边界条件。
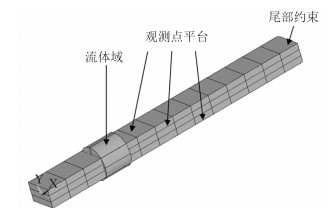
建立如图 6所示的长120 m,宽12 m,高8 m与实船尺寸相近的矩形简化结构,并将该矩形模型按长度均分为14段,每个分段再按高度均分为3个分段。流场几何尺寸与图 2中一致,爆炸位置位于第4~第5个横向分段。由于只观测约束对结构加速度响应的影响,为了减少计算时间及网格划分难度,结构网格尺寸设为500 mm,流场内部单元尺寸为50 mm,外部渐疏,最外边缘单元尺寸为300 mm,同时加大爆炸计算当量使其出现明显加速度。
|
图 6 约束条件简化模型 Fig. 6 Simplified model for constraint |
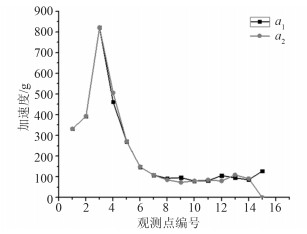
第1种边界条件未做任何约束,第2种边界条件在图 6中尾部进行刚性固定。观测点所在平面如图 6所示,分别对应于实船的上甲板、下甲板、船底板部分。选取各分段平面的中点,每层平面皆有14个观测点,得到数据如图 7~图 9所示。其中,a,b,c分别为第1,2,4层,1为无约束数据,数据点为方形,2为尾封板约束数据,数据点为圆形,横坐标为观测点沿长度方向编号,垂向坐标轴为加速度,单位为g。
|
图 7 第1层平台加速度对比 Fig. 7 Acceleration of first platform |
|
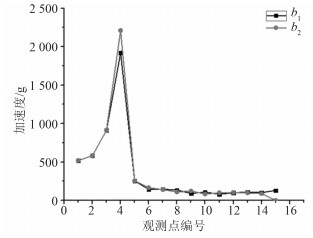
图 8 第2层平台加速度对比 Fig. 8 Acceleration of second platform |
|
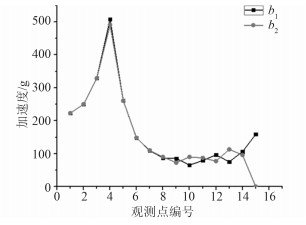
图 9 第4层平台加速度对比 Fig. 9 Acceleration of last platform |
对比可知,第1层和第4层在模型前半段加速度分布基本一致,后半段有较大偏差;第2层仅在峰值最大处有15%左右的偏差;最后1个观测点由于约束的原因3层偏差较大。从整体来说,尾端约束与无约束2种边界条件对结构加速度响应的结果相近,考虑到实际情况中尾部加速度并不为0,采用无约束边界条件较尾端约束更接近实际情况。
3 数值模拟计算结果以图 10上甲板观测点为例,本模型加速度观测点从#0开始,取每隔5 m处该结构中线面上的点。观测点分别分布在上甲板、下甲板、1号平台和中龙骨上。此外,爆炸及相邻舱段观测点加密。爆心位于距船首25 m处下甲板和1号平台之间,TNT当量120 kg。数值仿真得到部分观测点加速度结果列于表 2中,表中“--”表示该肋位无相应结构。

|
图 10 观测点分布示意图 Fig. 10 Distribution of observation point |
|
|
表 2 加速度峰值列表 Tab.2 List of peak acceleration |
根据观测点数据得到图 11~图 14的加速度分布曲线。图中横坐标为距船首沿船长距离,单位为m,纵坐标为加速度,单位为一个重力加速度g,0 m为船首#0处。可以看出,15 m~40 m段船体加速度变化明显,最大加速度可达1.0E5 g数量级,船首船尾加速度基本在1.0E1 g数量级,大致分布列于表 3中。
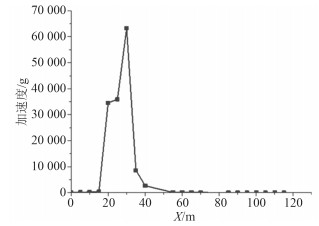
|
图 11 上甲板加速度峰值分布 Fig. 11 Peak acceleration of upper deck |
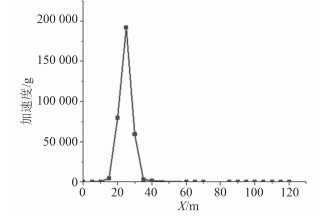
|
图 12 下甲板加速度峰值分布 Fig. 12 Peak acceleration of lower deck |
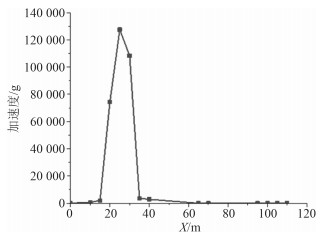
|
图 13 一号平台加速度峰值分布 Fig. 13 Peak acceleration of platform 1 |
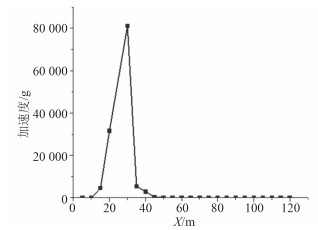
|
图 14 龙骨加速度峰值分布 Fig. 14 Peak acceleration of keel |
|
|
表 3 船体结构加速度峰值大致分布表 Tab.3 Distribution of peak acceleration |
取距离爆心不同水平位置观测点的数值模拟结果与实验数据作对比,结果列于表 4中。仿真数据和实验结果对比表明,在流场范围内观测点的仿真加速度峰值与实验加速度峰值误差较小,距离爆心较远处误差较大,这是由于流场大小和远处网格尺寸较粗糙导致的。
|
|
表 4 实验与数值模拟结果对比 Tab.4 Comparison of experiments and numerical simulation |
本文采用Ansys/LS-DYNA对某大型水面舰船在空爆载荷作用下响应进行了数值仿真分析。在考虑附连水作用下,通过对不同流域网格尺寸和不同边界条件进行仿真计算,并分别与经验公式和实测值进行比较,得到如下结论:
1)对比经验公式超压值可得到不同炸药当量下合适的网格尺寸。20 mm网格尺寸可以较好地模拟120 kgTNT在空气中的爆炸冲击波,观测点超压误差在10%以内。
2)将船尾进行全约束和无约束边界条件对比可知,全约束的边界条件仅对约束附近加速度峰值有较大影响,其他部位两者加速度峰值基本一致,因此采用无约束边界条件与试验情况更为接近。
3)由数值仿真和实验测量加速度对比可知,在流场范围内观测点的仿真加速度峰值与实验加速度峰值误差较小,距离爆源较远处误差较大,这主要由于远处网格尺寸较粗糙导致的。
| [1] |
张秀华, 张达.基于Euler算法的TNT炸药空中爆炸数值模拟研究[C]//第23届全国结构工程学术会议论文集.兰州:中国力学学会, 2014.
ZHANG Xiu-hua, ZHANG Da. Blast shock wave characteristics and propagation law of internal gas explosion[C]//The Corpus of 23th National Structural Engineering Academic Meeting., Lanzhou: Chinese Society of Mechanics, 2014. |
| [2] |
孔祥韶, 吴卫国, 李晓彬, 等. 舰船舱室内部爆炸的数值模拟研究[J]. 中国舰船研究 , 2009, 4 (4) :7–11.
KONG Xiang-shao, WU Wei-guo, LI Xiao-bin, et al. Numerical simulation of cabin structure under inner explosion[J]. Chinese Journal of Ship Research , 2009, 4 (4) :7–11. |
| [3] |
岳永威, 王超, 王奂钧. 计及水流场效应的军辅船空爆毁伤特性[J]. 舰船科学技术 , 2013, 35 (1) :16–21, 64.
YUE Yong-wei, WANG Chao, WANG Huan-jun. Research on damage effect of military auxiliary vessels subject to the air explosion load considering water flow[J]. Ship Science and Technology , 2013, 35 (1) :16–21, 64. |
| [4] |
刘紫嫣, 王超, 岳永威, 等. 空爆载荷作用下舰船结构总强度分析[J]. 舰船科学技术 , 2012, 34 (12) :46–50.
LIU Zi-yan, WANG Chao, YUE Yong-wei, et al. Total strength analysis of warship structure under air explosive load[J]. Ship Science and Technology , 2012, 34 (12) :46–50. |
| [5] | JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]// Proceedings of the 7th International Symposium on Ballistics. Netherlands: The Hague, 1983. http://www.oalib.com/references/16161704 |
| [6] |
江帆.空爆载荷作用下舰船结构动态响应研究[D].哈尔滨:哈尔滨工业大学, 2011.
JIANG Fan. Research on dynamic response of warship structure under explosion loading in the air[D]. Harbin: Harbin Engineering University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012264453.htm |
| [7] | 金咸定, 夏利娟. 船体振动学[M]. 上海: 上海交通大学出版社, 2011 . |
| [8] | LSTC. LS-DYNA keyword user's manual, version 971[Z]. LSTC, 2005. |
| [9] |
张社荣, 李宏璧, 王高辉, 等. 空中和水下爆炸冲击波数值模拟的网格尺寸效应对比分析[J]. 水利学报 , 2015, 46 (3) :298–306.
ZHANG She-rong, LI Hong-bi, WANG Gao-hui, et al. Comparative analysis of mesh size effects on numerical simulation of shock wave in air blast and underwater explosion[J]. Journal of Hydraulic Engineering , 2015, 46 (3) :298–306. |
| [10] |
张秀华, 张达.基于Euler算法的TNT炸药空中爆炸数值模拟研究[C]//第23届全国结构工程学术会议论文集.兰州:中国力学学会, 2014.
ZHANG Xiu-hua, ZHANG Da. Blast shock wave characteristics and propagation law of internal gas explosion[C]//The Corpus of 23th National Structural Engineering Academic Meeting., Lanzhou: Chinese Society of Mechanics, 2014. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-LXFY201410003047.htm |
| [11] | 亨利其J.爆炸动力学及其应用[M].熊建国, 译.北京:科学出版社, 1987. |
 2016, Vol. 38
2016, Vol. 38
