2. 中国人民解放军91388部队, 广东 湛江 524022
2. No.91388 Unit of PLA, Zhanjiang 524022, China
利用混沌系统进行微弱信号检测的基本原理是混沌系统具有对噪声及与其内置信号频差较大信号免疫,而对与混沌系统内置信号频差较小信号敏感的特点[1-5]。
当混沌系统处于由混沌状态转化为大尺度周期状态的临界状态时,若输入噪声则系统仍保持混沌状态,而输入与之同频率的微弱信号,则系统迅速进入大尺度周期状态,据此可以检测待测信号中是否含有微弱信号[6-10]。
在混沌微弱信号检测中,如何确定混沌临界值至关重要[11]。仿真中发现:选取不同精度的临界值将影响混沌系统的检测性能,本文主要研究不同精度的临界值将如何影响系统的检测性能。
1 混沌系统微弱信号检测的基本原理考虑可用于任意频率微弱信号检测的duffing混沌检测系统,其duffing方程为:
| $ \ddot{x}=-k\omega \dot{x}+{{\omega }^{2}}\left(x-{{x}^{3}}+\gamma \text{cos}\left(\omega t \right)\right)\text{, } $ | (1) |
式中,ω和γ分别为混沌系统内置信号频率和幅度;k为阻尼系数,一般取k=0.5;(x-x3)为非线性项;
随着γ值的变化,系统的相轨迹将发生变化,历经同宿轨道、倍周期分叉轨道、混沌状态及大尺度周期状态等,当γ等于混沌临界阈值γd时,系统进入混沌临界状态。此时若输入纯噪声,系统仍保持混沌状态,若输入含有与内置信号频率相同的信号时,系统迅速从混沌状态转化为大尺度周期状态,据此可检测微弱信号是否存在。
2 混沌系统临界阈值的确定Lyapunov指数可用于定量确定系统的状态和混沌临界值:系统的最大Lyapunov特性指数大于0,说明系统处于混沌状态;当系统的最大Lyapunov特性指数小于0时,说明系统处于大尺度周期状态;当Lyapunov特性指数由大于0转为小于0,则说明系统从混沌态跃变到了周期态,最大Lyapunov特性指数符号转变的那一刻所对应的系统内置信号幅值即为系统临界阈值。文献[12]中给出了Lyapunov指数的具体计算方法及利用该指数计算系统临界阈值的方法。
以ω=1为例,取系统初始值
|
|
表 1 11个采样点对应的Lyapunov指数值 Tab.1 Lyapunov characteristic exponents corresponding to 11 sample points |
由表 1可知,小数点后取3位的混沌临界阈值为γd=0.825,由图 1中γ=0.825和γ=0.826对应的时域图和相轨迹图也可以判定0.825是混沌临界阈值。

|
图 1 系统对应的时域图和相轨迹图 Fig. 1 Time-domain diagram and phase contrail diagram of chaotic system |
若要取更高精度的临界阈值,则可将[0.825,0.826]以0.000 1为步长进行等分,同样计算各采样点对应的Lyapunov指数,根据Lyapunov指数值得到更高精度的临界阈值,得到其精度取小数点后4位对应的临界阈值为0.825 8。该过程一直持续下去,直到得到预先设置的精度。这里以小数点后8位为设置精度,得到各采样点对应的Lyapunov指数如表 2所示。
|
|
表 2 12个采样点对应的Lyapunov指数值 Tab.2 Lyapunov characteristic exponents corresponding to 12 sample points |
由表 2可知,小数点后取8位对应的混沌临界阈值为γd=0.825 843 00。
3 不同精度的临界值对检测性能的影响由第2节可知式(1)中的duffing混沌系统的临界阈值按不同精度可取为0.82,0.825,0.825 8和0.825 843 00。
3.1 只输入高斯白噪声时对混沌系统检测性能的影响将duffing系统处于混沌临界状态,即将式(1)中的γ分别取为0.82,0.825,0.825 8,0.825 843 00时,在系统中加入高斯白噪声,式(1)变为如下形式:
| $ \ddot{x}=-k\omega \dot{x}+{{\omega }^{2}}\left(x-{{x}^{3}}+{{\gamma }_{d}}\text{cos}\left(\omega t \right)+n\left(t \right)\right). $ | (2) |
式中:γd为混沌临界阈值;n(t)为高斯白噪声。
理论上,高斯白噪声输入到处于混沌临界状态的混沌系统中,系统仍保持混沌状态不变,即系统对应的最大Lyapunov指数应保持为正数。但仿真实验中发现在不同精度的临界阈值下输入一定功率的白噪声也会引起系统的状态变化,即系统对应的最大Lyapunov指数可能会变为负数。
以输入噪声功率为10-6为例,分别取γd=0.82,0.825,0.825 8,0.825 843 00,每个临界阈值下进行100次仿真实验,得到噪声功率为10-6时,各仿真中系统对应的最大Lyapunov指数如图 2所示。

|
图 2 在不同精度临界阈值下,系统输入功率为10–6的高斯白噪声后,系统对应的最大Lyapunov指数 Fig. 2 Maximal Lyapunov exponent of chaotic system after inputting gauss noise with power 10–6 into the system under different precision critical value |
定义输入噪声时,系统的虚警率为:
| $ \text{虚警率}=\frac{\text{(}\text{系统最大Lyapunov指数}<\text{0)}\text{的次数}}{\text{仿真实验次数}}\text{.} $ | (3) |
由图 2可知,γd=0.82,0.825,0.825 8,0.825 843 00时,对应的虚警率分别为0%,0%,7%,62%。随着混沌临界阈值的不断精确,系统对噪声越来越敏感,其虚警率增加,原因如下:
1)噪声的频带很宽,其包含外力驱动力频率的窄带可能导致系统由混沌临界状态跳变到大尺度周期状态;
2)随着临界阈值的不断精确,系统越来越接近周期状态,其有序度增加,噪声加入到系统中无法改变其有序度,从而使系统进入到大尺度周期状态。
3.2 输入含噪信号时对检测性能的影响在式(1)的duffing系统处于临界状态时,加入含噪信号,其变为:
| $ \ddot{x}=-k\omega \dot{x}+{{\omega }^{2}}\left(x-{{x}^{3}}+{{\gamma }_{d}}\text{cos}\left(\omega t \right)+a\text{cos}\left(\omega t \right)+n\left(t \right)\right)\text{, } $ | (4) |
式中:γd和n(t)与式(2)的意义相同;a为待测信号幅度。
理论上,含噪信号输入到处于混沌临界状态的混沌系统中,系统应从混沌状态迅速转化为大尺度周期状态,即系统对应的最大Lyapunov指数变为负数。但仿真实验中发现在不同精度的临界阈值下输入一定信噪比的含噪信号也可能不会引起系统的状态变化,即系统对应的最大Lyapunov指数仍保持为正数。
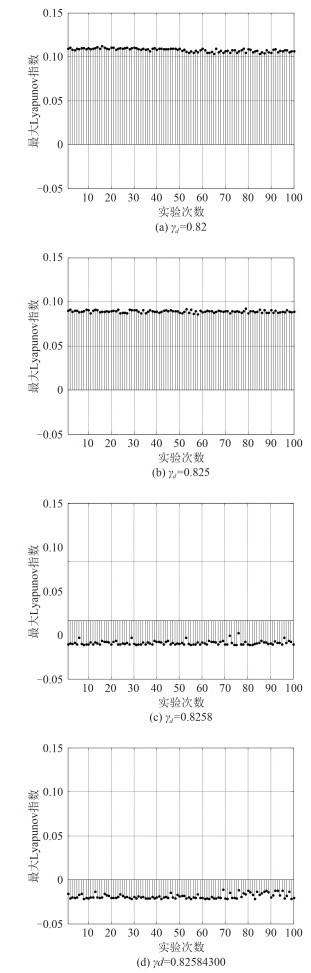
以输入噪声为10-6,输入信号的信噪比为-10 dB为例,分别取γd=0.82,0.825,0.825 8,0.825 843 00,每个临界阈值下进行100次仿真实验,得到噪声功率为10-6,信噪比为-10 dB时,各仿真中系统对应的最大Lyapunov指数如图 3所示。
|
图 3 在不同精度临界阈值下,系统输入信噪比为–10 dB,噪声功率为10–6的含噪信号后,系统对应的最大Lyapunov指数 Fig. 3 Maximal Lyapunov exponent of chaotic system after inputting signal with SNR –10 dB and noise with power 10–6 into the system under different precision critical value |
其中信噪比的定义为:
| $ SNR=10\lg \frac{{{a}^{2}}}{2\times(\text{噪声功率})}\text{, } $ | (5) |
定义输入含噪信号时,系统的检测率为:
| $ \text{检测率}=\frac{\text{(}\text{系统最大}Lyapunov\text{指数}<\text{0)}\text{的次数}}{\text{仿真实验次数}}\text{.} $ | (6) |
由图 3可得,γd=0.82,0.825,0.825 8,0.825 843 00时,对应的检测率分别为0%,0%,100%,100%。可见,随着临界阈值的不断精确,系统对信号的灵敏度增加,这主要是因为随着临界阈值的不断精确,系统越来越接近周期状态,其有序度增加,微小的信号加入到系统中就可以引起系统状态的改变。
3.3 不同情况下的检测性能取噪声功率分别为10-6,10-4和10-2,信噪比分别为-10 dB,-20 dB,-30 dB,-35 dB和-40 dB,得到的总检测结果如表 3所示。
|
|
表 3 混沌系统在不同情况下的检测性能 Tab.3 Detection performance of chaotic system under different cases |
从表可见,不同精度的临界值将影响混沌系统的检测结果,当选取的临界值精度越高时,其能检测到信号的信噪比越低,但其虚警率也越高,因此实际检测时需根据检测的要求来选取合适精度的临界阈值。从表中还可看到噪声强度对混沌系统检测性能也会产生影响,这将在下一阶段中详细研究。
4 结语在混沌系统微弱信号检测中,一般利用Lyapunov指数定性确定混沌系统中由混沌态转化为大尺度周期态的临界阈值,而选取具有不同精度的临界阈值将影响系统的检测性能,临界阈值的精度越高,能够检测到的信噪比越低,但同时虚警率也越高,因此实际检测中需根据对检测性能的要求选取合适精度的临界阈值进行信号检测。
| [1] | 聂春燕. 混沌系统与弱信号检测[M]. 北京: 清华大学出版社, 2009 . |
| [2] | ZHANG M, LIU Z Z, CAO Y, et al. Research and simulation on weak signal detection based on duffing oscillator and damping ratio perturbation[J]. Journal of Measurement Science and Instrumentation , 2011, 2 (2) :161–163. |
| [3] |
张刚, 胡韬, 王颖. 基于Melnikov函数Duffing系统微弱信号检测[J]. 电子测量技术 , 2015, 38 (1) :109–112.
ZHANG Gang, HU Tao, WANG Ying. The weak signal detection based on Duffing system and Melnikov function[J]. Electronic Measurement Technology , 2015, 38 (1) :109–112. |
| [4] |
陈军. 基于混沌理论的检测系统应用研究综述[J]. 甘肃高师学报 , 2013, 18 (2) :21–25.
CHEN Jun. Application research and discussing of detective systems based on chaos theory[J]. Journal of Gansu Normal Colleges , 2013, 18 (2) :21–25. |
| [5] |
陈新国, 王洁芸. 混沌振子在不同初值下检测弱信号的性能分析[J]. 仪器仪表学报 , 2012, 33 (12) :2857–2862.
CHEN Xin-guo, WANG Jie-yun. Performance analysis of weak signal detection based on chaotic oscillator under different initial condition[J]. Chinese Journal of Scientific Instrument , 2012, 33 (12) :2857–2862. |
| [6] |
朱斌. 基于混沌理论的微弱信号检测[J]. 电子科技 , 2010, 23 (2) :65–67.
ZHU Bin. Weak signal detection based on the chaos theory[J]. Electronic Science & Technology , 2010, 23 (2) :65–67. |
| [7] |
石敏, 徐袭. 基于混沌系统的水下目标辐射噪声线谱检测[J]. 舰船科学技术 , 2013, 35 (5) :30–33.
SHI Min, XU Xi. Detection of underwater target radiated noise line-spectra based on chaos system[J]. Ship Science and Technology , 2013, 35 (5) :30–33. |
| [8] |
朱来普, 张陆勇, 谢文凤, 等. 基于Duffing混沌振子的微弱信号检测研究[J]. 无线电工程 , 2012, 42 (1) :17–20.
ZHU Lai-pu, ZHANG Lu-yong, XIE Wen-feng, et al. Research of weak signal detection based on Duffing chaotic oscillator[J]. Radio Engineering , 2012, 42 (1) :17–20. |
| [9] |
李琳, 刘春刚, 石硕, 等. 基于混沌振子和Lyapunov指数的微弱信号检测方法[J]. 黑龙江大学自然科学学报 , 2012, 29 (4) :556–560.
LI Lin, LIU Chun-gang, SHI Shuo, et al. A method of weak signal detection based on chaotic oscillator and Lyapunov exponent[J]. Journal of Natural Science of Heilongjiang University , 2012, 29 (4) :556–560. |
| [10] |
冉莉, 王民. 一种强噪声背景下微弱信号检测方法研究[J]. 信息技术 , 2012 (2) :41–45.
RAN Li, WANG Min. Research on weak signal detection method under the strong noise background[J]. Information Technology , 2012 (2) :41–45. |
| [11] | JIN T, ZHANG H. Statistical approach to weak signal detection and estimation using Duffing chaotic oscillators[J]. Science China Information Sciences , 2011, 54 (11) :2324–2337. DOI:10.1007/s11432-011-4308-6 |
| [12] | 张宾. Lyapunov特性指数的算法研究及其在弱信号混沌检测中的应用[D].长春:吉林大学, 2004. http://cdmd.cnki.com.cn/article/cdmd-10183-2004101756.htm |
 2016, Vol. 38
2016, Vol. 38
