2. 海军大连舰艇学院 军事海洋系, 辽宁 大连 116018
2. Department of Military Oceanography, Dalian Navy Academy, Dalian, 116018, China
岸基声呐布设海域的周边环境复杂,各种海面目标多、干扰强度大、干扰覆盖范围大,严重影响对水下弱目标的远程预警探测,研究如何经过处理得到具有更高信干比与信噪比的信号,从而提高对微弱目标的检测能力显得尤为重要。
空域矩阵滤波技术是一种典型的干扰抑制方法,它是借鉴数字滤波器的概念所引出的,由美国罗德岛大学的Richard Vaccaro等于1994年提出,并于1996年提出了一种优化的方位域矩阵滤波器设计方法[1],这些研究只针对空间某一方位范围空域滤波,通过对感兴趣的空间设定通带或阻带来实现干扰抑制。此类方法能够有效地抑制或滤除干扰,但研究的声源频率为单频率或离散多频率点而非一般意义上的宽带源,而且设计矩阵滤波器时的声源频率点及水声环境参数已知。尽管仿真研究取得了比较好的效果,但以上条件在实际应用中难以具备。
另一种重要的干扰抑制方法是子空间类干扰抑制方法,它主要通过对接收阵列数据的协方差矩阵进行特征分析,根据特征值的大小和特征向量的方向信息剔除接收数据中代表干扰及噪声信息的特征向量,达到提高信干比、信噪比的目的。Cox[2]于2000年提出了一种子空间的自适应干扰抑制方法,该方法主要针对强干扰环境下微弱目标的检测,根据干扰能量远大于目标信号能量的先验知识,将较大的特征值对应的特征向量归属于干扰子空间,通过去除该特征值对应的特征向量从而达到抑制强干扰的目的。
本文方法主要思想是基于子空间的干扰抑制,通过对接收数据协方差矩阵进行特征分析,将每一个特征值及其对应的特征向量重构成子矩阵,然后进行常规波束形成[3-4](CBF),分离出CBF功率谱估计谱峰在预估方位范围内的子矩阵进行累加,得到抑制了干扰及噪声的新协方差矩阵,以此来消除干扰的影响。本文通过理论分析与数值仿真对本文方法的可行性和有效性进行验证。
1 数据模型根据空间谱估计理论[5],假设一个阵元数M、相邻阵元间距为d的水平均匀线列阵,D个与噪声不相关的信源从
| $ X\left({{f}_{l}} \right)=A\left({{f}_{l}} \right)S\left({{f}_{l}} \right)+N\left({{f}_{l}} \right)\text{, } $ | (1) |
式中:S(fl)为信源数据矢量的频域;N(fl)为加性高斯白噪声的频域;
| $ a\left({{f}_{l}}, {{\theta }_{i}} \right)=[1, {{e}^{-j2\pi {{f}_{l}}d\sin {{\theta }_{i}}/c}}, \cdots, {{e}^{-j2\pi {{f}_{l}}\left(M-1 \right)d\sin {{\theta }_{i}}/c}}]\text{, } $ | (2) |
式中:c为声速。
阵列接收数据的协方差矩阵可表示为
| $ \boldsymbol{R}\left({{f}_{l}} \right)=E\left\{ X\left({{f}_{l}} \right){{X}^{H}}\left({{f}_{l}} \right)\right\}={{\boldsymbol{R}}_{s}}\left({{f}_{l}} \right)+{{\boldsymbol{R}}_{n}}\left({{f}_{l}} \right)\text{.} $ | (3) |
式中:R s(fl)表示频率为fl的信源数据协方差矩阵;R n(fl)表示频率为fl的噪声分量协方差矩阵;上标H为共轭转置。
2 基于协方差矩阵子矩阵的干扰抑制方法根据上述阵列数据模型,常规波束形成(CBF)的空间功率谱估计可表示为:
| $ B\left({{f}_{l}}, \theta \right)={{\omega }^{H}}\left({{f}_{l}}, \theta \right)R\left({{f}_{l}} \right)\omega \left({{f}_{l}}, \theta \right)\text{, } $ | (4) |
其中,
| $ {{\omega }^{H}}\left({{f}_{l}}, \theta \right)=\left[1, {{e}^{-j2\pi {{f}_{l}}d\sin \theta/c}}, \cdots, {{e}^{-j2\pi {{f}_{l}}\left(M-1 \right)d\sin \theta/c}} \right]\text{.} $ | (5) |
式中:θ为目标相对于水平线阵的空间角度,$\theta \in \left[0{}^\circ, 180{}^\circ \right]$。频间非相干处理的宽带CBF空间功率谱估计可以表示为:
| $ B\left(\theta \right)=\sum\limits_{l=1}^{L}{B\left({{f}_{l}}, \theta \right)}\text{, } $ | (6) |
其中L为处理的频点数。
根据特征分解理论[6],协方差矩阵可以用其特征值和特征向量表示成以下形式:
| $ R\left({{f}_{l}} \right)=E\Lambda {{E}^{H}}=\sum\limits_{i=1}^{M}{{{\lambda }_{i}}\left({{f}_{l}} \right){{v}_{i}}\left({{f}_{l}} \right){{v}_{i}}{{\left({{f}_{l}} \right)}^{H}}}\text{.} $ | (7) |
式中:λi(fl)和vi(fl)分别为R(fl)的第i个特征值以及对应的特征向量;Λ和E分别为相应的特征值矩阵以及特征向量矩阵。则R(fl)第i个特征值及其对应的特征向量构成的子矩阵可以表示为:
| $ {{\boldsymbol{R}}_{i}}\left({{f}_{l}} \right)={{\lambda }_{i}}\left({{f}_{l}} \right){{v}_{i}}\left({{f}_{l}} \right){{v}_{i}}{{\left({{f}_{l}} \right)}^{H}}, $ | (8) |
并且其子矩阵满足:
| $ \boldsymbol{R}\left({{f}_{l}} \right)=\sum\limits_{i=1}^{M}{{{R}_{i}}\left({{f}_{l}} \right)}\text{, } $ | (9) |
则阵列接收数据的CBF空间功率谱估计为:
| $ \begin{align} &B\left({{f}_{l}}, \theta \right)={{\omega }^{H}}\left({{f}_{l}}, \theta \right)\sum\limits_{i=1}^{M}{{{R}_{i}}\left({{f}_{l}} \right)}\omega \left({{f}_{l}}, \theta \right)=\\ &\sum\limits_{i=1}^{M}{{{\omega }^{H}}\left({{f}_{l}}, \theta \right){{R}_{i}}\left({{f}_{l}} \right)\omega \left({{f}_{l}}, \theta \right)}\text{, } \\ \end{align} $ | (10) |
由式(10)可知,在一个频点上,
| $ {{B}_{i}}\left({{f}_{l}}, \theta \right)={{\omega }^{H}}\left({{f}_{l}}, \theta \right){{R}_{i}}\left({{f}_{l}} \right)\omega \left({{f}_{l}}, \theta \right)\text{.} $ | (11) |
如果
在实际应用中,往往无法预先知道目标的真实方位,但可以通过其他一些方法手段得到关于目标方位范围的先验信息,假定目标方位的范围区间为
| $ {{\theta }_{Di}}=\arg \max \left({{B}_{i}}\left({{f}_{l}}, \theta \right)\right)\text{.} $ | (12) |
式中:
| $ \bar{R}\left({{f}_{l}} \right)=\sum{{{R}_{i}}\left({{f}_{l}} \right)}, \ {{\theta }_{T1}}\le {{\theta }_{Di}}\le {{\theta }_{T2}}\text{, } $ | (13) |
即可得到抑制了目标范围之外干扰的CBF空间功率谱估计为:
| $ \bar{B}\left({{f}_{l}}, \theta \right)={{\omega }^{H}}\left({{f}_{l}}, \theta \right)\bar{R}\left({{f}_{l}} \right)\omega \left({{f}_{l}}, \theta \right)\text{, } $ | (14) |
频间非相干处理的宽带CBF空间功率谱估计为:
| $ \bar{B}\left(\theta \right)=\frac{1}{L}\sum\limits_{l=1}^{L}{\bar{B}\left({{f}_{l}}, \theta \right)}\text{.} $ | (15) |
在相干环境下,信号子空间和噪声子空间不再满足正交性,在使用本文方法前采用前后向平滑算法[7]来实现相干信号的解相干。空间平滑算法的主要思想是把M个阵元的阵列分成相互重叠的几个子阵列,对子阵的相关矩阵求和加权平均,使求和后的信源协方差矩阵的秩等于信源数,从而达到解相干的目的。
取子阵的阵元数为m,则子阵数为L=M − m+1,取m, L > D。则前后向空间平滑算法的公式表示为:
| $ \bar{\bar{R}}\left({{f}_{l}} \right)=\frac{1}{L}\sum\limits_{k=1}^{L}{{{F}_{k}}\cdot \left(\boldsymbol{R}\left({{f}_{l}} \right)+\boldsymbol{J}\boldsymbol{\cdot }{{\boldsymbol{R}}^{*}}\left({{f}_{l}} \right)\cdot J \right)\cdot F_{k}^{\text{T}}}\text{.} $ | (16) |
式中:
将上式得到的
本节通过数值仿真来分析本文方法的有效性。仿真过程中假设接收阵列为48阵元、相邻阵元间距为5 m的均匀线列阵,频间非相干处理的频率为50~150 Hz,共101个频点,采样频率为2 000 Hz,声速1 500 m/s。假设阵元噪声为宽带高斯白噪声,信源采用宽带白噪声形式,接收阵元信噪比为-5 dB。仿真处理中,FFT样本数为2 000,频域采样次数为20次,样本时长为20 s。
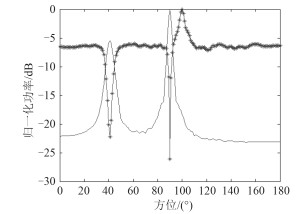
4.1 信源非相干假设存在3个互不相干的信源,其中目标信号方位为100°,2个干扰的方向分别为90°和40°,信干比分别为-25 dB和-20 dB,取预估目标方向位于95°~105°的范围内,干扰抑制前后的CBF归一化功率谱估计结果对比如图 1所示。
|
图 1 干扰抑制前后CBF归一化空间功率谱估计结果对比 Fig. 1 Comparison of CBF normalized spatial power spectrum estimation results before and after interference suppression |
从图 1可看出,在干扰与目标方位角度比较接近,而且信干比较大时,CBF方向估计中的目标已经完全被邻近的强干扰掩盖,而本文提出的方法可以有效抑制干扰,提高了输出信干比,准确地检测出目标的真实方位。
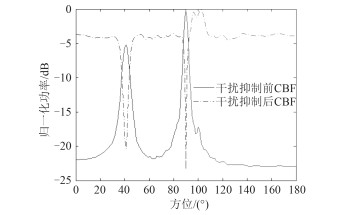
4.2 信源相干本文提出的方法主要对协方差矩阵进行特征分析,属于子空间类方法,当信源之间相关时,尤其在干扰与目标相关时,相关性越强,性能下降越明显。仿真过程中,取3个信源,其中90°方向干扰与100°方向目标完全相干且信干比为-25 dB,40°方向干扰与其他2个信源都不相关且信干比为-20 dB,目标预估方位95°~105°,仿真结果如图 2所示。
|
图 2 100°信源与90°信源相干时干扰抑制前后CBF归一化空间功率谱估计结果对比 Fig. 2 Comparison of CBF normalized spatial power spectrum estimation results before and after interference suppression between source at 100° and source at 90° |
从图 2可看出,在目标方向信源与邻近干扰信源完全相干时,本文方法仍然能抑制干扰,但是无法检测出真实目标方位,并且由于目标与干扰的相干,信号协方差矩阵不满秩,在抑制干扰的同时也抑制了目标信号,输出信噪比与信干比都较低。
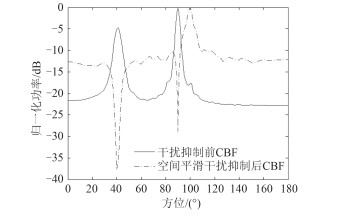
针对上述目标与干扰相干时输出信噪比和信干比较低的问题,在这里采用前后向空间平滑算法进行去相干,然后再通过本文方法进行干扰抑制。其他仿真条件不变,采用第3节所述的前后向空间平滑算法,取36阵元的子阵列进行空间平滑,仿真结果如图 3所示。
|
图 3 空间平滑前后干扰抑制后CBF归一化功率谱估计结果对比 Fig. 3 Comparison of CBF normalized power spectrum estimation results before and after spatial smoothing |
从图 3仿真结果可看出,在相干环境下,通过前后向空间平滑之后,极大地提高了输出信干比、信噪比,具有较好的干扰抑制效果。
4.3 影响该方法性能的因素通过仿真实验的对比,分析该方法在不同信噪比、不同信干比、不同预估方位范围设定时的性能。仿真过程假设3个非相干信源,目标信号方向100°,干扰方向为90°和40°。
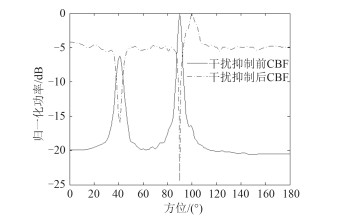
首先分析信噪比对该方法的影响,对比接收阵元信噪比在-8 dB与-5 dB时的性能,如图 4所示。
|
图 4 信噪比为–8 dB,预估范围为95°~105°时的干扰抑制前后CBF归一化功率谱估计结果 Fig. 4 Signal to noise ratio of –8 dB, interference suppression before and after the CBF normalized power spectrum estimation results at estimated range of 95°~105° |
对比图 4与图 1的仿真结果,并且经过多次仿真试验发现,信噪比越低,该方法对感兴趣目标的检测概率越低,干扰抑制效果也有所降低。
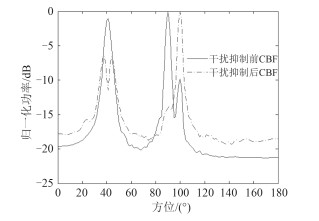
分析不同信干比对该方法的影响。设定90°和40°方向干扰的信干比都为-10 dB,利用该方法进行仿真得到结果如图 5所示。
对比图 5与图 1的仿真结果,发现该方法在信干比较高时,虽然能够检测出目标信号,但是干扰抑制效果不明显,多次仿真实验发现,干扰强度大于信号强度的前提下,信干比越高,干扰抑制效果越差,这是由于目标信号与干扰能量接近时,在各个特征向量占主导的信号区分不够明显,但是该方法仍然能够检测出目标信号。
|
图 5 90°和40°方向干扰的信干比都为–10 dB,预估方位范围为95°~105°时的干扰抑制前后CBF归一化功率谱估计结果 Fig. 5 SIR is –10dB, interference suppression before and after the CBF normalized power spectrum estimation results at estimated azimuth range of 95°~105° |
最后对比不同预估范围的设定对该方法的影响,设定预估范围为91°~109°与90°~110°,其他仿真条件与图 1一样时,仿真结果如图 6所示。
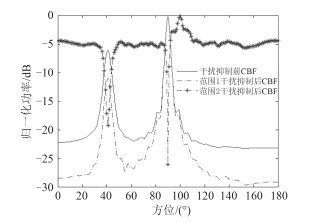
|
图 6 预估范围不同时干扰抑制前后CBF归一化功率谱估计结果对比,范围1代表 90°~110°,范围2代表 91°~109° Fig. 6 Comparison of CBF normalized spatial power spectrum estimation results before and after interference suppression under different estimated range, range 1 is 90°~110°, range 2 is 91°~109° |
对比图 6与图 1的结果发现,目标预估范围在90°~110°时,此时预估范围内包含了目标邻近的强干扰,导致该方法失效,不能抑制干扰,也不能检测出目标信号,而经过多次仿真试验,目标预估范围越精确,干扰抑制效果越好,输出信噪比和信干比越高。
5 结语本文提出了一种基于协方差矩阵的干扰抑制方法,假设目标方位的范围已知,通过对接收数据协方差矩阵进行特征分解,得到代表特征值及其相应特征向量的子矩阵,对所有子矩阵进行谱峰搜索,得到谱峰在预估目标方位的子矩阵然后进行累加,得到抑制了干扰的协方差矩阵,提高了输出信干比和处理增益。数值仿真表明,该方法可以有效抑制不在预估方向范围的干扰,为目标进一步的识别与跟踪创造了有利条件。
本文方法的先验信息是目标方位的预估范围,当预估范围不够精确,其中包含有干扰时该方法失效,无法抑制范围内的干扰。在后续研究中,针对在预估范围内的干扰强度较大时,无法检测出微弱目标信号的问题,准备在本方法的基础上,依据干扰强度远大于目标信号的前提,通过剔除大的特征值来抑制预估方向范围内的强干扰,或是通过水面水下的起伏特性差异[8]来抑制水面干扰、检测水下目标,进一步提高干扰抑制能力。
| [1] | VACCARO R J, HARRISON B F. Optimal matrix-filter design[J]. IEEE Transactions on Signal Processing , 1996, 44 (3) :705–709. DOI:10.1109/78.489044 |
| [2] | COX H. Multi-rate adaptive beamforming (MRABF)[C]//Proceedings of the 2000 IEEE sensor array and multichannel signal processing workshop. Cambridge MA:IEEE, 2000:306-309. |
| [3] | 孙超. 水下多传感器阵列信号处理[M]. 西安: 西北工业大学出版社, 2007 : 230 -277. |
| [4] | CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE , 1969, 57 (8) :1408–1418. DOI:10.1109/PROC.1969.7278 |
| [5] | 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004 : 18 -81. |
| [6] | 张贤达. 矩阵分析与应用法[M]. 北京: 清华大学出版社, 2004 : 64 -71. |
| [7] | PILLAI S U, KWON B H. Forward/backward spatial smoothing techniques for the coherent signal identification[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing , 1989, 37 (1) :8–15. DOI:10.1109/29.17496 |
| [8] | WAGSTAFF R A. Advanced signal processing filter:US 6036351[P]. 2000-03-14. |
 2016, Vol. 38
2016, Vol. 38
