舰船作直航向航行时,由于受风浪、流、舰船摇摆等干扰造成电罗经航向幅值摆动,出现电罗经航向不稳的现象,在一定程度上影响了利用电罗经航向值观测目标的精度。因此,研究电罗经航向输出值摆动变化规律,提高电罗经航向值的可靠性具有重要的实用价值。小波分析以其时频多分辨分析的优良特性特别适宜于分析和处理非平稳信号,利用小波分析具有很好的消噪效果特性[1],通过对获得的原始数据进行小波变换可以得到滤除噪声后的有用信号。傅里叶变换(Fourier transformation)是一种时-频域转化的分析方法,能够提取时域信号的频率特征[2]。四参数估计法是一种基本的信号处理方法,在很多场合下得到应用,如评价数据采集系统的有效位数、采集速率、交流增益、通道间延迟、触发特性等。文献[3]指出,多数四参数正弦波拟合算法的共同缺点是拟合过程需要大量迭代运算时间,从而影响了算法的效率和实时性应用。
本文通过对电罗经实测数据采用小波消噪后的数据进行傅里叶分析,确定能量频点,既可避免迭代运算过程,又可通过不断获得的新信息,采用自适应四参数估计法对电罗经直航向模型进行实时地自适应高精度估计预测。文中提出的方法为估计电罗经航向提供了一种思路。
1 小波变换小波变换作为一种时频分析工具,它具有时间域和频率域的良好局部化性质。所谓小波是指由基本小波
| $ {{\psi }_{a, b}}(t)=\frac{1}{\sqrt{a}}\psi(\frac{t-b}{a}), $ | (1) |
式中:a为尺度参数,它改变滤波器的频带宽度;b为位置信息,它决定小波变换的空域和时域信息。
则待分析信号s(t)的小波变换为[4]:
| $ W{{T}_{s}}(a, b)=\frac{1}{\sqrt{a}}\int_{-\infty }^{\infty }{s(t)\psi(\frac{t-b}{a})\operatorname{d}t}\triangleq \left\langle s(t), {{\psi }_{a, b}}(t)\right\rangle \text{.} $ | (2) |
式中:s(t)为时间信号;t为时间。
通过适当选择参数a、b值,使得小波变换在时频平面上形成一种合适的网格,即可以形成多分辨率的窗口。
小波用于消噪和函数逼近是Donobo等的研究[3],本文采用db5小波对电罗经直航向数据进行5层分解。选取稳定航向H=222°的1组实测数据进行分析,结果如图 1所示。

|
图 1 小波分析 Fig. 1 Wavelet transform |
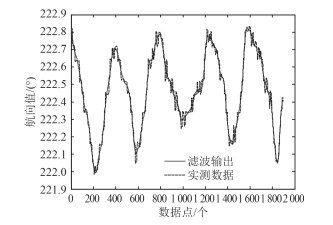
经过小波重构后的电罗经信号和原始信号相比变得更加平滑,有效抑制了高频扰动,如图 2所示。
|
图 2 小波滤波信号 Fig. 2 Signal of wavelet filter |
对于信号的分析既可以在时域中进行,也可以在频域中进行。傅里叶变换是将信号从时域变换到频域,在信号分析中占有极其重要的地位。
一维离散傅里叶变换的定义:如果有一个向量x(n),其离散傅里叶变换结果为x(k),x(k)与x(n)的关系如下[5-6]:
| $ \left\{ \begin{array}{*{35}{l}} x(k)=DFS[x(n)]=\sum\limits_{n=1}^{N}{x(n){{e}^{-j2\pi(k-1)\frac{n-1}{N}}}}, 1\le k\le N\text{, } \\ x(n)=IDFS[x(k)]=\frac{1}{N}\sum\limits_{k=1}^{N}{}x(k){{e}^{j2\pi(k-1)\frac{n-1}{N}}}, 1\le n\le N\text{.} \\ \end{array} \right. $ | (3) |
式中:N为向量x(n)的长度;DFS为离散傅里叶级数的正变换;IDFS为离散傅里叶级数的逆变换。
本文通过傅里叶变换提取直航向信号的频谱特性。取样频率fs与取样周期T的关系为fs=1/T[7],设序列的周期为NT,则对频谱取样的谱间距为1/NT。
首先,提取第1个周期T1的频谱特性,频谱间隔为1/T1;其次,提取第2个周期T2的频谱特性,频谱间隔为1/T2。
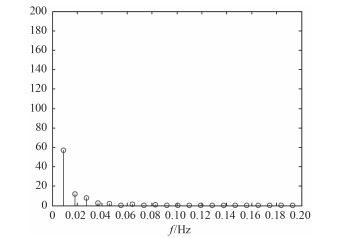
由图 3和图 4可知,通过傅里叶变换可以方便快捷地提取原始信号的频谱特性,通过图可以有效提取信号的基波和谐波分量。

|
图 3 T1频率特征 Fig. 3 frequency characteristics of T1 |
|
图 4 T2 频率特征 Fig. 4 frequency characteristics of T2 |
设被采样的正弦信号为:
| $ S(t)=A\sin(wt+\theta)+C, $ | (4) |
式中:A为信号幅度;w为信号频率;θ为信号相位;C为信号的常值偏移。
对于任意正弦信号的表示均可通过采用A,w,θ,C四个参数加以实现,这4个参数称为正弦信号的四参数[8-10]。也可以用另外4个参数来表示:
| $ S(t)={{A}_{0}}\cos({{w}_{0}}t)+{{B}_{0}}\sin({{w}_{0}}t)+{{C}_{0}}\text{.} $ | (5) |
式中:
式中余弦幅度A0,B0,C0,w0也称为正弦信号四参数,与式(4)中的幅度、频率、相位、常值偏移在描述正弦信号特征时等价。
3.2 估计正弦信号三参数的算法设式(5)正弦信号在tk时刻(k=0,1,2…)的采样值为y(k),正弦幅度、余弦幅度和常值偏移3个参数估计值分别为A,B,C,则估计值与真实值之间的误差平方和为:
| $ E(A, B, C)=\sum\limits_{k=0}^{N-1}{}{{[y(k)-A\cos({{w}_{0}}t)-B\sin({{w}_{0}}t)-C]}^{2}}\text{, } $ | (6) |
式中N为采样长度。
令
| $ \begin{align} &\boldsymbol{D}=\left[\begin{matrix} \cos({{w}_{0}}{{t}_{0}})&\sin({{w}_{0}}{{t}_{0}})&1 \\ \cos({{w}_{0}}{{t}_{1}})&\sin({{w}_{0}}{{t}_{1}})&1 \\ \vdots &\vdots &\vdots \\ \cos({{w}_{0}}{{t}_{N-1}})&\sin({{w}_{0}}{{t}_{N-1}})&1 \\ \end{matrix} \right]\text{, } \\ &\boldsymbol{Y}=\left[\begin{matrix} y(0)\\ y(1)\\ \vdots \\ y(N-1)\\ \end{matrix} \right], X=\left[\begin{matrix} A \\ B \\ C \\ \end{matrix} \right]\text{.} \\ \end{align} $ |
则式(6)所描述的正弦信号中三参数的最小二乘解为[10]:
| $ X={{({{\boldsymbol{D}}^{\text{T}}}\boldsymbol{D})}^{-1}}({{\boldsymbol{D}}^{\text{T}}}Y)\text{.} $ | (7) |
由上可知,三参数估计法就是在获得信号频率并且使式(6)中所述参差的误差平方和最小的最小二乘估计方法。四参数估计法在未知信号频率的情况下,需要进行大量的迭代计算,且计算结果并不一定收敛,因此考虑采用傅里叶变换获得高精度的频率值,这就避免了繁琐的迭代过程,并将其应用与四参数估计过程,利用上述的最小二乘估计方法求得精确的模型参数。
3.3 傅里叶展开法建模由图 2可知,电罗经直航向信号由于受到一系列外扰及舰船本身摇摆的影响,呈现出较强的周期性摆动。由于无法用简单的周期模型进行描述,考虑采用傅里叶级数展开法进行航向建模。令直航向模型为H=f(t),其中H为航向,t为时间。通过傅里叶变换可成功提取基波和各次谐波。
由狄利克雷收敛定理可知,上述提出的模型应满足一定的条件,即设f(t)是周期为T的周期函数,如果它满足:1)在一个周期内连续或只有有限个第1类间断点,2)在1个周期内至多只有有限个极值点,则f(t)的傅里叶级数收敛,并且当t为f(t)连续点时,级数收敛f(t)。
由于实测数据周期性较强,且在1个周期内连续,现将H=f(t)傅里叶级数展开为:
| $ H=f(t)=\sum\limits_{i=1}^{n}{[{{A}_{i}}\sin({{w}_{i}}t+{{\theta }_{i}})+{{C}_{i}}]}\text{, } $ | (8) |
式中:n为整数,也是频点数;Ai,wi,θi,Ci为待估参数。
可将式(8)写为如下形式:
| $ H=f(t)=\sum\limits_{i=1}^{n}{[{{A}_{i}}\sin({{w}_{i}}t)+{{B}_{i}}\sin({{w}_{i}}t)+{{C}_{i}}]}\text{.} $ | (9) |
式中各参数定义同式(5)。
采用四参数法的具体估计步骤如下:
1)令i=1,确定估计信号频率的大致区间,首先考虑第1个周期T1,由傅里叶变换可以得到基波和谐波分量。由图 3可知,能量越大对信号的影响越大,因此选取基波在内的前5个频点。
2)令基波信号频率为w01,其余四点谐波频率分别为w02,w03,w04,w05,5个频点间隔为
3)令
4)比较步骤3)中的2M+1个误差平方和,选取误差平方和最小的Aij,Bij,C1j,w1j,而为四参数的第1次估计值,其中频率最大估计偏差
5)i=i+1,
6)令新区间为[wi,wh],等间距的取2M+1个点,重复步骤3和步骤4,计算出对应的参数估计值和误差平方和。令其为第i次估计值。
7)重复步骤3和步骤4,直到找到满足精度要求的信号频率,同时估计出其他3个参数,则最终的A,B,C和w为四参数的高精度估计值。其中,频率估计的最大误差为
8)以上步骤为第1周期的参数估计,在获得了高精度的模型后,可以有效地对第2个周期航向数据进行实时地预测,同时当获得第2周期实测数据后,又可以对模型参数进行更新修正,即不断利用新信息计算新时刻的模型,从而满足对第2周期中下一时刻的高精度预测要求。
由以上所述步骤可知,在每个周期中重复步骤1~步骤7就可以获得高精度的自适应电罗经航向模型,同时可以人为的增大迭代次数i来提高精度。
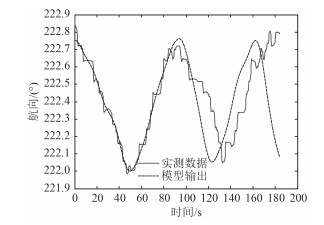
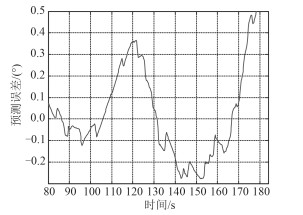
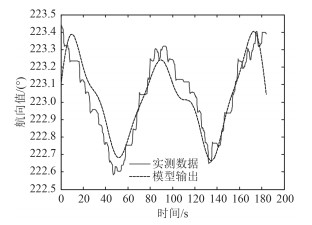
4 模型验证本文采用第1节所选择的实测数据进行验证,首先通过小波变换进行高频消噪处理,获得较为平稳的航向信号,采用傅里叶变换将航向的时域信号转化为频域信号进行分析,确定能量较高的前5个频点,对第1个周期进行建模,同时对第2个周期进行自适应预测,即在不断获得第2周期实测数据的基础上不断对下一时间点作有效预测,图 5和图 6为未加自适应修正的模型输出及预测结果,图 7和图 8为加入自适应修正的四参数估计法迭代模型输出及预测结果。
|
图 5 估计模型与预测 Fig. 5 estimation model and prediction |
|
图 6 预测误差 Fig. 6 prediction error |
|
图 7 自适应估计模型与预测 Fig. 7 Self-adaptive estimation model and prediction |

|
图 8 自适应预测误差 Fig. 8 Self-adaptive prediction error |
由图 5~图 8所示,基于正弦信号四参数估计法的自适应估计算法能够满足预测精度要求,且具有实时性,利用不断获得的新信息采取在线修正模型参数的方法,使其能够比较真实的描述和预测电罗经直航向输出,在预测效果上明显优于传统的四参数估计法。
5 结语通过小波滤波,使得电罗经直航向信号变得平稳,有效滤除高频干扰,为对信号进行傅里叶分析打下良好基础,通过时频转换的傅里叶分析法,可以确定信号中能量较大的频点,利用所得频点对航向模型进行傅里叶展开建模,并对模型参数进行在线地自适应迭代估计,结果表明,模型预测效果较好,为下一步修正电罗经误差打下一定的基础。
| [1] |
谢荣生, 孙枫, 郝燕玲, 等. 基于小波分析的船用捷联陀螺信号滤波方法[J]. 哈尔滨工程大学学报 , 2001, 22 (2) :24–26.
XIE Rong-sheng, SUN Feng, HAO Yan-ling, et al. Filtering of ship'sstrap-down gyroscope signals based on wavelet analysis[J]. Journal of Harbin Engineering University , 2001, 22 (2) :24–26. |
| [2] |
刘前林, 王立世, 黄新建. 运用傅里叶变换对差分吸收光谱的解析[J]. 光谱学与光谱分析 , 2008, 28 (5) :1076–1079.
LIU Qian-lin, WANG Li-shi, HUANG Xin-jian. Using fourier transform to analyse differential optical absorption spectrum[J]. Spectroscopy and Spectral Analysis , 2008, 28 (5) :1076–1079. |
| [3] |
梁志国, 张大治, 孙璟宇, 等. 四参数正弦波曲线拟合的快速算法[J]. 计测技术 , 2006, 26 (1) :4–7.
LIANG Zhi-guo, ZHANG Da-zhi, SUN Jing-yu, et al. A fast arithmetic method of four-parameter sine wave curve-fit[J]. Theory and Practice , 2006, 26 (1) :4–7. |
| [4] |
万彦辉, 秦永元. 小波分析在陀螺信号滤波中的研究[J]. 压电与声光 , 2005, 27 (4) :455–457.
WAN Yan-hui, QING Yong-yuan. Application of wavelet analysis in gyro signal filtering[J]. Piezoelectrics and Acoustooptics , 2005, 27 (4) :455–457. |
| [5] |
牟龙华, 邢锦磊. 基于傅里叶变换的精确频率测量算法[J]. 电力系统自动化 , 2008, 32 (23) :67–70.
MOU Long-hua, XING Jin-lei. An accurate frequency measuring algorithm for power systems based on fourier transform[J]. utomation of Electric Power Systems , 2008, 32 (23) :67–70. |
| [6] | BOGGESS A, NARCOWICH F J. A first course in wavelets with fourier analysis [M].2nd ed. Beijing: Publishing House of Electronics Industry, 2010 . |
| [7] | 王世一. 数字信号处理[M].2版. 北京: 北京理工大学出版社, 2011 : 13 -15. |
| [8] | WERNICK M N, MORRIS G M. Effect of spatial coherence on knife-edge measurements of detector modulation transfer function[J]. Applied Ooptics , 1994, 33 (25) :5906–5913. DOI:10.1364/AO.33.005906 |
| [9] | JENQ Y C, CROSBY P B. Sinewave parameter estimation algorithm with application to waveform digitizer effective bits measurement[J]. IEEE Transactions on Instrumentation and Measurement , 1988, 37 (4) :529–532. DOI:10.1109/19.9806 |
| [10] |
吴义华, 杨俊峰, 陈敬原, 等. 正弦信号四参数的高精度估计算法[J]. 中国科学技术大学学报 , 2006, 36 (6) :625–629.
WU Yi-hua, YANG Jun-feng, CHEN Jing-yuan, et al. High accuracy estimation algorithm for 4 parameters of sine-wave[J]. Journal of University of Science and Technology of China , 2006, 36 (6) :625–629. |
 2016, Vol. 38
2016, Vol. 38
