舰船综合电力系统(IPS)是将发电、日常用电、推进供电、高能武器发射供电等综合为一体的舰船电力系统。它将传统舰船相互独立的动力和电力两大系统合而为一,实现了全舰能量的综合利用,代表着未来舰船发展的方向[1]。
目前舰船综合电力系统的建模研究主要集中在发电、储能、推进供电、日常用电这几方面。随着诸如电磁轨道炮、激光炮等高能武器的发展的日趋成熟,其上舰的趋势也愈发明显。这些装舰的脉冲负载由于非周期性、瞬时大功率等特性使得综合电力系统变得更加复杂。因而有必要对含高能脉冲负载的综合电力系统的进行建模仿真来量化评估其对系统性能影响,为未来的工程应用提供的理论支撑。文献[2]中进行了应用飞轮储能系统来加强综合电力系统的稳定性和电能品质的研究。文献[3]考虑了各种因素影响下,建立了一种电磁轨道炮模型,整个模型比较复杂, 并进行了发射实验来进行效率的量化评估, 展望了其应用前景。目前,美国正在进行海试的最新的驱逐舰DDG-1000采用的是全电力推进系统,并且预计于2017年进行电磁轨道炮的舰载测试。为了对含高能脉冲武器负载的综合电力系统进行模拟仿真研究,本文分析电磁轨道炮的动态特性,在Matlab/simulink中建立简化的电磁轨道炮的模型,并进行仿真。将建立的电磁轨道炮模型嵌入至简化的综合电力系统仿真模型中运行仿真,研究高能脉冲武器负载的运行对综合电力系统电能品质的影响。
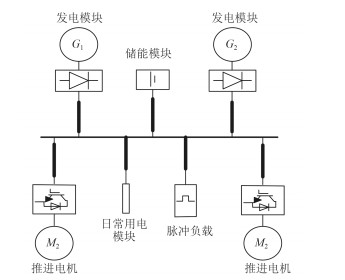
1 综合电力系统拓扑结构本文研究的简化综合电力系统拓扑结构如图 1所示,该系统采用的是中压直流电网供电。发电机G1和G2是带整流系统的发电模块,为全船的日常用电和推进负载及脉冲负载供电;推进模块是由变频器驱动的电动机M1和M2组成,为舰船提供动力;日常用电模块主要是阻感负载;脉冲负载模块是指诸如激光武器、电磁轨道炮等高能脉冲武器负载;储能模块包括飞轮储能、超级电容等储能模块。
|
图 1 简化综合电力系统结构图 Fig. 1 Simplified diagram of integrated power system |
十二相整流发电机系统因具有直流电压脉动小、不受换向限制、可靠性高、维护方便等突出优点,而在舰船电力推进等领域得到广泛应用[4]。在本文所示的简化综合电力系统仿真模型中,以其作为发电模块,并建立相应的仿真模型。在dq0坐标系下,采用理想电机模型,转子交轴上有交轴阻尼绕组(kq)和交轴稳定绕组(fq);直轴上有2套绕组,分别是直轴阻尼绕组(kd)和励磁绕组(fd)。忽略转速变化以及空间谐波磁场,定、转子均采用电动机惯例,可得十二相同步发电机的电压方程、磁链方程如下[4-5]:
| $ \left\{ \begin{array}{l} {{\boldsymbol{u}}_{{{dq0}}}} = {{p}}{{\boldsymbol{\psi }}_{{{dq0}}}} + {\boldsymbol{A}}{{\boldsymbol{\psi }}_{{{dq0}}}}{{p}}\theta + {{\boldsymbol{R}}_{{{dq0}}}}{{\boldsymbol{i}}_{{{dq0}}}}{\rm{ }}{\text{,}}\\ {{\boldsymbol{\psi }}_{{{dq0}}}} = {{\boldsymbol{X}}_{{{dq0}}}}{{\boldsymbol{i}}_{{{dq0}}}}{\text{。}} \end{array} \right. $ | (1) |
式中:ψdq0=[ψd1ψq1ψ01ψd2ψq2ψ02ψd3ψq3ψ03ψd4ψq4ψ04ψfdψkdψfqψkq]T为磁链向量;udq0=[ud1uq1u01ud2uq2u02ud3uq3u03 ud4uq4u04ufd 0 0 0]T为电压向量;idq0=[id1iq1i01id2iq2i02id3iq3 i03id4iq4i04ifd ikdifq ikq]T为电流向量;Rdq0=diag(r r r r r r r r r r r r rfd rkd rfq rkq)为电阻矩阵;A=diag(A11 A22 A33 A44 0)为转换矩阵;0为3 × 3的零矩阵;θ为转子机械角;Xdq0为感抗矩阵,且
| $ {{\boldsymbol{A}}_{ii}}=\left[\begin{matrix} 0 &-1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right], $ |
| $ {\boldsymbol{X}_{dq0}}=\left[\begin{matrix} {\boldsymbol{X}_{11}} & {\boldsymbol{X}_{12}} & {\boldsymbol{X}_{13}} & {\boldsymbol{X}_{14}} & {\boldsymbol{X}_{1r}} \\ {\boldsymbol{X}_{21}} & {\boldsymbol{X}_{22}} & {\boldsymbol{X}_{23}} & {\boldsymbol{X}_{24}} & {\boldsymbol{X}_{{2r}}} \\ {\boldsymbol{X}_{31}} & {\boldsymbol{X}_{32}} & {\boldsymbol{X}_{33}} & {\boldsymbol{X}_{34}} & {\boldsymbol{X}_{{3r}}} \\ {\boldsymbol{X}_{41}} & {\boldsymbol{X}_{42}} & {\boldsymbol{X}_{43}} & {\boldsymbol{X}_{44}} & {\boldsymbol{X}_{{4r}}} \\ {\boldsymbol{X}_{{r}1}} & {\boldsymbol{X}_{{r}2}} & {\boldsymbol{X}_{{r}3}} & {\boldsymbol{X}_{{r}4}} & {\boldsymbol{X}_{{rr}}} \\ \end{matrix} \right], $ |
| $ {\boldsymbol{X}_{ii}}=\left[\begin{matrix} {{x}_{{dy}}} & 0 & 0 \\ 0 & {{x}_{{qy}}} & 0 \\ 0 & 0 & {{x}_{{0y}}} \\ \end{matrix} \right], $ |
| $ {\boldsymbol{X}_{12}}={\boldsymbol{X}_{23}}={\boldsymbol{X}_{34}}={\boldsymbol{X}_{14}}=\left[\begin{matrix} {{x}_{{dm1}}} & 0 & 0 \\ 0 & {{x}_{{qm1}}} & 0 \\ 0 & 0 & {{x}_{{0m1}}} \\ \end{matrix} \right], $ | (2) |
| $ {\boldsymbol{X}_{13}}={\boldsymbol{X}_{24}}=\left[\begin{matrix} {{x}_{{dm2}}} & 0 & 0 \\ 0 & {{x}_{{qm2}}} & 0 \\ 0 & 0 & {{x}_{{om2}}} \\ \end{matrix} \right], $ |
| $ {\boldsymbol{X}_{ji}}=\boldsymbol{X}_{ij}^{\text{T}}, {\boldsymbol{X}_{{rr}}}=\left[\begin{matrix} {{x}_{{fd}}} & {{x}_{{fdkd}}} & 0 & 0 \\ {{x}_{{fdkd}}} & {{x}_{{kd}}} & 0 & 0 \\ 0 & 0 & {{x}_{{fq}}} & {{x}_{{fqkq}}} \\ 0 & 0 & {{x}_{{fqkq}}} & {{x}_{{kq}}} \\ \end{matrix} \right], $ |
| $ {\boldsymbol{X}_{ir}}=\left[\begin{matrix} {{x}_{{afdy}}} & {{x}_{{akdy}}} & 0 & 0 \\ 0 & 0 & {{x}_{{afqy}}} & {{x}_{{akqy}}} \\ 0 & 0 & 0 & 0 \\ \end{matrix} \right], $ |
| $ {\boldsymbol{X}_{{r}i}}=\boldsymbol{X}_{i{r}}^{{\rm T}} $ |
式中:f为励磁绕组;k为阻尼绕组;d为直轴;q为交轴;
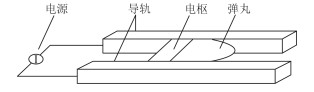
电磁轨道炮是一种典型的高能脉冲负载,它通过储能电容短时间内从电网平滑的吸收能量并存储,然后在ms级的时间内向轨道放电,使弹丸在很短的时间内加速到很高的速度,打破了传统火炮的出膛速度的限制[6-7]。其原理结构如图 2所示。
|
图 2 电磁轨道炮原理图 Fig. 2 Schematic diagram of electromagnetic railgun |
电磁轨道炮主要是由发射电源、导轨、电枢、弹丸等组成,在本质上是一种直线电机。其中,充电电源向发射电源提供发射所需要的能量;发射电源多由脉冲发电机、超级电容器等储能装置组成,用于在短时间内向系统提供发射所需的能量。储能电源通过开关及波形调整电感产生合适的脉冲电流为电磁轨道炮的发射供电。导轨导电并控制电枢和弹丸的运动方向。位于2条导轨之间的电枢通过洛伦兹力给弹丸加速至弹丸出膛。
2.2.2 电磁轨道炮的等效电路图由前述的轨道炮的原理图可以得到如图 3所示的等效电路图。在建模过程中做出2点假设:一是忽略电枢运动过程中的空气阻力和轨道摩擦力;二是认为轨道接入电路的电感和电阻大小的变化同电枢位移x的关系是线性的。在图 3中,Uc为电容器组电压,R0包括储能电容器组的内阻和线路电阻;L0为调波电感;Rx为电枢位移为x时轨道接入电路的电阻,Lx相应的电感,二者均随x而变化。

|
图 3 轨道炮等效电路图 Fig. 3 Equivalent circuit of railgun |
设流过电枢的电流为I(t),则在电枢运动过程中,轨道接入电路长度的变化引起轨道电感变化,进而引起的电压变化可以表示为:
| $ {{V}_{L}}=\frac{{\text{d}}\left( {{L}_{x}}I\left( t \right) \right)}{{\text{d}}t}={{L}_{x}}\frac{{\text{d}}I\left( t \right)}{{\text{d}}t}+I\left( t \right)\frac{{\text{d}}{{L}_{x}}}{{\text{d}}t}{\text{,}} $ | (3) |
因为Lx随x(t)线性变化,故Lx=L'x(t)则:
| $ \frac{{\text{d}}{{L}_{x}}}{{\text{d}}t}=\frac{{\text{d}}{{L}_{x}}}{{\text{d}}x(t)}\cdot \frac{{\text{d}}x(t)}{dt}={L}'\frac{{\text{d}}x(t)}{{\text{d}}t}{\text{,}} $ | (4) |
将式(3)代入式(2)得:
| $ {{V}_{L}}={{L}_{x}}\frac{{\text{d}}I(t)}{{\text{d}}t}+I(t)\frac{{\text{d}}{{L}_{x}}}{{\text{d}}t}={L}'x(t)\frac{{\text{d}}I(t)}{{\text{d}}t}+{L}'\frac{{\text{d}}x(t)}{{\text{d}}t}I(t){\text{。}} $ | (5) |
在图 3中,根据基尔霍夫电压定律并结合式(4)可以得到电磁轨道炮等效电路的微分方程,如式(5):
| $ {{U}_{c}}=({{R}_{0}}+{{R}_{x}})I(t)+{{L}_{0}}\frac{{\text{d}}I(t)}{{\text{d}}t}\!+\!{L}'x(t)\frac{{\text{d}}I(t)}{{\text{d}}t}\!+\!{L}'\frac{{\text{d}}x(t)}{{\text{d}}t}I(t){\text{。}} $ | (6) |
在图 2中, 整个电枢系统在t时刻聚集的能量可以由式(6)表示,其中x(t)表示电枢的位移。
| $ W=\int_{0}^{I(t)}{\lambda {\text{d}}I(t)}=\frac{1}{2}\cdot L\cdot I{{\left( t \right)}^{2}}{\text{。}} $ | (7) |
根据机电能量转换,电枢此时受到的洛伦兹力为:
| $ F=\frac{{\text{d}}W}{{\text{d}}x}=\frac{1}{2}\cdot I{{\left( t \right)}^{2}}\frac{{\text{d}}L}{{\text{d}}x}=\frac{1}{2}\cdot {L}'\cdot I{{\left( t \right)}^{2}}{\text{。}} $ | (8) |
根据牛顿第二定律可得:
| $ F=ma{\text{,}} $ | (9) |
| $ a=\frac{{\text{d}}v(t)}{{\text{d}}t}{\text{,}} $ | (10) |
| $ v=\frac{{\text{d}}x(t)}{{\text{d}}t}{\text{。}} $ | (11) |
结合式(7)~式(9)可以得到电磁轨道炮的运动学方程:
| $ m\frac{{\text{d}}v(t)}{{\text{d}}t}=\frac{1}{2}\cdot {L}'\cdot I{{\left( t \right)}^{2}}{\text{。}} $ | (12) |
电容器放电的数学模型可以由式(12)表示:
| $ \frac{{\text{d}}{{U}_{c}}}{{\text{d}}t}=\frac{I\left( t \right)}{C} $ | (13) |
式(5)、式(10)~式(12)即为简化的电磁轨道炮系统的数学模型。
2.3 其他设备模型由于本文主要是考虑脉冲负载对综合电力系统的影响,并且高阶的推进电机模块和逆变模块模型复杂阶次高,严重影响仿真的效率,因此,把建模重点放于发电整流模块和脉冲负载模块,对于推进和日常用电模块,用等值阻感负载模拟替代。
3 含高能负载的综合电力系统仿真分析根据第2节所述的简化的综合电力系统各模块的数学模型,在Matlab/simulink中建立相应的仿真模型。并将简化的电磁轨道炮模型嵌入简化的综合电力系统中进行全系统的仿真分析。其中2台带整流系统十二相同步发电机组成供电系统,容量整定为10 MW;系统的直流母线电压整定为4 000 V;推进电机由4 MW级阻感负载等效模拟;电磁轨道炮系统配置的容量整定为为4 MJ级。对系统进行运行性能仿真分析。
3.1 电磁轨道炮模型仿真与验证按式(5)、式(10)~式(12)所示电磁轨道炮数学模型在Matlab/simulink中搭建对应的仿真模型并进行仿真分析。其中所建立的模型初始化参数参照文献[8],如表 1所示。
|
|
表 1 电磁轨道炮系统主要参数 Tab.1 Main parameters of electromagnetic railgun |
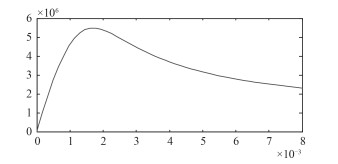
研究一个完整的发射周期内轨道炮的运行动态,仿真结果如图 4和图 5所示。
|
图 4 仿真模型中电枢的电流曲线 Fig. 4 Current waveform of the armature in the simulation model |

|
图 5 仿真模型中电枢的速度曲线 Fig. 5 Velocity waveform of the armature in the simulation model |
从图 4可看出,电枢电流峰值为5.5 MA,与文献[8]中的实验数据5.4 MA相符,误差在5%以内,同时曲线的走势与对比文献吻合较好;从图 5可看出,弹丸的出膛速度为2 686 m/s,与文献[8]中的实验数据2 600 m/s相符,误差在允许范围之内,曲线走势也吻合较好。仿真结果说明,在忽略空气、轨道等阻力情况下,只考虑轨道炮系统电气特性的模型能较好的反映轨道炮的动态特性,该模型可以用于进一步的研究。
3.2 全系统运行性能仿真在3.1节的基础上,将轨道炮的模型嵌入至简化的综合电力系统的模型中,进行运行性能仿真分析。分别在t=40 s,130 s,210 s时闭合开关,系统对轨道炮储能电容进行充电,充电结束后储能电容器组向电磁轨道炮系统放电,完成一个完整的发射周期后断开开关,并进入下一个发射周期。通过模拟3次完整的发射过程,来研究连续工作的高能脉冲负载对系统电能品质的影响。
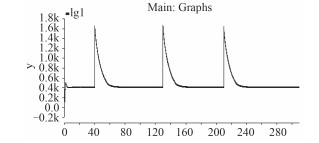
充电的过程中,在开关闭合的瞬间,由于储能电容器组的接入使得母线电压发生较大波动,并随着电容器组不断的充电而恢复稳定。电流从峰值1 700 A恢复到稳定时的400 A,如图 6所示。
|
图 6 直流母线变化曲线 Fig. 6 Current waveform of the DC bus |
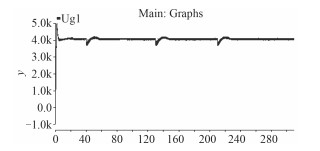
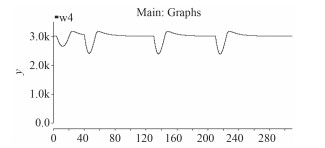
在每个充电周期内,直流母线电压受到较大的冲击,由4 000V降到3 500V,然后于3 s后恢复正常波动范围之内,如图 7所示。十二相同步发电机的转速同样有较大波动,跌落约20%,变化曲线如图 8所示。
|
图 7 直流母线电压变化曲线 Fig. 7 Voltage waveform of the DC bus |
|
图 8 发电机转速变化曲线 Fig. 8 Rotate speed waveform of the generator |
建立典型高能脉冲负载电磁轨道炮的数学模型,分析其动态特性,并进行仿真及对比验证,证明了模型正确。建立含高能脉冲负载的简化的综合电力系统模型并进行了仿真,结果表明,高能脉冲负载采用直接挂网运行的方式会对整个电力系统造成较大的冲击,影响系统的电能品质。
| [1] | MA W M. Development of vessel integrated power system[C]//Proceedings of the 14th International Conference on Electrical Machines and Systems. Beijing, China:IEEE, 2011. |
| [2] |
纪锋, 付立军, 王公宝, 等. 舰船综合电力系统飞轮储能控制器设计[J]. 中国电机工程学报 , 2015, 35 (12) :2952–2959.
JI Feng, FU Li-jun, WANG Gong-bao, et al. Controller design of flywheel energy storage for vessel integrated power systems[J]. Proceedings of the CSEE , 2015, 35 (12) :2952–2959. |
| [3] | HE Y, GUAN Y C, GAO G S, et al. Efficiency analysis of an electromagnetic railgun with a full circuit model[J]. IEEE Transactions on Plasma Science , 2010, 38 (12) :3425–3428. DOI:10.1109/TPS.2010.2082567 |
| [4] |
马伟明.十二相同步发电机及其整流系统的研究[D].北京:清华大学, 1995.
MA Wei-ming. Study of twelve-phase synchronous machine and its rectify system[D]. Beijing:Tinsghua University, 1995. http://www.oalib.com/references/16604349 |
| [5] |
纪锋, 王公宝, 付立军, 等. 十二相同步发电机降阶等效模型研究[J]. 电力系统保护与控制 , 2012, 40 (2) :28–33.
JI Feng, WANG Gong-bao, FU Li-jun, et al. Study on equivalent reduced model of twelve-phase synchronous generator[J]. Power System Protection and Control , 2012, 40 (2) :28–33. |
| [6] | MCNAB I R, FISH S, STEFANI F. Parameters for an electromagnetic naval railgun[J]. IEEE Transactions on Magnetics , 2001, 37 (1) :223–228. DOI:10.1109/20.911826 |
| [7] |
陈立学.电磁轨道炮电气负载特性的理论与实验研究[D].武汉:华中科技大学, 2007.
CHEN Li-xue. Theory and experimental research on electrical load characteristics of electromagnetic railgun[D]. Wuhan:Huazhong University of Science and Technology, 2007. http://cdmd.cnki.com.cn/article/cdmd-10487-2009037941.htm |
| [8] | TAHER A B, JAFARI M, PAKDEL M. A new approach for modeling electromagnetic railguns[J]. IEEE Transactions on Plasma Science , 2015, 43 (5) :1733–1742. DOI:10.1109/TPS.2015.2419272 |
 2016, Vol. 38
2016, Vol. 38
