2. 海军工程大学 舰艇装备仿真技术研究室, 湖北 武汉 430033
2. Institute of Naval Power Plant Simulation, Naval University of Engineering, Wuhan 430033, China
由于舰艇动力平台系统复杂使命任务特殊且经常会在复杂海况条件下运行,因此系统损坏、任务改变或环境变化等各类事件时有发生。在日常操作使用过程中,舰艇操作人员在处理这类时变不确定性信息时存在较大困难,特别是在出现重大险情又需舰艇保持动力不能立即停机停炉时对指挥员的处置能力考验非常大。主冷凝器作为蒸汽动力系统的关键设备将汽轮机排出的废气冷凝成水经除氧加热后输送给锅炉形成给水凝水闭环,如在工作中冷凝器发生故障不能正常运行,若不能够及时排出故障将会造成重大装备损伤,后果不堪设想[1]。
贝叶斯网络(Bayesian Network,BN)是不确定性问题推理的重要理论模型,采用有向图(Directed Acyclic Graph,DAG)来描述事物间概率关系的图模型(Graph models)[2],又称为因果关系网和信度网,模型以节点作为变量,边表示变量之间相互依赖关系[3]。1993年,Xiang教授在贝叶斯网络基础上提出了多连片贝叶斯网络(Multiple Sectioned Bayesian Networks,MSBN),将模块化和面向对象思想引入到贝叶斯网络中,可以把一个大的系统分解为几个子系统进行求解,利用单个智能体进行分布式自主推理,随后利用多个智能体间重叠子域紧凑的消息传播,实现多智能体协同推理[4 -6]。
本文提出将MSBN方法应用到舰船主冷凝器故障建模中,由主冷凝器损伤的因果关系建立故障损伤模型,最后进行实例研究。
1 贝叶斯网络及多连片贝叶斯网络的静动态形式静态贝叶斯网络(Bayesian Nets,BNs)是一个三元组(V,G,P),V为所有变量的集合,G为贝叶斯网络中所有有向无环图的集合[7],P为任一节点的概率:
| ${\rm{\pi }} P=\left\{ P(v\left| {\rm{\pi }} (v) \right.)\left| v\in V \right. \right\}, $ | (1) |
式中:
动态贝叶斯网络(Dynamic Bayesian Nets,DBNs)是一个四元组[8]
| $ G=\left( \underset{t=0}{\mathop{\bigcup }}\, {{V}_{t}}, \underset{t=0}{\mathop{\bigcup }}\, {{E}_{t}}, \underset{t=0}{\mathop{\bigcup }}\, E_{t}^{\to }, \underset{t=0}{\mathop{\bigcup }}\, {{P}_{t}} \right), $ | (2) |
式中:Vt为动态域中t(0≤t<k)时刻的变量;
| $ {P_t}\left\{ \begin{array}{l} P({V_0}), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t = 0\text{;}\\ P({V_t}\left| {F{I_{t - 1}}} \right.)\;\;{\rm or}\;\;P(B{I_{t + 1}}\left| {{V_t}} \right.)\;\;\;\;t > 0\text{。} \end{array} \right. $ | (3) |
多连片贝叶斯网络(MSBN)可以表示为三元组M=(V,G,P),
| $ P=\underset{i}{\mathop{\Pi }}\, {{P}_{{{G}_{i}}}}({{N}_{i}})\text{,} $ | (4) |
变量集Vi的联合概率分布为:
| $ {{P}_{{{G}_{i}}}}=\underset{X\in {{N}_{i}}}{\mathop{\Pi }}\, {{P}_{{}}}(X\left| Pa(x) \right.)\text{。} $ | (5) |
|
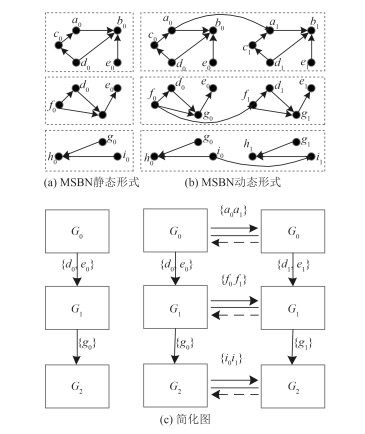
图 1 MSDBN示意图 Fig. 1 Schematic diagram of MSDBN |
动态多连片贝叶斯网络(MSDBN)是MSBNs在时间序列上由初始网经转移网形成的动态网,表示形式同DBNs相似。
| $ M=\left( \underset{t=0}{\mathop{\bigcup }}\, {{V}_{t}}, \underset{t=0}{\mathop{\bigcup }}\, {{E}_{t}}, \underset{t=0}{\mathop{\bigcup }}\, E_{t}^{\to }, \underset{t=0}{\mathop{\bigcup }}\, {{P}_{t}} \right)\text{。} $ | (6) |
式中:
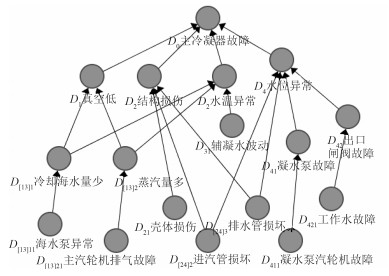
图 2是主冷凝器单个时间片损伤贝叶斯故障模型G0,每个节点状态用圆圈表示,相互间的逻辑关系用连接线表示,网络结构共有4层。
|
图 2 主冷凝器贝叶斯网络故障模型 Fig. 2 The BN fault model of main condenser |
第1层为主冷凝器故障(D0);第2层由真空低(D1)、结构损伤(D2)、水温异常(D3),和水位异常(D4)组成;第3层由冷却海水量少(D[13]1)、蒸汽量多(D[13]1)、辅凝水波动(D31)、壳体损伤(D21)、进汽管损坏(D[24]2)、排水管损坏(D[24]3)、凝水泵故障(D[24]3),出口闸阀故障(D42)组成;第4层由海水泵异常(D[13]11)、主汽轮机排气故障(D[13]21),凝水泵汽轮机故障(D411)组成。底事件D[13]1,D[13]1是D1和D3的共同节点,D[24]2,D[24]3是D2和D4的共同节点,为了减少网络规模将其合并成一个节点。
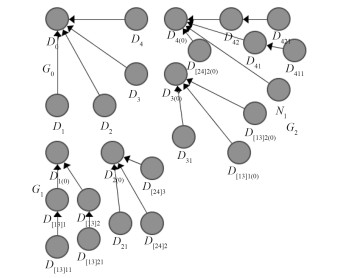
按照前述MSBN的建模方法,利用变量之间的相互依赖关系将模型进一步重构划分为3个模块G0,G1,G2,如图 3所示。每个模块既是独立的贝叶斯网络可以同相邻的模块进行交互通信,使网络具备子模块的局部推理及总模块的全局推理,实现MSDBN的协同推理。G0和G1之间的通信变量为{D1,D2},G0和G3之间的通信变量为{D3,D4}。
|
图 3 主冷凝器MSBN模型 Fig. 3 The MSBN model of main condenser |
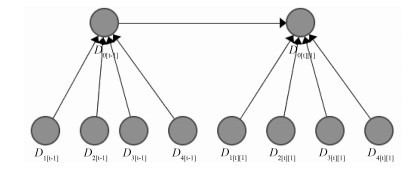
由于时间T内的动态过程服从一阶Markov假设和时齐性的特点,可以将其在T时间内展开成n个单时间片(MSDBN1,MSDBN2…MSDBNn)的动态过程,如图 4所示,对于结构不变的MSDBN,每个时间片的网络结构不变,变量之间的相互关系不变,但转移概率可能发生变化。
|
图 4 MSDBN模型 Fig. 4 MSDBN model |
MSDBN模型参数设定方法有多种,主要有基于Monte Carlo仿真方法、基于Weibull分布的装备概率确定方法及专家经验确定方法。对于前面所建的主冷凝器MSDBN模型,概率采用装备维修专家和装备日常管理使用经验的综合数据采样进行确定。表 1是D0,D1,D2,D3,D4的状态转移概率B1→,B2→,B3→,B4→。由于在固定时间片内网络结构和变量间的相互关系不变,假定条件概率也不变。
|
|
表 1 状态转移概率 Tab.1 Transition conditional probability |
1)实验1:验证模型的准确性
实验仿真主冷凝器战损模式下部分传感器发生故障和数据缺失时应用MSDBN进行系统状态监测和故障诊断。主冷凝器在某次运行过程中发生异常导致主冷凝器健康状态报警,初始化主冷凝器损伤模型各节点概率,传感器观测到了4个时间片上的部分数据,如表 2所示。
|
|
表 2 观测数据 Tab.2 Observation data |
根据实验数据得出P(D0)=0.867 4,如图 5所示。通过改变各节点的底层概率,观察概率值变化,实验中其他参数不变,将P(D[13]11)的概率由0.86升为0.93,得出P(D0)的概率为0.915 9;其它参数不变将将P(D[13])由0.94降为0.87,得出P(D0)的概率为0.825 9。实验概率计算结果同实际相符,通过改变底事件节点概率得到的顶事件节点概率趋势正确,因此使用MSBN的建模方法可行。

|
图 5 概率计算结果 Fig. 5 Probability calculation results |
2)实验2:通过故障现象分析故障原因
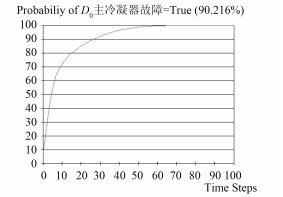
运行过程中实时监控主冷凝器的运行状态。某一时刻发现主冷凝器出现损伤故障,并且故障一直未消除,主冷凝器的概率随时间变化趋势如图 6所示。
|
图 6 节点D0的概率值曲线 Fig. 6 Probability value curve of node D0 |
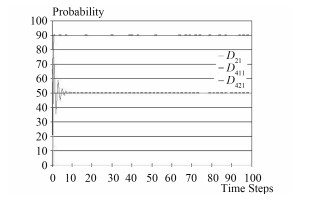
检查各底事件的状态值,随时间变化趋势如图 7所示,主冷凝器开始出现故障的瞬时原因主要是由于节点D421工作水发生故障导致主冷凝器闸阀不能完全打开出现主冷凝器出水不稳,在10个时间步长以后闸阀打开,水流通畅,随着时间推移最终导致主冷凝器发生损伤的主要原因是凝水泵汽轮机节点D411发生故障引起凝水泵本体故障进而引起水温异常,此时应果断采取措施起动备用凝水泵,关闭当前凝水泵并组织抢修。
|
图 7 底事件概率值曲线 Fig. 7 Probability value curve of bottom event |
本文针对主冷凝器故障诊断的复杂性提出了使用贝叶斯建模方法解决,建立了动态多连片网络模型,设定了相关参数,通过实验分析得出以下结论:
1)贝叶斯网络建模可以运用于舰船主冷凝器故障诊断,通过建立的贝叶斯网络模型可以清晰表达引起主冷凝器故障的各因素之间的关系,通过初始化各节点的概率可以实时监控其状态。
2)在静态贝叶斯网络基础上引入时间序列建立动态贝叶斯网络模型可以更准确反应每个时间片的状态信息,提高模型的准确性,增强实时性。
3)不仅能够进行从故障原因到现象的正向推理,还能进行故障现象到原因的反向推理,可为蒸汽动力设备的故障诊断提供有效决策。
| [1] |
初珠立, 杨自春, 梁洁, 等. 主冷凝器损伤的模糊随机特性及贝叶斯网络分析[J]. 哈尔滨工程大学学报 , 2012, 33 (12) :1217–1222.
CHU Z L, YANG Z C, CHEN G B, et al. Damage analysis of the main condenser based on fuzzy random Bayesian networks[J]. Journal of Harbin Engineering University , 2012, 33 (12) :1217–1222. |
| [2] | 李海军, 马登武, 刘霄, 等. 贝叶斯网络理论在装备故障诊断中的应用[M]. 北京: 国防工业出版社, 2009 . |
| [3] |
陈海洋, 高晓光, 樊昊. 变结构DDBNs的推理算法与多目标识别[J]. 航空学报 , 2010, 31 (11) :2222–2227.
CHEN H Y, GAO X G, FAN H. Reasoning algorithm of variable structure and target recognition[J]. Acta Aeronautica Etastonautica , 2010, 31 (11) :2222–2227. |
| [4] | Y XIANG. Comparison of mutiagent inference methods in multiply sectioned Bayesian networks[J]. International Journal of Approximate Reasoning , 2003, 33 :235–254. DOI:10.1016/S0888-613X(03)00017-3 |
| [5] | Y XIANG. A probabilistic framework for cooperative multi-agent distributed interpretation and optimization of communication[J]. Artificial Intelligence , 1996, 87 :295–342. DOI:10.1016/0004-3702(95)00110-7 |
| [6] | AN Xiang-dong, YANG Xiang, NICK C. Dynamic multiagent probabilistic inference[J]. International Journal of Approximate Reasoning , 2008, 48 :185–213. DOI:10.1016/j.ijar.2007.08.010 |
| [7] |
苏艳琴, 徐廷学, 张文娟. 粗糙集和贝叶斯网络融合故障诊断方法[J]. 舰船科学技术 , 2013, 35 (3) :91–93.
SU Y Q, XU T X, ZHANG W J. Rough sets and Bayesian network fusion fault diagnosis methods[J]. Ship Science and Technology , 2013, 35 (3) :91–93. |
| [8] |
付尧, 曾凡明, 陈于涛, 等. 舰用柴油机冷却水系统贝叶斯状态推理方法[J]. 舰船科学技术 , 2014, 36 (8) :42–45.
FU Yao, ZENG Fan-ming, CHEN Yu-tao. Study on the bayesian reasoning methods for marine disel chill water system[J]. Ship Science and Technology , 2014, 36 (8) :42–45. |
 2016, Vol. 38
2016, Vol. 38
