齿轮传动装置已被广泛应用于舰船、航天、汽车、风电等工业和国防领域,是工业产品和国防装备的重要部件,也是装备振动与噪声的主要来源之一。随着现代舰船推进齿轮系统朝着高速、重载的方向发展,齿轮轮齿的热变形和弹性变形显著增加,其支撑系统的变形相应增大;且在制造和安装过程中不可避免的产生误差,使理论上等价于2个基圆作纯滚动的渐开线齿轮发生非共轭啮合,导致齿轮传递的载荷、速度发生波动,从而降低传动精度,增加了振动与噪声。舰船推进齿轮系统过大的噪声会降低舰船的声隐身性,较大的振动会影响设备本身的安全稳定性。为了控制振动和噪声,通常采用齿轮修形的方法。
Walker[1]最先提出了齿轮修形概念,之后众多学者对修形做了许多的试验研究。H.Sigg[2]提出了啮合冲击及影响啮合冲击的因素,获得了齿廓最大变形量和修形长度的公式并加以验证。Yoshino Hidehir等[3]对加工螺旋齿、斜齿轮的滚刀进行轴向修形设计,利用此方法产生的传动误差较小,从齿轮加工出发也为齿轮修形技术发展提供新的方向。方宗德等[4]以最小传动误差为目的,对齿廓修形曲线参数进行优化设计,通过试验对比修形前后的传动误差,证明优化的齿廓修形能有效地降低传动误差。常山[5]通过有限元软件获得齿轮啮合不同位置的接触应力和齿廓变形,提出齿廓修形的方案。王文杰等[6]对有限元软件Ansys进行了二次开发,设计了齿轮修形程序,输入参数即可得接触分析及修形方案。
目前,国内外的公司针对齿轮的修形,大多数是利用经验公式,学者对于齿轮修形的研究,大部分只考虑齿轮的弹性变形,忽略其热变形量,而高速、重载齿轮其热变形量较大,不能忽略不计。本文针对此问题,建立齿轮的齿面温度场有限元模型,分析提取热变形;根据轮齿的热弹变形确定齿轮三维修形参数。并且,结合试验结果验证了修形参数有效性,为齿轮系统减震降噪设计提供了依据。
1 温度场分析及热变形为了获得高速斜齿轮的热变形量,需要先分析齿轮本体温度场。本文利用商业有限元软件Ansys进行有限元分析。齿轮参数如表 1所示。
|
|
表 1 斜齿轮参数 Tab.1 Parameters of helical gear |
本文齿轮润滑采用的是L-TSA32汽轮机油,在40 ℃时相关的参数特性如表 2所示,
|
|
表 2 润滑油物理参数 Tab.2 The physical parameters of lubricating oil |
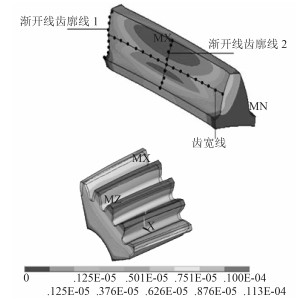
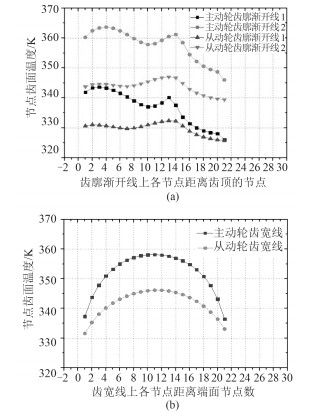
分析轮齿上温度分布情况,如图 1所示,分别提取主、从动轮上2条齿廓渐开线以及一条节圆齿宽线上的温度。从图 2中可以看出:①模型中同一节点上,主动轮的温度都高于从动轮。本模型中主动轮为小齿轮,小齿轮的啮合次数较多,所以小齿轮的温度高于大齿轮温度。②斜齿轮温度场的分布规律为:齿廓上,齿轮节圆附近并不是最高温度区域,齿轮的最高温度出现在齿顶附近或者齿根附近。齿廓线上的节点的温度,从齿顶到齿根都是先上升再下降,在齿顶附近达到高值;之后温度继续上升,在齿根附近到达高值,然后再下降。③斜齿轮温度场的分布规律:在齿向方向上,轮齿的温度先升高后降低,在半齿宽附近处温度达到最高值。
|
图 1 齿轮温度场及热变形 Fig. 1 Temperature and thermal deformation of gears |
|
图 2 齿面温度分布情况 Fig. 2 Temperature and thermal deformation of gears |
稳态热分析之后获得节点温度,保存热分析结果文件并删除热载荷、约束方程等。更改单元分析选项,建立与温度场单元具有相同网格节点号的结构单元。定义材料特性,如热膨胀系数。在结构分析中,由将本体温度场作为体载荷加载,限制底面的所有自由度,限制2个侧面的轴向和周向的自由度,最终在结构应力分析环境下求解得到仅考虑温度影响的齿轮热变形云图。齿面热变形量的分布规律与齿轮温度场分布规律完全一致。
2 斜齿轮修形参数确定常见的齿轮修形包括齿廓、齿向和三维修形。
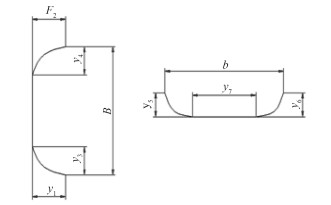
如图 3所示,左右分别为小齿轮的齿廓、齿向的二维修形曲线。在齿高方向上,对小齿轮的齿顶和齿根进行齿廓修形。其中,y1和y2分别为齿根、齿顶最大修形量,y3和y4分别为齿根、齿顶的修形长度,y5和y6分别为齿向啮入、啮出的最大修形量,y7为齿向不修形长度,H和b为齿高和齿宽。修形曲线为四次抛物线。齿廓与齿向修形的叠加即为三维修形。
|
图 3 齿廓修形(左),齿向修形(右) Fig. 3 Profile modification, axial modification |
在对轮齿进行弹性修形时,考虑时间经验及加工方便,各国各公司都有自己的经验计算公式及标准。这里弹性修形量的确定采用文献[7]中提到的方法,齿面优化修形是基于传动误差-冲击-振动最小为目的。利用程序软件,对表 1参数的齿轮进行优化,得到修形参数如表 3所示,单位为m。
|
|
表 3 考虑弹性变形的齿轮修形参数 Tab.3 The physical parameters of lubricating oil |
进行有限元温度场分析后,提取斜齿轮热变形量。如图 4为五齿-齿轮模型的端面图,获得空间上的微小变形量分别沿着x,y,z轴3个方向,变形量大小依次为ux,uy及uz。但研究对象为最中间轮齿(第3个轮齿),且研究的热变形量为仅考虑oxy平面中变形量ux,uy沿着啮合线方向的分量∆s,所以在此需对所提取的微小热变形数据ux,uy及uz进行相应处理。
|
图 4 有限元模型的齿轮端面图 Fig. 4 Finite element model of the gear face figure |
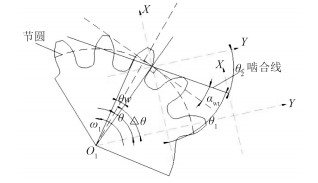
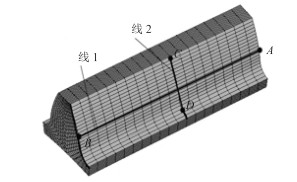
其中,如图 5所示,齿宽线为节圆圆柱与齿面的交线,齿廓渐开线2为半齿宽处的齿廓线。在线1上,将点A、点B处的热变形量∆s作为齿向修形的热修形量y5,y6;在线2上,将点C(啮出点)、点D(啮入点)处的热变形量∆s作为齿廓修形的热修形量y2,y1。所以,如图 4所示,中间齿在端面上的任一节点(包括B点)的热变修形量∆s为:
| $ \Delta s=uy\cos {{\theta }_{2}}-ux\cos {{\theta }_{1}}=uy\sin {{\theta }_{1}}-ux\cos {{\theta }_{1}}。 $ | (1) |
|
图 5 轮齿有限元模型 Fig. 5 The finite element model of gear tooth |
通过有限元分析计算,得到模型中各个节点的位移,最后得到热变形修形量数值,如表 4中所示。
|
|
表 4 考虑热变形的齿轮修形参数 Tab.4 The physical parameters of lubricating oil |
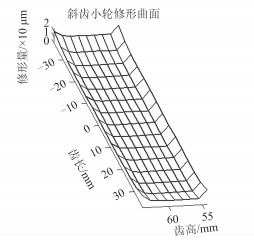
将分别考虑齿轮弹性变形和热变形的齿轮修形参数进行叠加,得到新的修形方案,即考虑齿轮热弹性的齿轮修形,如表 5所示,修形曲面如图 6所示。
|
|
表 5 考虑热弹变形齿轮修形参数 Tab.5 The modification parameters of lubricating oil |
|
图 6 小齿轮修形齿面 Fig. 6 The modified curved surfaces of small gear |
试件为表 1参数修形后的斜齿轮。试验采用的是机械式封闭功率圆柱齿轮振动试验台。主要试验部件:调速电机、扭矩仪、加载器、试验箱、陪试箱、圆光栅、支架、数据采集卡。试验台的现场布置如图 7所示。

|
图 7 试验台现场布置 Fig. 7 Test beneh |
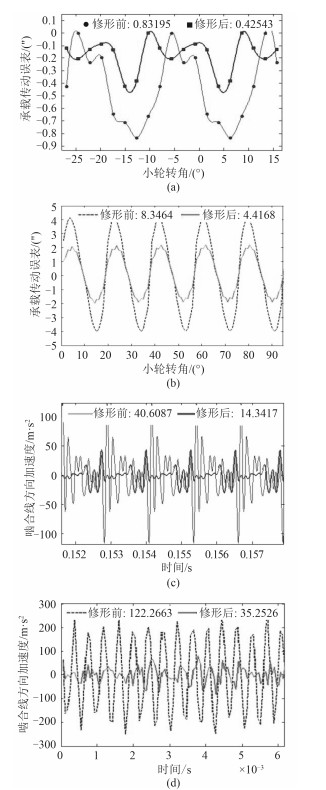
图 8(a)和图 8(b)分别为光栅测量传动误差与理论仿真的比较;图 8(c)和图 8(d)分别为齿轮副啮合线方向相对振动与理论仿真的比较。可以发现,修形后的齿轮传动误差幅值由8.346 4降低至4.416 8,降低达到了47.08%,而啮合线方向加速度幅值均方根由122.266 3 m/s2降低至36.252 6 m/s2,降低达到了70.35%。试验结果证明,采取热弹修形的齿轮在降低噪音和振动方面起到了很好的效果。
|
图 8 理论与试验数据对比 Fig. 8 Comparison of theoretical and experimental data |
本文建立斜齿轮有限元温度场模型,分析齿面温度场分布及热变形情况,提取热变形量与弹性变形量叠加,得到考虑齿轮热-弹变形的齿轮修形曲线,并利用试验论证其修形效果。对于高速重载齿轮提出的这种新的修形方法,是在齿轮弹性修形基础上,通过建立精确地齿轮温度场有限元模型,仿真获得较为准确的节点热变形量,叠加在弹性变形上得到新的修形曲线,利用试验证明了其在减振降噪、提高齿轮传递品质上的优越性。
| [1] | WALKER H. Gear tooth deflection and profile modification[J]. Engineer , 1938, 166 :434–436. |
| [2] | SIGG H, Maag Grear-Wheel Company Ltd. Profile and longitudinal corrections on involute gears[C]//The Semi-Annual Meeting of the AGMA. Chicago:AGMA, 1965. |
| [3] | YOSHINO H, MUTA Y. Studies on 3-D tooth surface modification of helical gears[J]. Transactions of the Japan Society of Mechanical Engineers. part C , 1996, 62 (2) :595–598. |
| [4] | 方宗德, 张永才, 蔺天存. 斜齿轮的齿廓修形的实验研究[J]. 机械传动 , 1992, 16 (4) :27–30. |
| [5] | 常山, 陈谌闻, 李威, 等. 重载齿轮齿面接触应力分布及轮齿修形[J]. 矿山机械 , 1995 (11) :21–24. |
| [6] | 王文杰.风机增速器斜齿轮啮合载荷及齿向修形的研究[D].大连:大连理工大学, 2007. http://cdmd.cnki.com.cn/article/cdmd-10141-2008034801.htm |
| [7] | 蒋进科, 方宗德, 苏进展. 基于承载传动误差幅值最小的斜齿轮齿面修形优化设计[J]. 航空动力学报 , 2013, 28 (7) :1637–1643. |
 2016, Vol. 38
2016, Vol. 38
