作为舰船主要噪声源之一的动力齿轮传动装置,除了满足其功能和可靠性外,还应该满足低振动噪声的要求。因此,齿轮传动装置振动噪声直接关系到舰船的整体性能,控制齿轮传动装置的振动与噪声己成为重要的研究课题。一般来说,有2种措施可以减少齿轮传动装置的振动以及噪声辐射:1)控制振动激励源:在齿轮设计、加工阶段采取减振降噪措施,有助于从噪声的源头消除其形成。通过优化齿轮设计参数,提高齿轮加工安装精度降低齿轮振动的激励力。2)控制振动传递途径:在振动噪声传递途径中衰减它,通常通过齿轮弹性安装,添加阻尼材料等。其中,通过齿轮优化设计控制振动激励源是从源头上采取措施,是治本的方法[1]。
MASTA软件作为一种齿轮传动系统设计分析软件,有较强的计算分析功能和参数优化功能,可以准确计算齿面接触应力和齿轮传递误差。它的宏观参数优化和微观修形模块为齿轮低噪声设计提供了便利条件,本文以某试验齿轮传动装置为研究对象,阐述MASTA软件在低噪声齿轮传动装置设计分析中的应用方法与技术。首先归纳了齿轮各设计参数对振动噪声的影响,然后介绍齿轮优化设计中常用目标函数重合度、安全系数、传递误差与设计变量之间的函数关系,最后针对某试验齿轮传动装置,使用MASTA软件对其进行齿轮参数优化设计,提高了齿轮强度,降低了传递误差。再运用MASTA软件对优化后的齿轮进行修形设计,进一步降低其传递误差,实现了低噪声设计。
1 齿轮低噪声设计概述 1.1 齿轮设计参数对振动的影响[2 -3]1)模数
齿轮的刚度一般随着模数的增大而增强,对于大功率的齿轮传动装置,齿根弯曲变形是主要影响因素,因此选用较大模数,增加齿轮的刚度,减少齿轮传递误差,有利于降低其振动噪声。
2)压力角
减小压力角,可以增加轮齿的柔性,降低了动态激励,从而有利于噪声的降低。
3)螺旋角
斜齿轮随着螺旋角的增大,重合度增大,噪声降低,但是当螺旋角太大时其降噪效果较螺旋角较小时要差,通过最优螺旋角的选择,可以大大改善齿轮的动态特性。
4)重合度
增大重合度可以减小单对轮齿的负荷,从而减小啮入和啮出的负荷冲击,降低齿轮噪声,并且减小轮齿的动态激励。此外,几乎所有对齿轮噪声有影响的轮齿参数,实际上都是由于它们对重合度的影响而起作用的,因此增大齿轮重合度是最重要的参数设计方法。
1.2 齿轮传动优化目标函数[4]1)弯曲安全系数SFmin
齿轮有多种失效形式,但其中危害最大的是轮齿折断,对于齿根安全系数越大越好,特别是对于舰用齿轮传动装置。
2)接触安全系数SHmin
齿轮传动另外一种很重要的失效形式点蚀,点蚀是齿面疲劳损伤的现象之一,它成为限制齿轮承载能力和使用寿命的关键因素。
3)重合度
重合度是影响齿轮振动噪声的重要因素,齿轮设计要求尽可能提高齿轮重合度,以保证在传动过程中同时有2对或更多对轮齿参与啮合,从而使传动更加平稳、噪声更低。
4)载荷分布情况
当一对齿轮啮合时,由于轮齿、传动轴、箱体受载变形以及制造安装误差的存在,往往会出现沿齿宽方向受载不均,甚至出现偏载现象,使局部齿廓承受非常大的应力,降低了齿轮的承载能力,加快齿轮表面的磨损,载荷分布与齿轮的基本参数,例如齿宽、螺旋角等有很大的关系。
5)传递误差TE
齿轮传递误差是齿轮系统振动和噪声的激励源,由于轮齿受载弹性变形引起的传动误差,它仅与齿轮的设计参数有关,故而称为“设计传递误差”。降低传递误差(TE)幅值,既能减少齿轮副啮合的动载荷,进而减少噪声,同时可以降低强度计算中的动载系数(Kv),从而提高齿轮副的寿命。
2 基于MASTA齿轮设计参数优化 2.1 齿轮参数优化方案为了提高齿轮装置的可靠性,并且降低其振动噪声,本文参数优化的目标为齿轮的接触安全系数、弯曲安全系数以及齿轮的重合度。从齿轮重合度计算公式可知,当齿轮齿数和啮合角一定时,齿顶圆压力角主要受齿顶高系数的影响,齿顶高系数越大,齿顶圆压力角就越大,齿轮重合度也越大,传动越平稳。因此,齿顶高系数在传动指标中主要影响齿轮重合度。对于斜齿轮主要是影响端面重合度,端面重合度对降低齿轮噪声、增加传动平稳性具有明显效果,本文只优化端面重合度。
从齿轮重合度计算公式可知,当齿轮齿数和啮合角一定时,齿顶圆压力角主要受齿顶高系数的影响,齿顶高系数越大,齿顶圆压力角就越大,齿轮重合度也越大,传动越平稳。因此,齿顶高系数在传动指标中主要影响齿轮重合度,对斜齿轮主要是影响端面重合度。MASTA可以提供多种齿轮参数优化方案,本文结合实际情况,选用2种优化方案,优化前后齿轮参数对比见表 1。
|
|
表 1 齿轮参数优化方案比较 Tab.1 Comparison of different cases of gear optimization |
运用MASTA软件和Ansys软件,对表 1所示的3组齿轮参数进行强度分析和传递误差计算。强度计算的结果如表 3所示,优化后齿面应力分布如图 1所示,传递误差如图 2所示。
|
|
表 2 各方案齿轮设计参数表 Tab.2 Gear design parameters for different cases |
|
|
表 3 参数优化后齿轮计算结果对比 Tab.3 Comparison of numerical results for different cases after optimization |
|
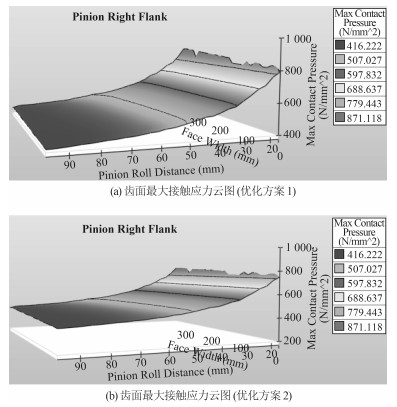
图 1 优化前齿轮齿面接触应力云图 Fig. 1 Contour of gear flank contact stress after optimization |
|
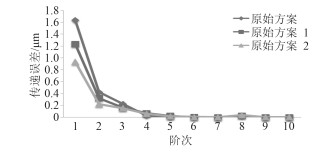
图 2 参数优化后的传递误差比较图 Fig. 2 Comparison of gear TE after optimization |
从表 3及图 1可看出,2种优化方案的齿轮副重合度提高到一个较大值,方案一的端面重合度提高了58.12%,传递误差降低25.32%;齿轮强度也进一步提高,小齿轮接触安全系数提高了28.65%、弯曲安全系数提高了5.6%,大齿轮接触安全系数提高了9.55%、弯曲安全系数提高了26%;
由于方案2的优化变量中增加了螺旋角和压力角,优化的结果更好,方案2的重合度提高了62.32%,传递误差降低38.21%;强度方面,小齿轮接触安全系数提高了32.02%,弯曲安全系数提高了15.16%,大齿轮接触安全系数提高了11.7%,弯曲安全系数提高了33.5%。
3 低噪声齿轮修形设计 3.1 齿轮修形方式[5 -8]为了进一步降低振动噪声,在齿轮设计参数优化方案2的基础上,利用MASTA软件进行修形设计。齿轮修形不但可以改善传动性能、提升齿轮的承载能力,而且对于降低齿轮传动噪声有着重要的影响。然而,对于修形量的给定,现阶段还没有比较精确的计算式。
3.1.1 齿廓修形方式对于齿廓修形,目前工程上主要采用下列2种计算式:
1)以齿轮的受载变形来确定齿廓修形量
| $ {{\Delta }_{\max }}={{\delta }_{s}}=\frac{{{\omega }_{t}}}{{{c}_{\gamma }}}=\frac{{{F}_{t}}}{{{c}_{\gamma }}b}, $ | (1) |
式中:δs为齿廓弹性变形量;ωt为单位齿宽载荷;Ft为齿轮分度圆上的切向力;b为齿轮有效宽度;cγ为轮齿的啮合刚度;cγ可依据ISO6336-2006求得。
2)以齿轮的制造精度来确定齿高修形量
| $ {{\Delta }_{\max }}=0.02{{m}_{n}}, \ {{h}_{\max }}=0.6{{m}_{n}}。 $ | (2) |
1)齿端倒坡,一般倒坡长度取L1=0.15 b,L2=0.1 b,13 μm≤∆≤35 μm。
2)鼓形齿,对于这种修形方式,ISO给出了2种可供选用的参数值。第1种,对于普通齿轮,10 μm≤∆≤40 μm,另加制造公差5 μm;对于高精度齿轮,0 μm≤∆≤25 μm,另加制造公差5 μm。第2种,可取∆ ≈ 0.5 Fβxcv,其中,Fβxcv是等效啮合歪斜度,在数值上等于未修形齿的原始啮合歪斜度Fβx
3)齿向修形与两端倒坡同时进行。
可以看出,无论是齿廓修形还是齿向修形,现有的标准均只给出了一个取值范围,对于具体情况,可能并不完全适用。然而修形不恰当反而会进一步降低齿轮的传动性能,起到相反的效果。
3.2 齿轮修形计算本文采用有限元法,考虑了整个传动系统的变形,使用MASTA软件完成方案2的齿轮修形设计。由于大齿轮齿数较多,修形经济性能不好。因此齿廓修形时对小齿轮做齿顶齿根同时修形,中间保留一段长度不修形,一方面是为了保证重合度大于1,另一方面与载荷沿啮合线分布偏中部有关。
根据公式计算,齿顶修形量为46 μm,齿根修形量均为39 μm。对于齿向修形,采用小齿轮两端齿向倒坡修形,修形长度为28.5 mm,修形量为15 μm,修形曲线分别采用二次曲线和直线,比较二次曲线与直线的修形效果。
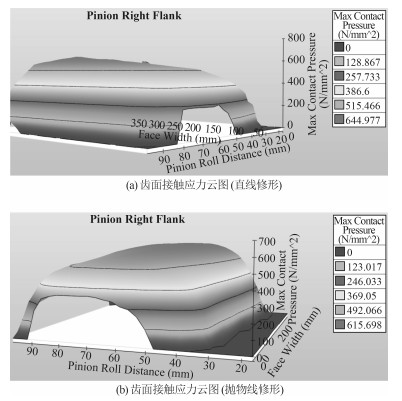
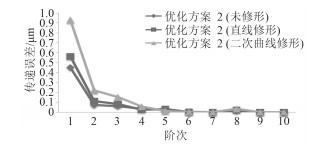
齿廓和齿向都采用直线修形后最大接触应力如图 3(a)所示,齿廓和齿向都采用二次曲线修形后最大接触应力如图 3(b)所示,2种修形后传动误差对比如图 4所示。
|
图 3 优化方案2修形后齿轮齿面接触应力云图 Fig. 3 Contour of gear flank contact stress after optimization for case Ⅱ |
|
图 4 修形后的传递误差比较图 Fig. 4 Comparison of gear TE after optimization |
对于采用直线修形,修形后齿轮啮合副沿齿宽方向载荷分布更为均匀,其最大接触应力由822.8 N/mm2降到了644.9 N/mm2,降低了21.65%;传递误差由0.92 μm降到0.57 μm,降低了38.04%。
采用二次曲线修形比采用直线修形的齿面接触更均匀,特别是在修形区域,其最大接触应力由822.8 N/mm2降到了615.6 N/mm2,降低了25.18%;递误差由0.92 μm降到0.49.78 μm,降低了44.34%,可以看出齿轮啮合副采用二次曲线修形比直线修形效果更好。
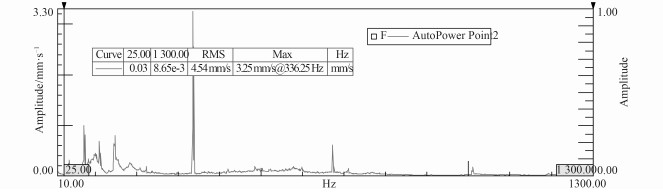
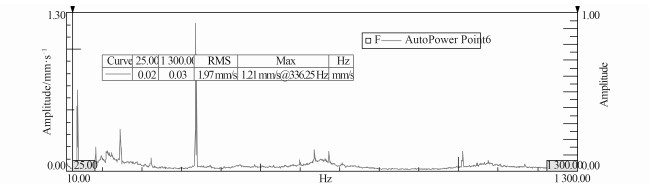
4 齿轮修形试验验证为了验证MASTA低噪声修形设计,在功率封闭单斜齿轮实验台上对未修形、直线修形以及二次曲线修形齿轮进行了振动测试,试验台布置图 5所示,实验工况为封闭功率1 000 kW,小齿轮转速550 r/min,试验结果如图 6~图 8所示。采用直线修形,其最大振动速度由未修形的3.25 mm/s降到1.21 m/s,降低了58.2%。采用二次曲线修形,其最大振动速度由未修形的3.25 m/s降到0.80 m/s,降低了74.8%。这可以验证了MASTA修形的可靠性,同时也得出齿轮啮合副采用二次曲线修形比直线修形效果更好。

|
图 5 单斜齿轮功率封闭试验台 Fig. 5 single helical gears power circulatory test rig |
|
图 6 齿轮箱啮合力方向振动速度图谱(优化方案2 —未修形) Fig. 6 Spectrum of gear vibration velocity in the direction of engaging force(case 2-without modification) |
|
图 7 齿轮箱啮合力方向振动速度图谱(优化方案2 —直线修形) Fig. 7 Spectrum of gear vibration velocity in the direction of engaging force(case 2-linear profile modification) |

|
图 8 齿轮箱啮合力方向振动速度图谱(优化方案2 —二次曲线修形) Fig. 8 Spectrum of gear vibration velocity in the direction of engaging force(case 2-parabolic profile modification) |
本文以某齿轮传动装置为研究对象,利用MASTA及Ansys软件校核了齿轮强度、计算了传递误差,采用不同的齿轮参数优化设计方案,对比了不同方案的优化结果,证明优化的变量越多其优化的效果越好。在方案优化的基础上采用二次曲线、直线2种修形曲线完成齿轮修形设计,修形结果表明齿轮传递误差进一步降低,并且采用二次曲线修形要好于直线修形,通过试验也验证了优化修形后的齿轮传动振动更小。本文研究表明:MASTA软件提供了很好的齿轮优化设计方法,以之为工具可展开展齿轮低噪声设计。
| [1] | 陈国钧, 曾凡明. 现代舰船轮机工程[M]. 长沙: 国防科技大学出社, 2001 : 312 -343. |
| [2] | 李润方, 王建军. 齿轮系统动力学-振动、冲击、噪声[M]. 北京: 科学出版社, 1997 : 421 -439. |
| [3] |
渠珍珍, 鲍和云, 朱如鹏. 高重合度行星齿轮系参数优化设计[J]. 机械设计与制造 , 2011 (12) :41–43.
QU Zhen-zhen, BAO He-yun, ZHU Ru-peng. Optimal design for parameter of high contact ratio planetary gears system[J]. Machinery Design & Manufacture , 2011 (12) :41–43. |
| [4] |
唐进元, 雷敦财. 基于Kisssoft软件的行星传动装置齿轮参数优化设计[J]. 机械传动 , 2010, 34 (12) :15–19.
TANG Jin-yuan, LEI Dun-cai. The parameter optimization design of planetary reducer based on Kisssoft software[J]. Journal of Mechanical Transmission , 2010, 34 (12) :15–19. |
| [5] |
汤鱼, 宿吉鹏, 王志强. 单级行星齿轮传动系统齿廓修形研究[J]. 舰船科学技术 , 2013, 35 (6) :23–27.
TANG Yu, SU Ji-peng, WANG Zhi-qiang. Research on tooth profile modification of planetary transmission base on transmission error[J]. Ship Dcience and Technology , 2013, 35 (6) :23–27. |
| [6] |
蒋进科, 方宗德, 王峰. 降低斜齿轮噪声的对角修形优化设计[J]. 振动与冲击 , 2014, 33 (7) :63–67.
JIANG Jin-ke, FANG Zong-de, WANG Feng. Optimal design with diagonal modification for reducing helical gear noise[J]. Journal of Vibration and Shock , 2014, 33 (7) :63–67. |
| [7] | LIU G, PARKER R G. Dynamic modeling and analysis of tooth profile modification for multimesh gear vibration[J]. Journal of Mechanical Design , 2008, 130 (12) :121402. DOI:10.1115/1.2976803 |
| [8] |
霍肇波, 徐振忠, 常山, 等. 降低斜齿轮噪声的齿轮修形优化设计[J]. 热能动力工程 , 1995, 10 (5) :334–341.
HUO Zhao-bo, XU Zhen-zhong, CHANG Shan, et al. Optimized design of tooth profile correction to reduce helical gear noise[J]. Journal of Engineering for Thermal Energy and Power , 1995, 10 (5) :334–341. |
 2016, Vol. 38
2016, Vol. 38
