水下滑翔机是一种利用净浮力和姿态角调节获得推进力的新型水下航行器。相比于传统水下航行器,水下滑翔机具有成本低、航程远、持续工作能力强等优点。自1989年Henry Stommel首先提出“水下滑翔机”的概念以来[1],各式各样的水下滑翔机被研制出来并广泛应用于海洋探索之中。
传统水下滑翔机外形是由回转体壳体、水翼和操纵面组成。然而,回转体壳体外形不能像水翼一样提供非常高的升力,所以传统对回转体型的水下滑翔机即使在搭载了高展弦比水翼的情况下,其最大升阻比只能达到5左右[2],这严重影响了水下滑翔机的经济性。为了获得更高的水动力性能,2006年,美国海军研究办公室研制出了飞翼(Flying Wing)构形的水下滑翔机Xray[3]。飞翼构形是一种通过去除滑翔机的主体提高升阻比的外形布局。虽然这种构形显著地提高了滑翔机的最大升阻比,然而因为没有明显的主体,所以飞翼滑翔机的内部空间受到严重限制,无法安装更多的仪器和能源。
翼身融合(Blended-Wing-Body,简称BWB)布局的概念最早诞生于航空工业[4],使用翼身融合设计的飞机,有扁平且有翼剖面形状的机身,能产生一部分的升力。它的机翼与其他部位,则是平滑的与机身接合。这种构形即具有较高的升阻比,又有足够的内部空间,弥补了飞翼构形的缺点。
本文将翼身融合的概念应用到水下滑翔机的外形设计当中,设计一种小型翼身融合式水下滑翔机(50~70 kg),并用传统水下滑翔机Seaglider、扁平椭球壳体的水下滑翔机和翼身融合式水下滑翔机进行流体动力仿真,对结果进行分析对比。结果表明,相比于传统水下滑翔机,翼身融合水下滑翔机的水动力性能得到巨大提升。
1 外形设计 1.1 壳体形状的选取传统水下滑翔机一般采用回转体壳体,最常见的回转体壳体外形是带平行中段的水滴形(见图 1),如Slocum滑翔机[5]和Spray滑翔机[6],其优点是可获得较大的艇体容积。为了降低水下滑翔机的阻力从而提高升阻比,Huggins和Packwood提出[7]另一种壳体外形:低阻层流形壳体(见图 2),其优点在于通过形成合理的压力梯度,使得总长中大部分是层流段,从而阻力非常低,如Seaglider滑翔机[8]。然而,无论回转体壳体外形如何改进,都不能像水翼一样提供非常高的升力,所以传统对回转体型的水下滑翔机即使在搭载了高展弦比水翼的情况下,其最大升阻比只能达到5左右。2005年,Graver J G [9]设计了一种以扁平椭球体(见图 3)为壳体的水下滑翔机。文献[9]在内部容积相等的前提下,对回转体壳体和扁平椭球体壳体的水下滑翔机的水动力性能进行了初步对比研究,研究发现扁平椭球体壳体的水下滑翔机的升阻比要大于传统的回转体壳体的水下滑翔机。

|
图 1 壳体 Fig. 1 Body type 1 |

|
图 2 壳体 Fig. 2 Body type 2 |

|
图 3 壳体 Fig. 3 Body type 3 |
传统水下滑翔器的总体质量大约为50~70 kg左右。本文设计的翼身融合水下滑翔机总质量设定在60 kg左右。上述3种壳体的基本尺寸见表 1。
|
|
表 1 三种壳体的几何参数 Tab.1 Geometric parameters of three bodies |
从表 1可看出,在相同体积下,壳体3的浸湿表面积要小于壳体1和壳体2的浸湿表面积,这意味着壳体3相比于壳体1和壳体2具有较小的粘性阻力;壳体3在XOZ平面的投影面积要大于壳体1和壳体2在XOZ平面的投影面积,这意味着壳体3相比于壳体1和壳体2可以产生较大的升力。因此,为使设计出的翼身融合水下滑翔机具有较高的升阻比,本文采用扁平椭球体作为壳体的基本形状。
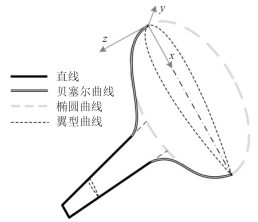
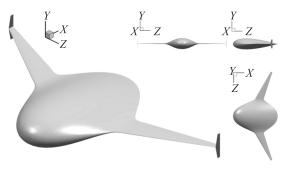
1.2 机翼与机身融合方式翼身融合布局的概念是指机身和机翼平滑的过渡融合,使滑翔机具有更好的流体动力性能。然而,扁平椭球体形的壳体很难与截面为NACA00系列翼型的机翼平滑地融合。而且,扁平椭球体壳体的弦向截面都是椭圆形,其流体动力性能不如NACA00系列翼型。因此,如图 4所示,本文并没有将扁平椭球体壳体与滑翔机机翼直接融合,而是先将扁平椭球体壳体与滑翔机机翼在ZOX平面的投影形状用3次贝塞尔曲线平滑地过渡融合,再将滑翔机的每个弦向截面都定义为NACA00系列翼型,且使翼型截面的厚度沿Z轴方向平滑过渡。本文设计的翼身融合水下滑翔机的三维模型如图 5所示。
|
图 4 翼身融合设计示意图 Fig. 4 Diagrammatic sketch of the BWB design |
|
图 5 翼身融合水下滑翔机三维模型 Fig. 5 The 3D model of the BWB underwater glider |
本文流体动力数值分析中所用的控制方程是不可压缩粘性流的Navier-Stokes方程,其主要包括连续性方程和动量方程[10],即
| $ \frac{\partial \rho }{\partial t}+\nabla \rho \vec{v}=0{\text{,}} $ | (1) |
| $ \frac{\partial }{\partial t}\left( \rho \vec{v} \right)+\nabla \left( \rho \vec{v}\vec{v} \right)=-\nabla p\text{+}\nabla \bar{\bar{\tau }}\text{+}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}{\text{。}} $ | (2) |
式中:v为速度矢量;ρ,p,
本文采用的湍流模型为剪切应力输运k-ω模型(简称SST k-ω模型),该模型综合了k-ω模型在近壁面计算的优点和k-ε模型在远场计算的优点,其适用范围更广。
湍流强度k方程和频率ω方程[11]如下:
| $ \frac{\partial \rho k}{\partial t}+\nabla \left( \rho kU \right)=\nabla \left[ \left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\nabla k \right]+{{P}_{k}}-{{b}_{k}}\rho k\omega {\text{,}} $ | (3) |
| $ \frac{\partial \rho \omega }{\partial t}\!+\!\nabla \left( \rho U\omega \right)\!=\!\nabla \left[ \left( \mu \!+\!\frac{{{\mu }_{t}}}{{{\sigma }_{\omega }}} \right)\nabla \omega \right]\!+\!a\frac{\omega }{k}{{P}_{k}}\!-\!{{b}_{\omega }}\rho {{\omega }^{2}}{\text{。}} $ | (4) |
式中:Pk为由层流速度梯度而产生的湍流动能,σk=2.0和σω=2.0分别为k方程和ω方程的湍流能量普朗克数;a=5/9为ω梯度产生的湍动能系数;bk=0.09和bω=0.075分别为k和ω扩散产生的湍动能系数;μt=ρk/ω为涡黏度。
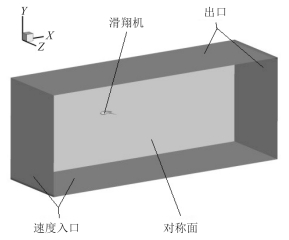
2.3 计算域和网格划分由于本研究只计算滑翔机在不同攻角下的流体动力且滑翔机左右对称,所以可以取其一半划分网格进行计算。如图 6所示,计算区域为长25 × ct m,宽15 × ct m,高20 × ct m(ct为滑翔机的中心弦长)的长方形区域。速度入口设在距滑翔机的前端10 × ct m处;压力出口设在在距滑翔机的尾端15 × ct m处。
|
图 6 计算域 Fig. 6 Computational domain |
计算域的边界条件设定如下:
1)入口设为inletvelocity边界类型,选择笛卡尔坐标系速度分量定义方式,具体速度分量随攻角α的变化而变化,但其合速度大小为0.35 m/s;
2)出口设为pressure outlet边界类型;
3)对称面设为symmetry边界类型;
4)滑翔机壁面设为无滑移壁面;
5)壁面设为自由滑移边界。
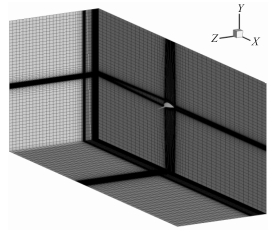
网格划分采用六面体结构化网格,数量在200万到250万之间。图 7展示了对称面的网格划分情况。如图 8所示,水下滑翔机壳体壁面处采用O网格进行加密,壁面第1层网格的y +值小于5。
|
图 7 结构化网格整体视图 Fig. 7 Grid structure in the computational domain |
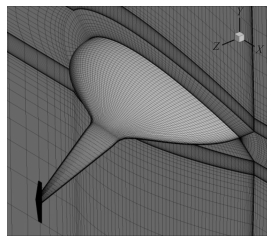
|
图 8 机身表面的结构化网格 Fig. 8 Detail of the boundary layers near the glider body |
为能更好地分析翼身融合水下滑翔机的水动力性能,本文对3种具有代表性的水下滑翔机模型进行了数值模拟。模型1(见图 9)为根据低阻层流回转体形水下滑翔机Seaglider的外形设计参数[12]生成的三维模型;模型2(见图 10)为扁平椭球体水下滑翔机;模型3(见图 11)为在模型2的基础上进行翼身融合设计的水下滑翔机三维模型。

|
图 9 模型1:Seaglider滑翔机 Fig. 9 Model 1: Seaglider underwater glider |

|
图 10 模型2:扁平椭球体水下滑翔机 Fig. 10 Model 2: underwater glider with a flat ellipsoid body |
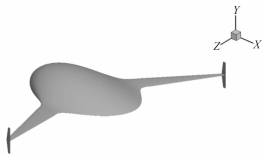
|
图 11 模型3:翼身融合式水下滑翔机 Fig. 11 Model 3: BWB underwater glider |
三种模型的主要几何参数见表 2。由表 2可知,模型1,模型2与模型3的排水量都在50~70 L之间,都属于小型水下滑翔机。其中,模型2采用扁平椭球体作为滑翔机的主体,所以在3种模型中具有最大的排水量和最小的浸湿表面积;模型3是在模型2的基本形状上进行翼身融合设计而得,其排水量略小于模型2且浸湿表面积略大于模型2;模型1作为传统回转体水下滑翔机Seaglider的三维模型,其排水量最小且浸湿表面积最大。
|
|
表 2 模型具体参数对照表 Tab.2 Parameters of specific models |
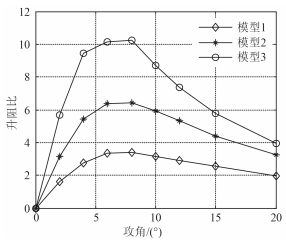
在航速0.35 m/s,攻角0°~20°的工况下,对3种模型进行CFD数值计算,将3种模型的阻力、升力和升阻比汇总并绘制成随攻角α的变化曲线图(见图 12~图 14)。
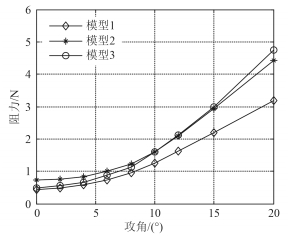
|
图 12 阻力随α的变化曲线 Fig. 12 Curves of drag changing with α |
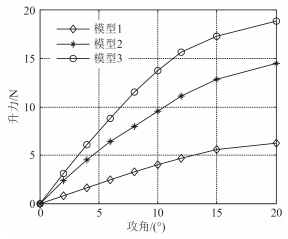
|
图 13 升力随α的变化曲线 Fig. 13 Curves of lift changing with α |
|
图 14 升阻比随α的变化曲线 Fig. 14 Curves of lift to drag ratio changing with α |
由图 12可知,在0°攻角下,模型1的阻力最小,模型3的阻力略大于模型1,而模型2的阻力明显大于模型1和模型3。3种模型的阻力都与攻角呈二次函数关系,其中,模型1随攻角的增大而增长的较慢,模型3随攻角的增大而增长的较快。由此可看出,模型1的低阻层流型外壳具有非常好的减阻特性;由于模型3相较于模型2进行了翼身融合设计,其0°攻角下的阻力要小于模型2,但阻力随攻角的增长速度快于模型2。
由图 13可知,3种模型均随攻角的增大而增大,在小攻角(0°~10°)下,升力与攻角程线性关系,当攻角大于10°时,升力随攻角的增长速度逐渐变慢。模型3和模型2由于采用扁平体壳体,其ZOX平面上的投影面积远大于模型1,因此,相同攻角下,模型3和模型2的升力远大于模型1的升力;模型3相较于模型2进行了翼身融合设计,ZOX平面上的投影面积进一步增大,因此,相同攻角下,模型3的升力大于模型2的升力。
由图 14可知,3种模型的升阻比随攻角的增大先增大后减小,且都在8°攻角附近达到最大升阻比,即3种模型都在8°攻角附近具有最大滑翔经济性。由于模型3既有较好的阻力特性又有良好的升力特性,所以模型3的升阻比远大于模型1与模型2。
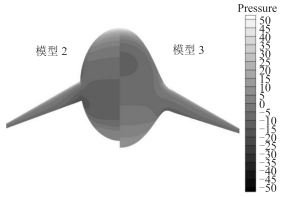
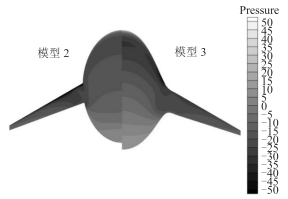
图 15和图 16分别为模型2与模型3的上、下表面的压力分布云图。从图中可看出,进行翼身融合设计的模型3的压力梯度分布比较均匀,而未进行翼身融合设计的模型2在机翼与壳体连接出压力集中却分布不均匀,这是导致模型3的阻力小于模型2的主要原因之一。
|
图 15 模型2和模型3下表面压力云图 Fig. 15 Pressure distributions of the lower surface |
|
图 16 模型2和模型3上表面压力云图 Fig. 16 Pressure distributions of the upper surface |
在水下滑翔机外形设计中,升阻比是衡量水下滑翔机水动力性能最重要的指标之一,除了尽量获得尽可能高的升阻比之外,尽量降低水动力对滑翔机OZ轴的俯仰力矩,可以增加水下滑翔机的航行稳定性。为了综合描述水下滑翔机的水动力性能,本文引用文献[13]中提出的水动力性能加权公式:
| $ \max \left\{ {{\omega _1}\frac{{{F_L}\left( \alpha \right)}}{{{F_D}\left( \alpha \right)}} + {\omega _2}\frac{1}{{{M_{pitch}}\left( \alpha \right)}}} \right\},{\omega _1} = 0.6,\;{\omega _2} = 0.4{\text{。}} $ | (5) |
式中:FL(α),FD(α)和Mpitch(α)分别为3种水下滑翔器在α攻角下受到的升力、阻力和最大俯仰力矩;ω1和ω2为加权系数。本文根据公式计算出3种水下滑翔机模型的水动力性能如表 3所示。
|
|
表 3 水动力性能对照表 Tab.3 The hydraulic performance comparison of specific models |
由表 3可知,模型3的加权值最高,即具有翼身融合外形的模型3的水动力性能要远远好于模型1和模型2。以上数据表明,翼身融合水下滑翔机在航行过程中具有更高的工作效率。
4 结语本文将航空航天领域先进的翼身融合布局引入水下滑翔机的外形设计当中,对翼身融合水下滑翔机进行了初步的外形设计与水动力性能分析。结果表明,翼身融合布局极大地改善了水下滑翔机的水动力性能。本文的研究成果主要有:
1)扁平椭球体壳体相比与传统的细长回转体壳体具有较大的容积和较小的浸湿表面积,其更适合作为翼身融合水下滑翔机机身的基本形状;
2)扁平椭球体型的水下滑翔机的水动力性能高于传统水下滑翔机;
3)扁平椭球体型的水下滑翔机在进行翼身融合设计之后,其压力分布得到极大改善,水动力性能进一步提高。翼身融合水下滑翔机的阻力、升力和升阻比随攻角的变化趋势与传统滑翔机基本一致,并且翼身融合水下滑翔机的水动力性能远远高于传统水下滑翔机。
| [1] | STOMMEL H. The Slocum mission[J]. Oceanography , 1989, 2 (1) :22–25. DOI:10.5670/oceanog |
| [2] | 李志伟, 崔维成. 水下滑翔机水动力外形研究综述[J]. 船舶力学 , 2012, 16 (7) :829–837. |
| [3] | ONR. Liberdade XRay advanced underwater glider[EB/OL]. http://www.onr.navy.mil/media/extra/fact_sheets/advanced_underwater_glider.pdf. |
| [4] | 朱自强, 王晓璐, 吴宗成, 等. 民机的一种新型布局形式-翼身融合体飞机[J]. 航空学报 , 2008, 29 (1) :49–59. |
| [5] | WEBB D C, SIMONETTI P J, JONES C P. SLOCUM:an underwater glider propelled by environmental energy[J]. IEEE Journal of Oceanic Engineering , 2001, 26 (4) :447–452. DOI:10.1109/48.972077 |
| [6] | SHERMAN J, DAVIS R E, OWENS W B, et al. The autonomous underwater glider "Spray"[J]. IEEE Journal of Oceanic Engineering , 2001, 26 (4) :437–446. DOI:10.1109/48.972076 |
| [7] | HUGGINS A, PACKWOOD A R. Wind tunnel experiments on a fully appended laminar flow submersible for oceanographic survey[J]. Ocean Engineering , 1995, 22 (2) :207–221. DOI:10.1016/0029-8018(94)00005-0 |
| [8] | ERIKSEN C C, OSSE T J, LIGHT R D, et al. Seaglider:a long-range autonomous underwater vehicle for oceanographic research[J]. IEEE Journal of Oceanic Engineering , 2001, 26 (4) :424–436. DOI:10.1109/48.972073 |
| [9] | GRAVER J G. Underwater gliders:dynamics, control and design[D]. Princeton:Princeton University, 2005. http://www.researchgate.net/publication/35214965_Underwater_gliders_dynamics_control_and_design_ |
| [10] | 景思睿, 张鸣远. 流体力学[M]. 西安: 西安交通大学出版社, 2001 : 91 -96. |
| [11] | 胡志强, 林扬, 谷海涛. 水下机器人粘性类水动力数值计算方法研究[J]. 机器人 , 2007, 29 (2) :145–150. |
| [12] | RUDNICK D L, DAVIS R E, ERIKSEN C C, et al. Underwater gliders for ocean research[J]. Marine Technology Society Journal , 2004, 38 (2) :73–84. DOI:10.4031/002533204787522703 |
| [13] | 谷海涛, 林扬, 胡志强, 等. 基于代理模型的水下滑翔机机翼设计优化方法[J]. 机械工程学报 , 2009, 45 (12) :7–14. |
 2016, Vol. 38
2016, Vol. 38
