2. 重庆交通大学 航运与船舶工程学院, 重庆 400074
2. Shipping and Marine Engineering College, Chongqing Jiaotong University, Chongqing 400074, China
随着国际航运事业的发展,人们对于船舶码头的需求量正在不断增大,随着开敞式和半开敞式码头的增多[1],码头系泊船舶所处的自然环境越来越恶劣,因此对码头系泊船舶的研究正日益受到科研人员的关注,为了保证船舶的系泊安全和货物的正常装卸,对其进行水动力性能分析是很有必要的[2, 3]。
码头系泊是一个复杂、非线性和多重耦合的系统,由码头、船舶、护舷和系泊缆组成。对其进行研究主要集中在船舶的运动响应和系泊缆张力2个方面[4, 5]。在运动响应研究方面,徐兆全[6]通过总结试验和对比分析得出,在风浪流的联合作用下,船体6个自由度的运动响应在不同海况、不同装载吃水等条件下表现出不同的运动特性;天津大学发表的研究[7]表明,船舶的运动存在着许多非线性现象,在实际问题的研究过程中不能忽略。在系泊缆张力研究方面,刘必劲[8]研究了在波浪作用下,大型开敞式码头系泊船舶的系泊缆受力情况,并总结了系泊缆张力计算公式。刘宇[9]重点研究了波浪周期对码头系泊船舶的影响,提出当风浪流条件比较恶劣时,应当随时调整缆绳数量,从而保证系泊安全。
目前对于码头系泊问题的研究,大部分都是通过模型试验的方式,进行数值仿真研究的相对较少[10-11]。本文利用Ansys-AQWA软件,基于三维势流理论,对船舶的水动力性能和系泊形式进行研究,沿型深方向对系泊缆进行优化,为码头系泊船舶系泊方式的优化提供新的思路。
1 环境载荷的计算 1.1 风载荷根据OCIMF(Oil Companies International Marine Forum)规范的有关规定,船舶受到的纵荡方向风力Fxw、横荡方向风力Fyw和首摇风力矩Mxyw分别为:
| $ {{F}_{xw}}=\frac{1}{2}{{C}_{xw}}{{\rho }_{w}}V_{w}^{2}{{A}_{T}}{\text{,}} $ | (1) |
| $ {{F}_{yw}}=\frac{1}{2}{{C}_{yw}}{{\rho }_{w}}V_{w}^{2}{{A}_{L}}{\text{,}} $ | (2) |
| $ {{M}_{xyw}}=\frac{1}{2}{{C}_{xyw}}{{\rho }_{w}}V_{w}^{2}{{A}_{L}}{{L}_{BP}}{\text{。}} $ | (3) |
式中:系数Cxw、Cyw和Cxyw,可根据不同的吃水情况(满载或者是压载)、不同的角度和不同的船型进行选取;ρw为空气密度;Vw为风速;AT为船舶的横向受风面积;AL为船舶的纵向受风面积;LBP为船舶的垂线间长。
1.2 流载荷根据OCIMF(Oil Companies International Marine Forum)规范的有关规定,船舶受到的纵荡方向流力Fxc、横荡方向流力Fyc和首摇流力矩Mxyc分别为:
| $ {{F}_{xc}}=\frac{1}{2}{{C}_{xc}}{{\rho }_{c}}V_{c}^{2}{{L}_{BP}}T{\text{,}} $ | (4) |
| $ {{F}_{yc}}=\frac{1}{2}{{C}_{yc}}{{\rho }_{c}}V_{c}^{2}{{L}_{BP}}T{\text{,}} $ | (5) |
| $ {{M}_{xyc}}=\frac{1}{2}{{C}_{xyc}}{{\rho }_{c}}V_{c}^{2}L_{BP}^{2}T{\text{。}} $ | (6) |
式中:系数Cxc,Cyc和Cxyc可根据不同的水深和吃水比、不同的角度、不同的吃水情况和不同的船型进行选取;ρc为海水密度;Vc为流速;LBP为垂线间长;T为吃水。
1.3 系缆力系泊缆绳的弹性拉伸一般具有非线性规律,威尔逊提出系泊缆拉伸应力与变形间的关系式如下:
| $ {{F}_{R}}={{K}_{c}}{{d}^{2}}{{\left( \frac{\Delta S}{S} \right)}^{n}}{\text{。}} $ | (7) |
式中:FR为缆绳拉力,kN;d为缆绳直径,m;Kc为缆绳弹性常数,对尼龙缆,Kc=1.56 × 104 MPa,对丝缆,Kc=2.75 × 105 MPa;n为与材特性有关的指数,对尼龙缆n=3,对钢丝缆n=1.5;ΔS/S为缆绳相对伸长。
如果带缆桩的坐标为(X1, Y1, Z1),船舶在初始船位时导缆孔的坐标(X2, Y2, Z2),缆绳原长可由下式确定:
| $ S=\sqrt{{{\left( {{X}_{2}}-{{X}_{1}} \right)}^{2}}+{{\left( {{Y}_{2}}-{{Y}_{1}} \right)}^{2}}+{{\left( {{Z}_{2}}-{{Z}_{1}} \right)}^{2}}}{\text{,}} $ | (8) |
如果自由度变化后船舶移动到某一位置,导缆孔的坐标变为(X'2, Y'2, Z'2),缆绳长度相应变为:
| $ {{S}^{'}}=\sqrt{{{\left( X_{2}^{'}-{{X}_{1}} \right)}^{2}}+{{\left( Y_{2}^{'}-{{Y}_{1}} \right)}^{2}}+{{\left( Z_{2}^{'}-{{Z}_{1}} \right)}^{2}}}{\text{,}} $ | (9) |
其中(X'2, Y'2, Z'2)由下式确定:
| $ \left\{ \begin{matrix} X_{2}^{'}={{I}_{x}}+\cos \theta \times {{X}_{2}}-\sin \theta \times {{Y}_{2}} {\text{,}} \\ Y_{2}^{'}={{I}_{y}}+\sin \theta \times {{X}_{2}}+\cos \theta \times {{Y}_{2}} {\text{,}} \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!Z_{2}^{'}=Z {\text{。}} \\ \end{matrix} \right. $ | (10) |
式中:Ix为沿X轴的位移;Iy为沿Y轴的位移;θ为相对于X轴的转角。
2 码头系泊船舶水动力频域分析本文以Ansys软件建立有限元模型,目标船舶的长宽比为6:1,排水量为30 000 t。通过AQWA-LINE模块,对船舶进行频域水动力性能分析,选取计算水深20 m为研究对象。由于模型沿X轴左右对称,在计算的过程中,采用的浪向角为0°,-30°,-60°,-90°,-120°,-150°和-180°。
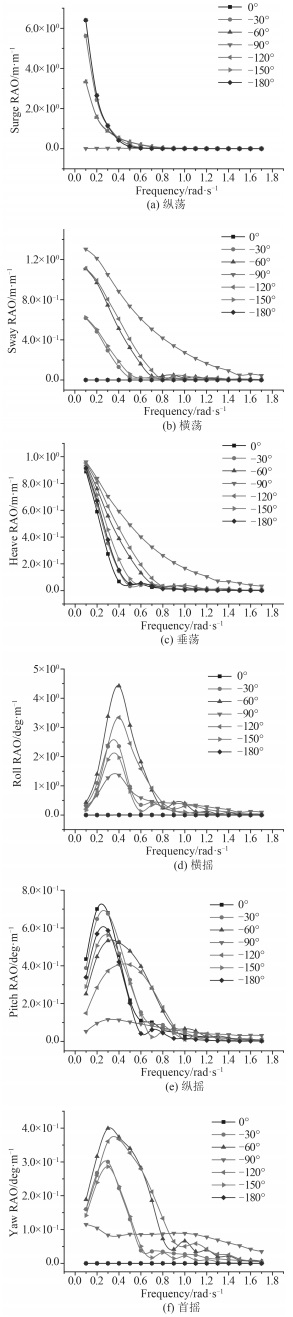
从图 1中可看出,纵荡、横荡和垂荡的RAO随着频率的增加都呈下降趋势;当入射角为0°~-90°时,纵荡RAO随着入射角的增大而减小,横荡和垂荡RAO随着入射角的增大而增大,当入射角为-90°~-180°时,变化规律正好相反。
|
图 1 运动响应幅值算子随浪向角变化曲线 Fig. 1 RAO in different wave directions |
横摇、纵摇和首摇3个旋转自由度上的RAO随着频率的增加都是先增大后减小的过程,与纵荡、横荡和垂荡方向上的RAO类似,当频率小于0.8 rad/s时,运动响应幅值算子随频率的波动较大,且有峰值出现,当频率大于0.8 rad/s时,随频率基本不变且接近于0。
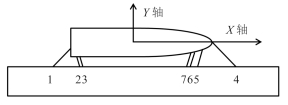
3 码头系泊船舶时域耦合分析在进行时域耦合分析时,设置7个护舷,每隔8 m设置1个,编号为No.1~No.7,护舷采用的是SUC2250H标准鼓型橡胶护舷,它的设计压缩变形量是52.5%,设计反力是2 502 kN,设计吸能为2 472 kJ,其最大压缩变形量是55%,最大反力是2 659 kN,最大吸能为2 617 kJ。系泊缆的材料为超高分子量聚乙烯,直径为40 mm,破断载荷为1 086 kN。船上的导缆孔的位置坐标和码头上的系泊点坐标见表 1。缆绳编号与船和码头的相对位置如图 2所示。在本次模拟中采用的环境条件如表 2所示。
|
|
表 1 系泊点坐标 Tab.1 Coordinates of mooring points |
|
图 2 码头系泊示意图 Fig. 2 Mooring at the dock |
|
|
表 2 环境条件 Tab.2 Environmental conditions |
为了研究船上系泊点的位置沿型深方向变化对船舶水动力响应的影响,在原有系泊方式的基础之上,又设计了2种系泊方式,但码头上的系泊点并没有变化,只是船上的系泊点有变化,如表 3所示。从表 3可看出,优化方案1在原有系泊方式的基础之上,提高系泊点的坐标,优化方案2在原有系泊方式的基础之上,降低系泊点的坐标,它们的X值和Y值都没有变化,只有Z值发生改变。
|
|
表 3 沿型深方向优化方案坐标值 Tab.3 Coordinates of the optimized solutions along the depth direction |
表 4给出了不同系泊方式下,船舶重心处6个自由度上的运动响应的统计特性。Higher表示优化方案1的结果,Original表示原有系泊方式的结果,Lower表示优化方案2的结果。
|
|
表 4 运动响应统计特性 Tab.4 Characteristics of motion response |
从表 4中可看出,系泊方式沿型深方向的优化,对船舶的垂荡和纵摇的影响不大,对纵荡、横荡、横摇和首摇的影响较大;系泊方式的升高,会使船舶的运动响应增大,而系泊方式的降低,会使船舶的运动响应变小。以纵荡为例,当系泊方式升高时,船舶偏离原始重心位置最远,为-7.379 m,当系泊方式降低时,船舶偏离原始重心位置最近,为-5.406 m,原始系泊方案中船舶偏离原始重心位置为-6.101 m。
3.1.2 沿型深方向优化系泊缆张力分析沿型深方向系泊方式的变化,不仅对船舶运动响应产生影响,对系泊缆张力也会产生影响,表 5给出了7个系泊缆张力最大值的统计特性。
|
|
表 5 系泊缆张力统计特性 Tab.5 Characteristics of tension of mooring line |
从表 5中可以看出,系泊方式沿型深方向的优化对船舶系泊缆张力的影响比较大。系泊方式的升高,在一定程度上会使系泊缆张力减小,会使系泊缆张力的分布更加的均匀,而系泊方式的降低,在一定程度上会使系泊缆张力升高,会使系泊缆张力的分布更加的分散。以3号系泊缆为例,系泊方式的升高使系泊缆张力与原来相比减小了9.37%,而系泊方式的降低使系泊缆张力与原来相比增加了1.13%。
为了更加形象地反映系泊方式沿型深方向的优化对船舶系缆力的影响,图 3给出了3号系泊缆在不同系泊方式下的受力情况,从图中可以看出,3号系泊缆有效张力随着船上系泊点的升高而减小。

|
图 3 3号系泊缆有效张力时历曲线 Fig. 3 Time history of tension of mooring line 3 |
从前面的计算中可以发现,在风浪流的作用下,2号和3号系泊缆的受力相对较大,即尾横缆受力大,为了减小其受力,需要对其进行优化设计。本文的优化思路是增加尾横缆的长度,因为缆绳变长之后,弹性增加,能有效地减小缆绳受力。所以在进行优化设计时,将码头上的尾横缆系泊点在原来的基础之上,沿船宽方向向后移动2 m,4 m和6 m,其余系泊缆的系泊方式不变。
3.2.1 尾横缆优化运动响应分析表 6给出了不同系泊方式下,船舶重心处6个自由度上的运动响应的统计特性。Original表示原有系泊方式的结果,Change1表示尾横缆后移2 m的结果,Change2表示尾横缆后移4 m的结果,Change3表示尾横缆后移6 m的结果。
|
|
表 6 运动响应统计特性 Tab.6 Characteristics of motion response |
从表中可以看出,尾横缆的优化对船舶的垂荡、横摇、纵摇的影响比较小,但是对船舶的纵荡和横荡的影响比较大。从纵荡和横荡方向上看,随着尾横缆的后移,船舶的运动响应在不断增大,但从首摇方向上看,随着尾横缆的后移,其会不断减小。以纵荡方向为例,原始的系泊方式偏离原始重心位置最远处的坐标为-6.101 m,横缆后移2 m后的系泊方式偏离原始重心位置最远处的坐标为-6.492 m,横缆后移4 m后的系泊方式偏离原始重心位置最远处的坐标为-6.914 m,横缆后移2 m后的系泊方式偏离原始重心位置最远处的坐标为-7.328 m。
3.2.2 尾横缆优化系泊缆张力分析对尾横缆进行优化设计,不仅对船舶运动响应产生影响,而且对系泊缆张力也会产生影响,表 7给出了7个系泊缆张力最大值的统计特性。
|
|
表 7 系泊缆张力统计特性 Tab.7 Characteristics of tension of mooring line |
从表 7中可以看出,尾横缆优化对船舶系泊缆张力的影响比较大。随着尾横缆的后移,在一定程度上会使尾横缆张力逐渐减小,会使系泊缆张力的分布更加的均匀。根据3.2.1中的结论,尾横缆的后移会使船舶的运动响应变大,所以虽然在一定范围内,尾横缆的后移会使尾横缆的受力减小,但由于运动响应增大,所以也不能无条件地将尾横缆后移。以3号系泊缆为例,将尾横缆后移2 m与原始系泊方式相比,尾横缆受力减小了5.69%,将尾横缆后移4 m与原始系泊方式相比,尾横缆受力减小了11.12%,将尾横缆后移6 m与原始系泊方式相比,尾横缆受力减小了15.39%。
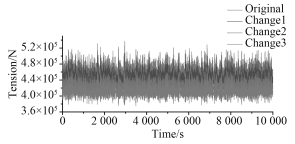
为了更加形象地反映系泊方式尾横缆的优化对船舶系缆力的影响,图 4给出了3号系泊缆在4种尾横缆布置方式情况下的受力情况,从中可以更加直观地看到,随着尾横缆的后移,3号系泊缆所受张力在逐渐减小。
|
图 4 3号系泊缆有效张力时历曲线 Fig. 4 Time history of tension of mooring line 3 |
水动力性能是船舶的重要内容之一。本文应用Ansys-AQWA软件,对码头系泊船舶进行耦合动力响应分析,其主要结论如下:
1)从不同浪向角对船舶频域水动力性能影响中可以看出,纵荡、横荡和垂荡3个位移自由度上的RAO随着频率的增加都呈下降趋势,横摇、纵摇和首摇3个旋转自由度上的RAO随着频率的增加都是先增大后减小的过程,有峰值出现。
2)沿型深方向优化结果表明,系泊方式沿型深方向的优化,对船舶的垂荡和纵摇的影响不大,对纵荡、横荡、横摇和首摇的影响较大;系泊方式的升高,会使船舶的运动响应增大,但在一定程度上会使系泊缆张力减小,会使系泊缆张力的分布更加均匀;而系泊方式的降低,会使船舶的运动响应变小,在一定程度上会使系泊缆张力升高,会使系泊缆张力的分布更加分散。沿型深方向对系泊缆布置方式进行优化以及优化的结果,为码头系泊船舶系泊方式的优化提供了新的思路。
3)尾横缆优化结果表明,随着尾横缆的后移,在一定程度上会使尾横缆张力逐渐减小,会使系泊缆张力的分布更加均匀,但会使船舶的纵荡和横荡方向上的运动响应变大。
| [1] |
黎泉.马迹山港区卸船码头系泊安全研究[D].大连:大连海事大学, 2012.
LI Quan. Study on the safety of mooring of Majishan port[D]. Dalian:Dalian Maritime University, 2012. http://cdmd.cnki.com.cn/article/cdmd-10151-1012345434.htm |
| [2] |
宋向群, 刘宇, 唐国磊. 系泊索属性对开敞式码头船舶系泊安全的影响分析[J]. 港工技术 , 2010, 47 (6) :18–20.
SONG Xiang-qun, LIU Yu, TANG Guo-lei. Analysis of mooring cable property influence on ship mooring safety of open terminal[J]. Port Engineering Technology , 2010, 47 (6) :18–20. |
| [3] |
张健, 连建鲁, 杨勇, 等. 缆绳预张力和刚度对自升式平台码头系泊性能的影响[J]. 舰船科学技术 , 2015, 37 (11) :39–43.
ZHANG Jian, LIAN Jian-lu, YANG Yong, et al. The influence of mooring line's pretension and stiffness on the performance of jack up platform quay mooring system[J]. Ship Science and Technology , 2015, 37 (11) :39–43. |
| [4] |
周丰, 张志明, 杨国平, 等. 码头系泊船舶系缆力及运动量数值模拟[J]. 中国港湾建设 , 2010 (S1) :60–63.
ZHOU Feng, ZHANG Zhi-ming, YANG Guo-ping, et al. Numerical simulation on the mooring line forces and movements of a moored ship[J]. China Harbour Engineering , 2010 (S1) :60–63. |
| [5] |
徐庭留, 朱克强, 周江华, 等. 大型船舶系泊系统的动力响应研究[J]. 港工技术 , 2012, 49 (1) :4–6.
XU Ting-liu, ZHU Ke-qiang, ZHOU Jiang-hua, et al. Dynamic response research of mooring system for large-scale vessels[J]. Port Engineering Technology , 2012, 49 (1) :4–6. |
| [6] |
徐兆全.浪流作用下系泊船舶运动及缆绳布局优化[D].大连:大连理工大学, 2007.
XU Zhao-quan. Berthing ships' movement and arrangement optimization of mooring lines in wave and current[D]. Dalian:Dalian University of Technology, 2007. http://cdmd.cnki.com.cn/article/cdmd-10141-2007210710.htm |
| [7] |
刘利琴, 唐友刚, 李红霞. 船舶运动的复杂动力特性在我国的研究进展[J]. 武汉理工大学学报(交通科学与工程版) , 2006, 30 (1) :183–186.
LIU Li-qin, TANG You-gang, LI Hong-xia. Study on dynamic behavior of ships motion in China[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering) , 2006, 30 (1) :183–186. |
| [8] |
刘必劲, 张亦飞, 徐伟. 波浪作用下大型开敞式码头系泊船舶系缆力研究[J]. 中国水运 , 2010, 10 (11) :5–7.
LIU Bi-jin, ZHANG Yi-fei, XU Wei. Study on the ship's mooring force at the open dock under the action of the waves[J]. China Water Transport , 2010, 10 (11) :5–7. |
| [9] |
刘宇, 唐国磊. 波浪周期对开敞式码头系泊安全影响研究[J]. 中国水运 , 2010, 10 (8) :30–31.
LIU Yu, TANG Guo-lei. Study on the wave period's effect to mooring safety at the open dock[J]. China Water Transport , 2010, 10 (8) :30–31. |
| [10] |
信书.码头前系泊船舶运动响应的数值模拟[D].大连:大连理工大学, 2005.
XIN Shu. Numerical simulation on hydrodynamic response of berthing ships[D]. Dalian:Dalian University of Technology, 2005. |
| [11] |
吴小鹏.深海半潜式钻井平台码头系泊系统数值计算与模型试验研究[D].上海:上海交通大学, 2010.
WU Xiao-peng. Numerical calculation and model test study on a quay mooring deep water semi-submersible drilling platform[D]. Shanghai:Shanghai Jiao tong University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10248-2010204012.htm |
 2016, Vol. 38
2016, Vol. 38
