2. 集美大学 轮机工程学院, 福建 厦门 361021
2. School of Marine Engineering, Jimei University, Xiamen 361021, China
流固耦合法(FSI)主要研究两相介质间的相互作用,其在航空航天、水利、建筑、海洋、生物等领域都有重要应用[1]。在船舶领域,FSI被作为一种结构强度的计算手段,该法主要基于数值水池技术[2],该技术已被证明能够细致描述周围流场,最终获得与试验数据较吻合的结果[2]。
复合材料因其在减重、耐腐蚀性、强度方面的卓越性能被认为在造船领域有巨大的发展潜力,在船舶领域复合材料结构多以夹层板三明治结构呈现,主要包括轻质芯材、面板以及加强结构。复合材料双体艇作为一种新艇型,具有重量轻、稳性好、甲板面积大等优点,但其夹层材料、复杂的结构却给强度计算带来了挑战。目前,国内针对其强度计算主要采用规范公式法,FEM作为计算商船强度的最有效方法[3],在复合材料多体船艇计算领域还未完全普及,鲜有采用FSI计算的例子。国外应用FSI计算复合材料双体艇的例子[4]对结构进行了大量简化并且仅计算了顶浪航行工况,未考虑更易造成结构破坏的斜浪航行工况。鉴于目前复合材料双体艇的FEM主要参照钢质双体船计算指南[5],基于数值水池的FSI计算结果可以一定程度上对同工况下的FEM进行检验。
本文采用FSI对1艘52 ft复合材料双体艇进行顶浪、斜浪工况下结构的时域响应计算,将流体域模型与有限元详细模型分开建立,借助WORKBENCH耦合求解器进行求解。将结果与同工况下的FEM对比,重点关注前10大等效应力与主要结构最大、小主应力,所得结论为进一步丰富和细化针对复合材质双体船的结构数值计算提供了重要参考。
1 材料参数及结构模型主要参数包括面板/芯材材料特性,厚度以及铺层设置,面板材料必须要有足够的强度承受波浪外载荷,芯材则具有较低的密度以达到减轻整个游艇重量的目的,文中的艇体面板采用强度较高的E-玻璃纤维正交布、玻璃纤维短切毡、树脂交替铺设的结构形式,芯材为密度100 kg/m3 PVC泡沫。主要力学性能如表 1所示,面板数据为实测数据(试验样板见图 1)。
|
|
表 1 材料的力学参数列表 Tab.1 Properties of FRP panels and PVC Foam |

|
图 1 试验样板图 Fig. 1 Standard panels for testing |
艇体的有限元材料模型由上下面板、芯材的“三明治”形式模拟,泡沫芯材看成各向同性材料,面板层定义为各向异性材料。主尺度为:艇长15.83 m,设计水线长15.3 m,总型宽6.048 m,型深1.596 m,片体水线宽2.5 m,计算吃水0.78 m,排水体积16.6 t,片体中心距4.45 m。由于计算模型为薄壳结构,并且具有高柔中间层,较低的横向剪切刚度,在WORKBENCH中通过内插程序的方法选用SHELL181单元,划分网格后的模型如图 2所示。通过定义局部坐标系的方式,校正材料铺层方向使其符合实际情况。

|
图 2 网格模型 Fig. 2 Mesh model |
目前的数值造波方法主要有仿物理造波法和纯数值造波法两大类,由于仿物理造波需要运用动边界和动网格特性,大大增加了计算时间[6]。本文采用纯数值造波法中的边界造波法,所造波浪基于线性波浪理论[7],该理论假定波浪沿ox轴正向传播,模拟斜浪航行时,假定波浪的传播方向与游艇的航行方向ox轴正向成β角,波浪速度势经坐标转换后得到各方向的速度表达式
| $\left\{ \begin{align} & u={{C}_{0}}{{\xi }_{a}}\frac{\cosh (z+H)}{\sinh kH}\cdot \sin [k(x\cos \beta +y\sin \beta )-{{\omega }_{0}}t]\text{, } \\ & v=0\text{, } \\ & w={{C}_{0}}{{\xi }_{a}}\frac{\sinh (z+H)}{\sinh kH}\cdot \cos [k(x\cos \beta +y\sin \beta )-{{\omega }_{0}}t]. \\ \end{align} \right.$ | (1) |
式中:ξa为波幅;k为波数;H为水深;ω0为波浪的自然频率。系数C0表示为:
| ${{C}_{0}}=\frac{{{\omega }_{0}}}{k}=\sqrt{\frac{g}{k}\tanh kH}.$ | (2) |
本文采用人工阻尼消波的方法来消除所造波浪,其主要方法是模拟真实波浪水池的消波层,在消波区域的动量方程中直接添加阻尼项,通过控制外部给定的阻尼大小来实现消波,消波区位于流场尾域一个波长的范围。具体方法为加入UDF消波程序,给定计算工况下的波高、波长、波数等初始条件,完成对数值水池的模拟。
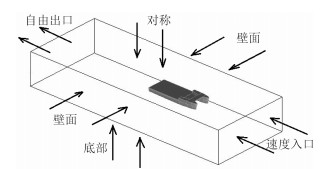
2.2 CFD模型通过对非耦合区域的简化建立流场分析模型,导入ICEM-CFD中划分网格并设置边界条件。本文将计算域定义为:纵向船首向前1倍船长,船尾向后2倍船长;横向左右舷侧各向两边延伸6倍片体型宽;竖向从水线处向下延伸10倍吃水,从水线处向上延伸5倍吃水。采用四面体网格为主的混合网格,总网格数为1889 795。边界条件设置如图 3所示,入口为速度入口,出口为自由出口,两侧及底面为滑移壁面,上表面为对称边界。
|
图 3 流场计算域示意图 Fig. 3 Fluid domain for hydrodynamic analysis |
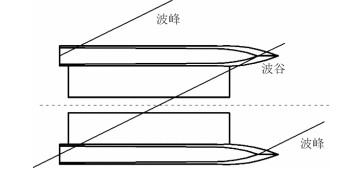
根据实际航行情况,本文选取顶浪(中拱与中垂)、斜浪工况为计算工况,设计航速13 kn。其中顶浪航行工况波长为艇水线长,斜浪工况波浪参数依据图 4发生片体不同步扭转选取,此时波长8.55 m,浪向角74°,波高取航行区域有义波高的均值0.8 m。为了模拟自由漂浮状态,采用惯性释放的边界条件。
|
图 4 斜浪航行工况简图 Fig. 4 Sketch of oblique waves |
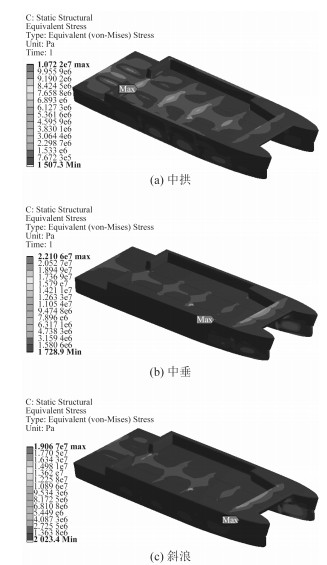
流固耦合计算的3种工况结果如图 5所示,中拱、中垂的结果显示,顶浪航行时除了产生总纵弯曲外,艇身还产生了小幅横向弯曲,主要原因是兴波向后传播过程中在两片体中间产生了回流、相互干扰造成片体两侧水压力分布不均。斜浪工况下左右片体应力分布并不对称,主要高应力区分布在右侧片体首部。此时,游艇两片体产生了不对称扭转,但由于波浪的抨击、上涌、破碎等作用,由此产生的艇体变形并不具有反对称性。
|
图 5 航行等效应力云图 Fig. 5 Equivalent stress nephogram for hogging |
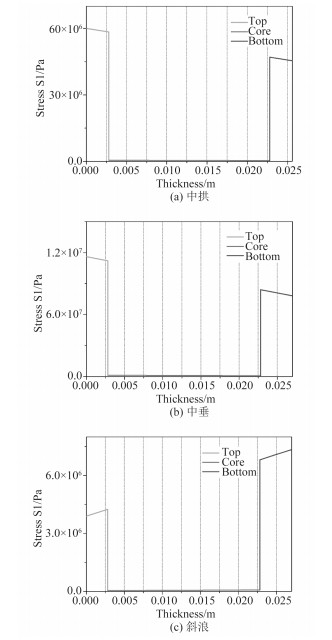
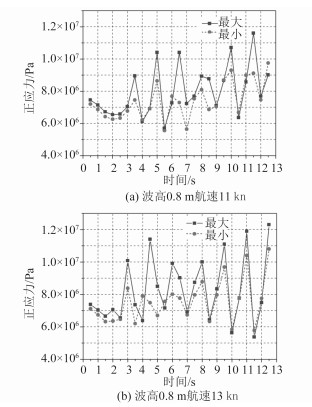
沿夹层板厚度纤维1方向的层间应力曲线如图 6所示,面板的主应力显著高于泡沫,说明夹层板结构面板主要承受拉压弯矩,而泡沫非承力结构,主要起支撑、提高夹层板刚度以抵抗变形作用。图 7为该艇在不同航速下(仅列出2种)的艇身结构最大、小主应力绝对值的时域响应图,选取航行时间区间6~12 s,从应力曲线的形状看,该波动呈现出了一定的周期性,该周期性紧随波浪周期变化但不吻合;此外,监测结果发现,最大最小正应力的发生位置并不一致,其曲线的变化趋势并不吻合;航速越大,最值主应力也越大。
|
图 6 工况纤维1方向层间应力曲线 Fig. 6 Normal stress distribution in1direction for Hogging |
|
图 7 全艇最大、小正应力的时域变化曲线图 Fig. 7 Dynamic response results of the whole ship's Max/Min. principle stress |
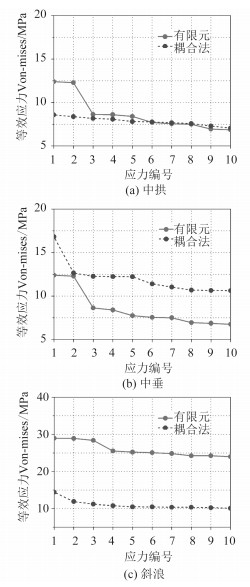
文中作为对照的FEM是参考CCS对于双体船的直接计算指南[5]完成,计算流程符合规范要求。为更好地考查FSI与FEM的结果,选取全艇具有代表性的前10大应力为对象比较3种工况的计算结果(见图 8)。由图可知,中拱状态下的前10大等效应力中,FEM前两大应力明显大于FSI,二者后8大应力吻合较好,FSI应力的波动幅度小于FEM;中垂工况下FSI计算的前10大应力值总体大于FEM,斜浪航行工况有限元法前10大等效应力值比FSI高出一倍,应力曲线走势相近。
|
图 8 FSI与FEA前10大等效应力曲线图 Fig. 8 Top 10 von-mises calculated by FSI/FEA for Hogging |
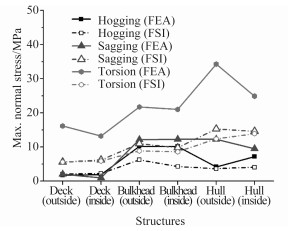
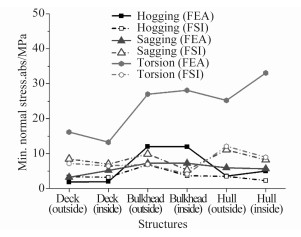
3种工况下主要结构最大、小主应力如图 9和图 10所示,FSI计算的3种工况最大、小主应力绝对值在15 MPa以下,数值上与FEM计算的中拱、中垂工况接近,斜浪工况FEM各主应力则显著大于FSI。中拱状态下FEM、FSI计算的最大、小主应力各结构变化趋势相似,根据主应力与变形形式的对应关系可知,中拱状态游艇的拉伸、压缩变形分布较均匀;中垂状态下全艇拉伸变形占主导;斜浪工况下FEM、FSI总体拉压变形均有分布,但注意到该工况主甲板、主艇体内外面板存在应力差,特别是直接受力的主艇体结构,内外面板应力差较大,可能造成夹层板发生层间破坏。
|
图 9 FSI与FEA最大主应力曲线图 Fig. 9 Max. principle stress of FSI/FEA |
|
图 10 FSI与FEA最小主应力曲线图 Fig. 10 Min. principle stress of FSI/FEA |
中拱状态下2种方法在主甲板内外面板、主艇体外面板的主应力极值基本吻合,曲线的走势相近,计算的全艇最值主应力均位于舱壁骨材;中垂状态下FSI在主甲板、主艇体的主应力均超过FEM,若考虑FEM的结果应具有一定的安全余量,则通过经验公式计算的中垂外载荷偏小;斜浪工况下FEM各结构最值主应力均显著高于FSI,曲线的基本走势相近,注意到FEM主艇体最大主应力显著高于主甲板和舱壁骨材,这是由FEM的计算载荷集中施加在主艇体底部所致。考虑到连接桥结构较片体更加脆弱,而斜浪工况造成的片体不同步扭转对连接桥结构威胁最大,主应力应具有一定的安全裕度。
4 结语本文采用流固耦合法对复合材料双体艇进行迎浪和斜浪航行工况下的结构响应计算,结果表明:
1)FSI顶浪工况下艇身结构除了产生总纵弯曲外,还有小幅横向弯曲,FSI的结果更接近于FEM组合工况。
2)夹层板面板主要承力,而泡沫芯材主要作用为提高刚度抵抗变形。
3)艇身结构最值主应力随着航速的升高而变大,其时域变化值呈现一定的周期性,并且最值主应力的发生位置也在不断变化,但变化周期并不与波浪周期完全吻合。
4)前10大等效应力与最值主应力曲线显示,中拱工况FEM与FSI吻合较好,此时艇体拉压变形分布较均匀;中垂工况FEM略小于FSI,全艇拉伸变形略占主导;斜浪工况FEM显著大于FSI,主应力曲线走势相比后者更陡。考虑到玻璃钢存在刚度小、建造工艺不确定等问题,在许用应力取0.3倍试验强度的基础上仍然需要留有一定的安全裕度。《钢质双体船直接计算指南》应用于文中的复合材料艇时,据其计算的中拱、中垂外载荷值偏小,若引入等强度的设计思想,可以取斜浪工况下FEM的平均安全系数作为修正系数。
| [1] |
钱若军, 董石麟, 袁行飞. 流固耦合理论研究进展[J]. 空间结构 , 2008, 14 (1) :3–15.
QIAN Ruo-jun, DONG Shi-lin, YUAN Xing-fei. Advances in research on fluid-structure interaction theory[J]. Spatial Structures , 2008, 14 (1) :3–15. |
| [2] |
赵艳, 朱仁庆, 刘珍. 三维数值波浪水池的构建和粘性影响的研究[J]. 舰船科学技术 , 2014, 36 (5) :42–48.
ZHAO Yan, ZHU Ren-qing, LIU Zhen. Simulation of 3D numerical wave tank and viscosity research[J]. Ship Science and Technology , 2014, 36 (5) :42–48. |
| [3] |
方昭昭, 赵丙乾, 朱仁传. 顶浪中船舶运动的数值模拟与波浪增阻计算[J]. 中国造船 , 2014, 55 (2) :8–17.
FANG Zhao-zhao, ZHAO Bing-qian, ZHU Ren-chuan. Numerical simulation of ship motion and calculation of added resistance in heading waves[J]. Shipbuilding of China , 2014, 55 (2) :8–17. |
| [4] |
牟宗宝, 林焰, 于雁云. 玻璃钢渔船帽形骨材顶角变化对应力集中的影响[J]. 船舶工程 , 2012, 34 (5) :17–19.
MU Zong-bao, LIN Yan, YU Yan-yun. Affect of angle change on stress concentration of cap-shape reinforcing rib in FRP fishing boat[J]. Ship Engineering , 2012, 34 (5) :17–19. |
| [5] | OJEDA R, PRUSTY B G, SALAS M. Finite element investigation on the static response of a composite catamaran under slamming loads[J]. Ocean Engineering , 2004, 31 (7) :901–929. DOI:10.1016/j.oceaneng.2003.08.008 |
| [6] | 中国船级社.海上高速船入级与建造规范[S].北京:人民交通出版社, 2012. |
| [7] | 李宏伟.数值水池造波方法研究[D].哈尔滨:哈尔滨工程大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10217-2010075206.htm |
| [8] |
方昭昭, 朱仁传, 缪国平. 数值波浪水池中航行船舶辐射问题的数值模拟[J]. 水动力学研究与进展 , 2011, 26 (1) :65–72.
FANG Zhao-zhao, ZHU Ren-chuan, MIAO Guo-ping. Numerical simulation on radiation problems of moving vessels in numerical wave tank[J]. Chinese Journal of Hydrodynamics , 2011, 26 (1) :65–72. |
 2016, Vol. 38
2016, Vol. 38
