2. 中国人民解放军91837部队, 浙江 舟山 316291 ;
3. 海军工程大学 电气工程学院, 湖北 武汉 430033
2. No.91837 Unit of the PLA, Zhoushan 316291, China ;
3. Electrical Engineering College Naval University of Engineering, Wuhan 430033, China
现代海战中军舰在使用过程中随时要面临作战,精确制导武器通常在舰体附近或舰体内部形成非接触爆炸,造成舰船结构及机械设备的破损,使舰船失去战斗力。在舰艇不沉没的情况下保持舰用设备的正常运转尤为显得重要,因此需要对其进行爆炸破坏分析。而要真实计算出舰用设备的冲击响应情况,就必须真实模拟出舰艇舱室的爆炸冲击环境。对结构抗爆的研究主要采用实验、理论分析与数值计算的方法。爆炸实验是检验结构抗爆性能最有效、最直接的方法,但由于是破坏性实验耗资巨大,难以承担试验开支。在爆炸冲击下,舱室结构要受到非周期性的瞬态作用以及考虑材料的塑性应变,这就使分析成为状态非线性和材料非线性组合在一起的高度非线性分析,在这种情况下使用理论分析的方法已经很难得到具体响应情况,必须借助于FEA(有限元分析)解决。
以往国内研究大多集中在舱室结构在不同爆炸冲击情况下的响应情况分析,侯海量等对舱内爆炸时冲击波的传播及板架结构的失效模式进行了分析;杜志鹏等对半穿甲内爆式反舰导弹攻击下舰船舷侧防护结构的响应与破损全过程进行了数值模拟仿真,并考虑了穿甲、爆炸破片和爆炸冲击波的耦合作用。但是关于舰艇设备在舱室爆炸条件下响应研究较少,对于舱室爆炸冲击与舱室内设备响应相结合的分析还未见报道[1-5]。
本文在建立含有大型设备的舱室结构有限元模型的基础上,利用瞬态分析软件LS_DYNA对其结构在空气域中的爆炸冲击响应进行了数值模拟。分析了爆炸冲击波在舱内的传播情况以及设备的响应情况,总结出了其中的规律,为提高舱室内设备的抗冲击能力提供一定的参考。
1 求解方法理论分析 1.1 爆炸冲击波传播用三维欧拉运动方程表达理想气体爆炸冲击波的传播:
| $\frac{\partial q}{\partial t}+\frac{\partial f(q)}{\partial x}+\frac{\partial g(q)}{\partial y}+\frac{\partial h(q)}{\partial z}=0$ | (1) |
式中:q为状态矢量;方程(1)满足质量、动量、能量守恒定律;f(q),g(q)和h(q)表示状态变量的流动,可写为:
| $\begin{align} & q=\left\{ \begin{matrix} \rho \\ \rho u \\ \rho v \\ \rho w \\ E \\ \end{matrix} \right\}\text{, }f(q)=\left\{ \begin{matrix} \rho u \\ \rho {{u}^{2}}+p \\ \rho uv \\ \rho uw \\ (E+p)u \\ \end{matrix} \right\}\text{, } \\ & g(q)=\left\{ \begin{matrix} \rho u \\ \rho uv \\ \rho {{v}^{2}}+p \\ \rho vw \\ (E+p)v\text{?}\!\!\neg\!\!\text{ } \\ \end{matrix} \right\}\text{, }h(q)=\left\{ \begin{matrix} \rho w \\ \rho uw \\ \rho vw \\ \rho {{w}^{2}}+p \\ (E+p)w \\ \end{matrix} \right\}. \\ \end{align}$ | (2) |
式中:ρ为材料密度;u,v,w为直角坐标系下3个速度分量;p为压力;E为气体总能量[6]。
1.2 流固耦合算法流固耦合算法是通过一定的约束方法将结构与流体耦合在一起,以实现力学参量的传递。耦合算法通过在两者之间定义耦合面,实现两者的耦合作用关系。耦合面既是欧拉网格与拉氏结构网格之间相互作用力的传递者,又是欧拉网格的流场边界。其算法的计算步骤为:
1)搜寻包含结构节点的流体单元,将结构的节点参数(质量、动量、节点力)分配给流体单元节点:
| $m(M, F)_{i}^{f}=m(M, F)_{i}^{f}+{{h}_{i}}\cdot m{{(M, F)}_{s}};$ | (3) |
2)计算新的流体节点加速度(速度):
| $a(v)_{i}^{f}=\frac{F(M)_{i}^{f}}{m_{i}^{f}}\text;$ | (4) |
3)约束结构节点的加速度(速度):
| $a{{(v)}_{s}}=\sum\limits_{i=1, 8}{{{h}_{i}}\cdot a(v)_{i}^{f}}.$ | (5) |
式中:m,M和F分别为节点质量、动量和节点力;a及v为节点加速度和速度;h为单个流体单元中包含的节点数;f和s为流体和实体单元符号[7]。
在本文的计算分析中,炸药及周围的空气介质采用欧拉网格进行描述,而舱室结构则采用拉格朗日网格进行描述。
2 建立有限元计算模型 2.1 材料状态方程舰艇舱室结构材料采用双线性弹塑性本构模型,材料的应变率效应由Cowper-Symonds模型描述,动态屈服强度:
| ${{\sigma }_{d}}=\left[{{\sigma }_{0}}+E\cdot {{E}_{h}}\cdot {{\varepsilon }_{p}}/(E-{{E}_{h}}) \right]\cdot \left[1+{{(\dot{\varepsilon }/D)}^{1/n}} \right].$ | (6) |
式中:σ0为静态屈服强度,E为弹性模量;Eh为应变硬化模量,εp为有效塑性应变;
计算中,假设舰艇结构的材料为低碳钢,对于低碳钢D=40.4 S-1,n=5,σ0=2.35×108 Pa,E=2.1×1011 Pa,γ=0.3,Eh=2.5×108 Pa,ρ=7 800 kg/m3,失效应变εf=0.28[8]。
炸药爆轰物的JWL状态方程:
| $p=A\left( 1-\frac{\omega }{{{R}_{1}}V} \right){{e}^{-{{R}_{1}}V}}+B\left( 1-\frac{\omega }{{{R}_{2}}V} \right){{e}^{-{{R}_{2}}V}}+\frac{\omega {{\rho }_{0}}e}{V}.$ | (7) |
式中:p为压力;A,B,ω,R1,R2为常数;V=ρ0/ρ,ρ0为初始密度,e为质量比内能。
计算中,炸药材料参数为ρ0=1630 kg/m3,A=5.574 8×1011 Pa,B=7.83×109 Pa,R1=4.5,R2=1.2,ω=0.34,e=4.969×106 J/kg,D=8 000 m/s。
假设空气介质为无粘性的理想气体,爆炸波的膨胀传播过程为绝热过程,空气的状态方程为:
| $p=(\gamma -1)\frac{\rho }{{{\rho }_{0}}}E\text.$ | (8) |
式中:p为空气压力,γ为绝热指数,ρ为空气密度,E为空气内能。计算中空气介质的状态参数为ρ0=1.29 kg/m3,γ=1.4,E0=2.5×105 Pa。
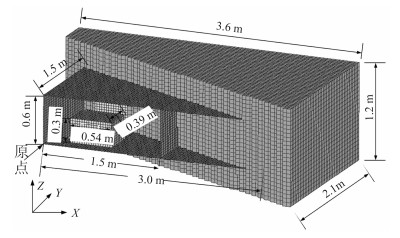
2.2 结构模型建立为了分析计算舱室内爆炸,需要建立包含设备的舱室有限元模型,限于计算机计算条件限制,建立的有限元模型为1:10的缩比模型。模型尺寸如图 1所示,最外层为空气,尺寸为3.6 m×1.2 m×2.1 m,单元基本尺寸为0.05 m,共划分六面体单元72 576个,节点78 477个;中间为舱室结构,共建立2个相邻舱室,尺寸都为3.0 m×1.5 m×0.6 m,用壳单元划分,初始板厚为0.005 m。舱室结构板架可以等效为平均板厚,假设矩形板架长为L,宽为B,板厚为D,其上有纵向骨架n根,骨架断面积为Fi,横向骨架m根,骨架断面积为Fj,则将板架中的骨架均布到板上,得到板架的相当板厚[9]:
|
图 1 舱室结构有限元模型 Fig. 1 FE model of cabin structure |
| $\bar{\delta }=(LB\delta +\sum\limits_{i=1}^{n}{{{F}_{i}}L+}\sum\limits_{j=1}^{n}{{{F}_{j}}B})/(LB)\text.$ | (9) |
舱室内部为2部设备的简化模型,用于研究舱室爆炸对其影响程度,其尺寸为0.54 m×0.39 m×0.3 m,用实体单元划分,单元尺寸为0.03 m,质量为5 000 kg。在空气网格的6个边界面上施加非反射边界条件,舱室约束施加在舱壁底部;舱室内设备不考虑其破坏效应,与舱室联为一体;炸药半径为0.04 m的球状TNT装药。用LS_DYNA瞬态分析软件对其爆炸冲击响应进行计算。
3 冲击仿真计算大型机械设备在舱室爆炸环境中的响应情况是本文研究的重点,爆炸冲击主要通过2种方式对舰载设备产生作用:一种是通过爆炸冲击波直接作用在设备的壳体上,这种作用主要形式是压力及冲量作用。舰艇舱室内有着许多机械设备,这些设备占用了很大一部分空间,这会使得舱室内爆炸冲击波传播与空的舱室爆炸传播相比更为复杂;另一种是通过冲击波对舱室结构的冲击,以加速度及位移的形式作用在设备基座上。
3.1 舱室内爆炸冲击波传播计算为研究爆炸冲击波在含设备舱室中的传播规律,对坐标为(0.1,0.1,0.5)为球心,半径为0.04 m的TNT装药爆炸进行0.04 s的数值计算。图 2是不同时刻舱室内XY剖面爆炸冲击波传播等值面图。从图中可以看出,冲击波首先从起爆点开始往外扩散(a);在0.007 s时绕过机电设备在对角处形成汇聚冲击波,其强度要大于入射冲击波(b);0.011 7 s时冲击波开始反向传播并分成2部分;一部分在设备表面形成反射冲击波,另一部分沿着舱壁向下传播(c);0.014 s时冲击波传播到舱室的2个角上,再一次形成了汇聚冲击波,而且右下角冲击波强度大于左上角(d);冲击波继续沿着舱壁继续传播,0.019 s时冲击波传播到设备与舱壁之间的狭小空间内,冲击波强度相对最大(e);0.025 s时沿着舱壁和设备表面传播的冲击波在2台设备之间汇合,并沿着上部设备继续向右上角传播(f);0.03 s时冲击波又传播到右上角形成汇聚冲击波,但经过衰减强度已经远不如当初(g);到了0.038 s,冲击波峰值区又一次转移到下部设备的周围(h)。再往后冲击波将按上述传播规律继续在舱室内来回传播,冲击波能量将逐渐衰减,直至结构内部流场平衡稳定。

|
图 2 不同时刻冲击波压力分布图 Fig. 2 Shock wave pressure distributing of different time |
从上述分析可看出,舱室内爆炸冲击波传播起初主要是放射状传播,直至碰到舱壁后形成反射或者在舱壁交接处形成汇聚,接下来冲击波传播沿着舱壁和设备表面进行传播。从图 2可看出,冲击波一般在舱室结构面交汇处或者几何空间出现突变的地方造成汇聚,从而造成局部冲击波压力增大,因此这些部位的结构需要进行加强,在这些位置放置设备也需特别注意。
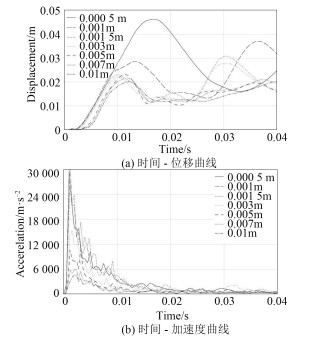
3.2 舱室内设备冲击响应计算舰船舱室由一定厚度的钢板焊接而成,不同厚度的钢板对于一定当量的炸药爆炸产生的变形,反射的冲击波压力都不同,因此有必要对舱室厚度对设备冲击响应的影响程度进行分析。本文选取舱壁厚度分别为0.000 5 m,0.001 m,0.001 5 m,0.003 m,0.005 m,0.007 m,0.01 m进行0.04 s仿真计算,得到舱室设备基座位移和基座加速度时间历程曲线结果如图 3所示。
|
图 3 不同舱壁厚度爆炸冲击响应计算结果 Fig. 3 Explosive shock response results of different cabin thickness |
从图 3(a)可以看到,随着舱壁厚度的增加,设备底部位移在逐渐减小。在0.000 5 m到0.001 5 m区间内,位移下降速度很快;但从0.001 5 m开始,底座的一次变形值虽然在减小但幅度很小,厚度在0.003 m以下时设备基座有较大的二次变形,从0.005 m开始二次变形幅度较小且3种厚度情况计算值基本相同。从曲线的形状来看,舱室结构没有发生大规模塑性变形,在第1波冲击波作用过后,舱壁回弹,但在第2波冲击波的作用下变形又开始增加,0.003 m以下厚度时,二次变形量甚至超过第1次变形值。从图 3(b)可看到,所有加速度曲线都呈现指数级递减,0.000 5 m,0.001 m和0.001 5 m曲线峰值基本相同,其余曲线峰值随厚度增加逐步递减。
从上述分析可看出,舱室内设备冲击响应无论是变形还是冲击加速度在舱壁厚度很薄时都很大,但当厚度增加到大于0.001 5 m时幅值都出现明显的降低。因此可以认为,舱壁厚度在达到一定厚度时能够明显减少爆炸冲击对设备的影响,对于减少底座变形,舱壁厚度应大于0.003 m,如果需要减小冲击加速度则厚度取值应根据具体设备的承受能力选择。另外舱壁厚度为0.000 5 m时,舱室被炸出直径约0.65 m破口;舱壁厚度为0.001 m时,舱室破口直径约为0.4 m。从图 3可以看出,无论是在位移曲线还是加速度曲线中,都没有因为舱室破口使得部分爆炸能量损失而影响设备的冲击响应,位移曲线中这2种情况设备变形仍然远大于其他情况,加速度曲线中前3种情况的响应峰值基本相同。因此可以得出结论,爆炸破口大小对舱室内设备的冲击响应结果影响程度有限,非特别需要不必考虑其影响。
4 结语基于以上计算分析,可以得出以下结论:
1)本文基于爆炸冲击波传播理论和流固耦合算法建立了含有大型设备的舱室简单有限元模型,并对模型进行了冲击波传播分析和舱室内设备冲击响应分析,通过分析得出了相关的结论。这些结论对改进舱室和设备结构,提高抗爆炸冲击能力有一定的参考价值。
2)冲击波在包含大型设备的舱室中传播情况比较复杂,但冲击波的高压区基本集中在舱壁交汇处或者设备附近,这对舱室内重要设备的安放提供了参考依据。
3)不同的舱壁厚度对舱室内设备的冲击响应有着较大影响,总的来说壁厚越大,对设备的冲击越小。但考虑到舰艇自身的重量限制,采用恰当厚度的舱壁能够较好地兼顾减轻设备的爆炸冲击破坏作用和舰艇的重量要求。
4)由于受到计算条件及试验条件的限制,本文进行的是定性计算分析,但依然能够得到一些对提高舱室抗爆炸能力有参考价值的结论。
| [1] | 戴佑斌, 周早生, 张尚根, 等. 爆炸冲击荷载作用下方舱的极限承载力计算与加固分析[J]. 振动与冲击 , 2006, 25 (3) :127–130. |
| [2] | 梅志远, 朱锡, 朱润泉. 船用加筋板架爆炸载荷下动态响应数值分析[J]. 爆炸与冲击 , 2004, 24 (1) :80–84. |
| [3] | KITAMURA O. Comparative study on collision resistance of side structure[J]. Marine Technology , 1998, 34 (4) :293–308. |
| [4] | CHUN S, KAPOOR H, KAPANIA R, et al. Nonlinear fluid-structure interaction of flexible shelters under blast loading[C]//Structures, Structural Dynamics, and Materials and Co-located Conference. Texas:ARC, 2005:18-21. |
| [5] | XIE W F, YOUNG Y L, LIU T G, et al. Dynamic response of deformable structures subjected to shock load and cavitation reload[J]. Computational Mechanics , 2007, 40 (4) :667–681. DOI:10.1007/s00466-006-0132-z |
| [6] | 杜志鹏, 李晓彬, 夏利娟, 等. 反舰导弹攻击舰船舷侧防护结构过程数值仿真[J]. 哈尔滨工程大学学报 , 2006, 27 (4) :484–487. |
| [7] | HALLQUIST J O. LS-DYNA keyword user's manual version 970[M]. California: LIVEMORE Software, 2003 : 716 -717. |
| [8] | 侯海量, 朱锡, 梅志远. 舱内爆炸载荷及舱室板架结构的失效模式分析[J]. 爆炸与冲击 , 2007, 27 (2) :151–158. |
| [9] | 朱锡, 白雪飞, 张振华. 空中接触爆炸作用下船体板架塑性动力响应及破口研究[J]. 中国造船 , 2004, 45 (2) :43–50. |
 2016, Vol. 38
2016, Vol. 38
