全垫升式气垫船是一种利用气垫将船体全部或大部分托离水面或地面的高速航行船舶,具有灵活、快速及负重强等特点,广泛应用于抗洪救灾、交通运输及登陆作战等多个领域[1]。以黄河凌汛防灾减灾需求为背景,相比于传统的爆炸破冰方式的局限性和安全性[2],使用气垫船破冰被认为是一种可靠、安全、高效及环保的新方法[3]。
气垫船破冰的机理可认为是移动载荷激励冰层引起的聚能共振增幅效应,当移动载荷以特定航速(临界速度)航行于冰面上时,可以激励冰层大幅变形,冰层内应力迅速提高,当其超过极限应力时冰层将破裂。Milinazzo[4]考察了矩形载荷长宽比对冰层响应的影响,得出了当载荷移动速度接近临界速度时冰层变形为无限大的结论。Mellor[5]提出了低速和高速2种气垫船破冰模式,并分析了适用条件。Takizawa[6]开展了移动载荷引起冰层变形的试验,发现存在使冰层下陷位移最大的临界速度。Squire[7-8]也得到了类似的实验结果,并总结了移动载荷激励冰层响应研究工作。胡明勇[9-11]计算了浮冰在脉冲、三角载荷及正弦载荷作用下的位移响应。刘巨斌[12-13]采用边界元与有限差分法对气垫船破冰进行了数值模拟。张志宏[14]利用薄膜开展了移动气垫载荷激励冰层变形相应的模型实验,证实了存在使薄膜下陷位移最大的载荷临界速度。卢再华[15-16]利用有限元方法对气垫船冰上航行过程进行了数值模拟并给出了临界航速的估算方法。
上述研究主要针对均匀水深无限大冰层情况,为研究河道岸壁对气垫船激励冰层响应的影响,采用动力学分析软件LS-DYNA,建立气垫船激励冰层位移响应的数值计算模型,针对不同载荷速度和岸壁宽度的冰层位移响应进行计算,分析不同载荷速度下冰层的位移响应及岸壁宽度对临界速度和冰层位移的影响,为进一步研究复杂边界条件下气垫船激励冰层响应提供基础。
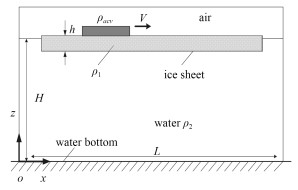
1 数值计算方法将气垫船等效为作用于冰层的气垫压力载荷,建立匀速移动载荷作用于浅水冰层的计算模型,认为冰层是各向同性、匀质、厚度均匀的弹性薄板,漂浮于水面,气垫在冰层上,与冰层接触,气垫上部为空气。气垫密度为ρacv,作用方向垂直向下,冰厚为h,冰密度为ρ1,水深为H,水密度为ρ2,如图 1所示。
|
图 1 计算模型 Fig. 1 Computational model |
采用兼顾拉格朗日和欧拉型有限元方法优点的任意拉格朗日-欧拉(ArbitraryLagrangian-Eulerian,ALE)方法进行计算,满足质量守恒、动量守恒和能量守恒。其基本控制方程如下:
| $\frac{\partial \rho }{\partial t}=-\rho \frac{\partial {{v}_{i}}}{\partial {{x}_{i}}}-{{w}_{i}}\frac{\partial \rho }{\partial {{x}_{i}}}, $ | (1) |
| $\rho \frac{\partial {{v}_{i}}}{\partial t}={{\sigma }_{ij, j}}+\rho {{b}_{i}}-\rho {{w}_{j}}\frac{\partial {{v}_{j}}}{\partial {{x}_{i}}}, $ | (2) |
| $\rho \frac{\partial e}{\partial t}={{\sigma }_{ij}}{{v}_{i, j}}+\rho {{b}_{i}}{{v}_{i}}-\rho {{w}_{j}}\frac{\partial e}{\partial {{x}_{j}}}$ | (3) |
式中:ρ为流体密度;v和w为物质速度和对流速度;σij为应力张量;b和e分别为体力和能量。
利用算子分离算法对ALE控制方程(1)~方程(3)进行离散求解,首先执行拉格朗日过程,然后对穿过边界的质量输运、内能和动量等参数进行计算,采用中心差分按照时间递增进行求解。
采用时间显式法,对每个节点,速度和位移按以下等式进行更新:
| ${{u}^{n+1/2}}={{u}^{n-1/2}}+\Delta t{{M}^{-1}}(F_{ext}^{n}+F_{int}^{n}), $ | (4) |
| ${{x}^{n+1}}={{x}^{n-1}}+\Delta t{{u}^{n+1/2}}.$ | (5) |
式中:
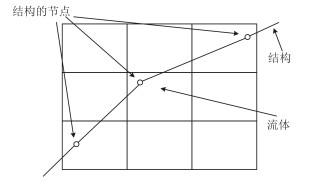
冰层和流体层的耦合采用欧拉-拉格朗日耦合算法,建立几何模型和进行有限元网格划分时,结构与流体的网格重叠,如图 2所示对拉格朗日结构进行约束,将结构的相关参量传递给流体单元。
|
图 2 拉格朗日-欧拉耦合算法 Fig. 2 Lagrange-Euler algorithm |
对冰层的加速度和速度进行约束,流体结构的节点速度按以下公式进行更新。将结构节点的动量分配给流体单元的节点:
| $M_{i}^{f}=M_{i}^{f}+{{h}_{i}}\cdot {{M}_{s}}, $ | (6) |
计算新的流体节点速度:
| $v_{i}^{f}=\frac{M_{i}^{f}}{m_{i}^{f}}, $ | (7) |
约束结构的节点速度:
| ${{v}_{s}}=\underset{i=1, 8}{\mathop{\Sigma }}\, {{h}_{i}}\cdot v_{i}^{f}.$ | (8) |
模拟气垫船的气垫层和冰层采用各向同性线弹性材料,采用对称罚函数方法约束的自动面-面接触算法,气垫压力通过给气垫层加载重力的方式实现。
空气和水采用线性多项式状态方程描述,其内能分布呈线性,压力由下式给出:
| $P={{C}_{0}}+{{C}_{1}}\mu +{{C}_{2}}{{\mu }^{2}}+{{C}_{3}}{{\mu }^{3}}+({{C}_{4}}+{{C}_{5}}\mu +{{C}_{6}}{{\mu }^{2}})E.$ | (9) |
式中:P为压力;C0~C6为状态方程系数;E为弹性模量;
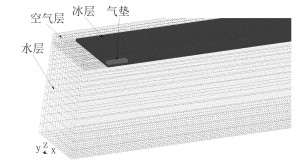
为方便验证计算结果的有效性,本文采用Takizawa试验[6]的实际参数来建立气垫船冰上航行的三维模型。如图 3所示(半个模型),xz为对称面,从下至上依次为水层、冰层、气垫层和空气层,空气层和水层交界处共节点,空气层与冰层、气垫层网格重合。为减小边界影响,冰层在x方向距离前端边界2m,y方向距离外侧边界1m,计算域长L=200 m,宽B=12 m。水层、冰层和空气层的厚度分别为H=6.8 m、h=0.17 m和H1=0.7 m。采用3D实体单元划分网格,单元数为281 040,节点数为325 953。
|
图 3 网格划分 Fig. 3 The meshing of model |
参考Takizawa实验雪地车的尺寸及参数,模型中气垫尺寸取为:长a=2.4 m,宽b=0.8 m,厚c=0.2 m。根据雪地车重量换算得到气垫密度,空气和水的密度分别为1.29 kg/m3和1026 kg/m3,力学特性参数取值如表 1所示。
|
|
表 1 冰层和气垫层的力学特性参数 Tab.1 Parameters of ice sheet and ACV |
为研究不同载荷速度下冰层位移响应,计算时气垫船速度从2~15 m/s取值;此外,为研究岸壁对临界速度的影响,定义河道宽度与雪地车宽度比值为λ=B/b,计算时λ从2~20取值。
3 计算结果与分析 3.1 不同载荷速度下的冰层位移响应取冰层距前端50 m处冰层对称面中层节点为观测点,节点编号为311 880。
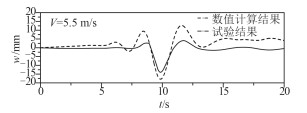
图 4所示为V=5.5 m/s时观测点的位移响应曲线与Takizawa实冰试验结果对比曲线,横坐标为时间t,纵坐标为冰层位移响应w,数值计算过程的前3 s时间进行重力和速度加载,冰层未达到稳定状态,受到浮力作用产生正向位移。载荷从起始点开始运动,产生的小幅波向前传播,冰层发生小幅震荡,载荷运动到观测点附近时,观测点在某一时刻达到最大下陷位移,并且下陷宽度减小,载荷通过后冰层的位移响应减弱,下陷深度减小,下陷宽度变大,位移响应的变化规律一致。
|
图 4 V=5.5 m/s时的冰层位移响应 Fig. 4 Displacement response of V=5.5 m/s |
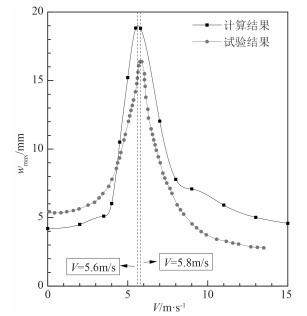
图 5所示为冰层最大下陷位移与载荷速度关系的曲线V,横坐标为载荷速度,纵坐标为最大下陷位移wmax。计算结果表明:在低速区域得到的位移比试验结果小,在临界速度附近以及高速区域,最大下陷位移比试验结果大,由于数值计算存在岸壁边界和前后边界,边界对应力波的反射作用会对冰层的变形产生影响,在临界速度附近,岸壁的反射波对冰层的振动有促进作用;载荷速度较低时,岸壁的反射波对冰层的振动有抑制作用;载荷速度较高时,边界的反射波到达中间区域之前,载荷已向前运动较远距离,反射波来不及对较早产生的位移响应产生影响,对冰层的振动影响较小。此外,从图中还可以看出,计算结果与实验结果的变化规律基本一致。随着载荷速度的增加,冰层下陷位移不断增加,且在特定航速附近冰层下陷位移达到最大值,当载荷速度超过此速度以后,冰层下陷位移反而变小。该现象说明存在使得冰层下陷位移最大的临界速度,气垫船在该速度下航行可以使冰层的振动幅度最大,有利于冰层断裂以达到破冰的目的,而其他移动载荷在冰上航行时应避开该速度。
|
图 5 不同载荷速度下的冰层最大下陷深度 Fig. 5 The maximum depression depth of ice sheet caused by different vehicle speed |
根据文献[14]提供的计算浅水条件下冰上载荷临界速度的2个近似公式(10)和公式(11),代入本文计算参数可以得临界速度的理论解结果分别为Vs=5.8 m/s和Vc=5.9 m/s,该结果与数值计算结果V=5.6 m/s及实验结果相一致。
| ${{V}_{s}}=\sqrt{\frac{2gH}{1-{{{\bar{H}}}^{4}}/90+\sqrt{{{(1+{{{\bar{H}}}^{4}}/90)}^{2}}+{{(1/3+\eta /\bar{H})}^{2}}{{{\bar{H}}}^{4}}}}}, $ | (10) |
| $\begin{align} & {{V}_{c}}=\frac{5D{{k}^{4}}+{{\rho }_{2}}g}{2\sqrt{(5D{{k}^{4}}+{{\rho }_{2}}g)[{{\rho }_{1}}kh+{{\rho }_{2}}\coth (kH)]}}- \\ & \frac{[{{\rho }_{1}}h-{{\rho }_{2}}H{{\sinh }^{2}}(kH)]\sqrt{5D{{k}^{4}}+{{\rho }_{2}}g}}{2{{[{{\rho }_{1}}kh+{{\rho }_{2}}\coth (kH)]}^{3/2}}} \\ \end{align}$ | (11) |
式中Vs和Vc分别为利用奇点法和能量法所得的临界速度。
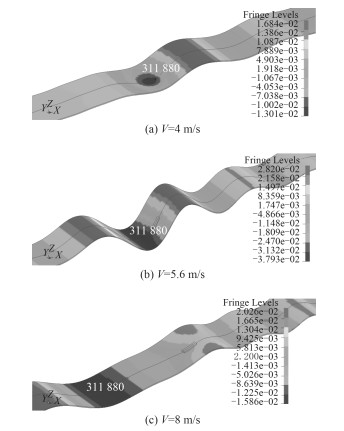
为了更直观地反映气垫船破冰的机理,现考察不同载荷速度下冰层竖直位移变形以及应力云图(见图 6)。当载荷速度为亚临界速度时(见图 6(a)),载荷速度小于冰层能量的传播速度,此时与静态载荷作用的情况类似,冰层最大下陷位移位于载荷正下方,冰-水系统能量不能持续积累;当载荷速度接近临界速度时(见图 6(b)),载荷速度等于冰层能量的传播速度,冰-水系统能量得到持续积累,随着时间推移气垫船将激励冰层产生大幅变形以致冰层破裂;当载荷速度为超临界速度时(见图 6(c)),载荷会越过冰层振动波的波峰,对冰层的变形起到了抑制作用,冰-水系统的能量不能得到持续积累,因此气垫船所激励的冰层位移也极为有限。
|
图 6 不同载荷速度下的冰层竖直位移云图 Fig. 6 The contour map of vertical displacement of ice sheet caused by different ACV speed |
综上所述,虽然数值计算采用的材料模型以及各种耦合算法并不能完全模拟实际情况,但数值计算结果与试验结果所得的曲线整体变化规律一致,这说明,该数值计算方法对于研究气垫船破冰具有一定的指导意义。
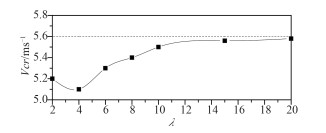
3.2 岸壁宽度对临界速度的影响只改变λ的值,其他参数不变重新进行计算,λ的取值分别为2,4,6,8,10,15,20,通过多次计算估算出不同河道宽度下载荷的临界速度,结果如图 7所示,横坐标为参数λ,纵坐标为临界速度Vcr。
|
图 7 不同λ时的临界速度 Fig. 7 Critical speed with different λ |
从图 7可发现,随着λ减小,岸壁宽度变小,临界速度有变小的趋势;临界速度随着λ增大逐渐趋近5.6 m/s;当λ≥15时,临界速度几乎不变且接近无限大冰层情况下的临界速度,这说明当λ≥15时,岸壁影响可以忽略不计;当λ=4时,临界速度最小,随着岸壁宽度进一步变小,临界速度反而变大,说明存在特定的λ即岸壁宽度使得临界速度最小。
从波和能量的角度分析,岸壁宽度较小时,冰层变形产生的波形会在岸壁反射回来,反射回来的波与冰层变形叠加,使冰层的位移相应增强或减弱,相应的临界速度会发生变化;岸壁宽度过大时,载荷最初激励的波形从岸壁反射回来经过的时间较长,此时载荷已经运动到较远位置,振幅较大的波也向前传播了不少距离,加上反射回来的波能量损失较大,对冰-水系统兴波的能量积累贡献不大。岸壁宽度尺度进一步变大,接近于无限大冰层,反射回来的波对冰层造成的位移影响进一步减小。因此,针对不同河道情况,应选择合适宽度的气垫船和与之对应的临界速度来提高破冰效率。
4 结语在均匀浅水和存在河道岸壁条件下,建立了气垫船航行激励冰层位移响应的三维数值计算方法,并采用动力学分析软件LS-DYNA进行了数值模拟计算,获取了气垫船在不同速度下航行时冰层的位移响应,得到了使得冰层响应最大的临界速度,并与相关试验结果和理论解结果进行对比,验证了计算方法的有效性。基于数值计算结果,分析了河道岸壁宽度对临界速度的影响,结果表明岸壁的存在使得临界速度有所减小,同时还得到了存在使临界速度最小的岸壁宽度这一结论。本文仅针对直岸壁条件下气垫船激励冰层响应作了初步探讨,在实际应用中还有许多需要考虑的因素,如变速航行、非均匀水深、弯曲岸壁等,这是下一步需要研究解决的问题。
| [1] |
于亦凡, 刘军, 周祥龙. 全垫升气垫船控制研究综述[J]. 舰船科学技术 , 2012, 34 (9) :11–15.
YU Yi-fan, LIU Jun, ZHOU Xiang-long. The mat liters hovercraft in control[J]. Ship Science and Technology , 2012, 34 (9) :11–15. |
| [2] |
丁留谦, 何秉顺, 闫新光. 破冰防凌新技术探讨[J]. 中国防汛抗旱 , 2010, 20 (2) :19–24.
DING Liu-qian, HE Bing-shun, YAN Xin-guang. New technology of icebreaking and ice runs[J]. China Flood & Drought Management , 2010, 20 (2) :19–24. |
| [3] |
潘进军, 白美兰. 内蒙古黄河凌汛灾害及其防御[J]. 应用气象学报 , 2008, 19 (1) :106–110.
PAN Jin-jun, BAI Mei-lan. Ice runs of the yellow river and its defense in Inner Mongolia[J]. Journal of Applied Meteorological Science , 2008, 19 (1) :106–110. |
| [4] | MILINAZZO F, SHINBROT M, EVANS N W. A mathematical analysis of the steady response of floating ice to the uniform motion of a rectangular load[J]. Journal of Fluid Mechanics , 1995, 287 :173–197. DOI:10.1017/S0022112095000917 |
| [5] | MELLOR M. Icebreaking concepts[R]. CRREL Special Report, Hanover, New Hampshire:Engineering Lab, 1980. |
| [6] | TAKIZAWA T. Deflection of a floating sea ice sheet induced by a moving load[J]. Cold Regions Science and Technology , 1985, 11 (2) :171–180. DOI:10.1016/0165-232X(85)90015-1 |
| [7] | SQUIRE V A, ROBINSON W H, HASKELL T G, et al. Dynamic strain response of lake and sea ice to moving loads[J]. Cold Regions Science and Technology , 1985, 11 (2) :123–139. DOI:10.1016/0165-232X(85)90012-6 |
| [8] | SQUIRE V A, HOSKING R J, KERR A D. Moving loads on ice plates[M]. The Netherlands: Kluwer Academic Publishers, 1996 . |
| [9] |
胡明勇, 张志宏, 刘巨斌, 等. 脉冲载荷作用下冰层的动力学研究[J]. 海军工程大学学报 , 2011, 23 (6) :5–7.
HU Ming-yong, ZHANG Zhi-hong, LIU Ju-bin, et al. Dynamic response of viscoelastic floating ice plate (VFIP) under unit-impulse loading[J]. Journal of Naval University of Engineering , 2011, 23 (6) :5–7. |
| [10] |
胡明勇, 张志宏, 刘巨斌. 三角脉冲载荷作用下黏弹性浮冰的瞬态响应[J]. 华中科技大学学报(自然科学版) , 2014, 42 (1) :53–57.
HU Ming-yong, ZHANG Zhi-hong, LIU Ju-bin. Transient response of viscoelastic floating ice plate under triangular pulse load[J]. Journal of huazhong university of Science and Technology (Natural Science Edition) , 2014, 42 (1) :53–57. |
| [11] |
胡明勇, 张志宏, 顾建农, 等. 正弦荷载作用下浮冰的稳态响应近似解析解[J]. 华中科技大学学报(自然科学版) , 2012, 40 (2) :58–61.
HU Ming-yong, ZHANG Zhi-hong, GU Jian-nong, et al. Approximate analytical solutions of steady response of floating ice plate under sinusoidal loading[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition) , 2012, 40 (2) :58–61. |
| [12] |
刘巨斌, 张志宏, 张辽远, 等. 边界元-有限差分混合方法在气垫船破冰数值模拟中的应用[J]. 海军工程大学学报 , 2013, 25 (3) :50–55.
LIU Ju-bin, ZHANG Zhi-hong, ZHANG Liao-yuan, et al. Application of mixed BEM and FDM in numerical simulation of ice-breaking by air cushion vehicle[J]. Journal of Naval University of Engineering , 2013, 25 (3) :50–55. |
| [13] |
刘巨斌, 张志宏, 张辽远, 等. 气垫船兴波破冰问题的数值计算[J]. 华中科技大学学报(自然科学版) , 2012, 40 (4) :91–95.
LIU Ju-bin, ZHANG Zhi-hong, ZHANG Liao-yuan, et al. Numerical computation of broken ice by air-cusion vehicles in wave making[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition) , 2012, 40 (4) :91–95. |
| [14] |
张志宏, 顾建农, 王冲, 等. 航行气垫船激励浮冰响应的模型实验研究[J]. 力学学报 , 2014, 46 (5) :655–664.
ZHANG Zhi-hong, GU Jian-nong, WANG Chong, et al. Model experiment about of response on floating ice sheet subjected to moving air cushion vehicle[J]. Chinese Journal of Theoretical and Applied Mechanics , 2014, 46 (5) :655–664. |
| [15] |
卢再华, 张志宏, 胡明勇, 等. 全垫升式气垫船破冰过程的数值模拟[J]. 振动与冲击 , 2012, 31 (24) :148–154.
LU Ju-bin, ZHANG Zhi-hong, HU Ming-yong, et al. Numerical simulation for ice-breaking process of an amphibian air cushion vehicle[J]. Journal of Vibration and Shock , 2012, 31 (24) :148–154. |
| [16] |
卢再华, 张志宏, 胡明勇, 等. 气垫船破冰机理分析及临界航速估计[J]. 船舶力学 , 2014, 18 (8) :916–923.
LU Zai-hua, ZHANG Zhi-hong, HU Ming-yong, et al. Analysis on the ice-breaking mechanism of air cushion vehicle and the critical speed estimation[J]. Journal of Ship Mechanics , 2014, 18 (8) :916–923. |
 2016, Vol. 38
2016, Vol. 38
