2. 西安交通大学 化工学院, 陕西 西安 710049
2. School of Chemical Engineering and Technology, Xi'an Jiaotong University, Xi'an 710049, China
制冷系统对温室效应的影响包括两方面:制冷剂泄漏和系统能耗所产生的 CO2 排放。为了降低制冷剂对温室效应的作用, Lorrentzen 提出使用自然工质 CO2 作为替代制冷剂, 并考虑 CO2 高临界压力、低临界温度的特点, 设计了跨临界 CO2 制冷循环。自 20 世纪 90 年代以来, 国内科研院所对 CO2 在船用制冷系统中应用的研究方兴未艾, 由于传统的跨临界 CO2 制冷循环中, 存在高低压差大, 节流过程能量损失严重, 系统性能较差。为了降低节流损失, 有学者提出跨临界 CO2 引射制冷循环, 使用引射器代替节流阀回收部分高压能, 从而提高系统性能。目前已有很多学者就跨临界 CO2 引射制冷循环进行理论和实验研究[1, 2], 研究显示引射器的使用对系统性能有很大提高。此外, 动态性能是制冷系统研究的另一个重要方面, 是系统控制系统设计的基础, 然而目前鲜有跨临界 CO2 引射制冷系统动态性能的研究成果发表。
本文针对跨临界 CO2 两相流引射制冷系统, 通过 Matlab 软件建立动态模型, 研究在各设备运行参数阶跃扰动下系统的动态性能, 为系统控制策略设计提供依据。
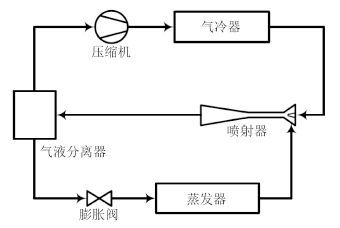
1 系统流程及动态模型 1.1 跨临界 CO2 引射制冷循环流程典型跨临界 CO2 引射制冷循环流程如图 1 所示, 引射器的结构如图 2 所示。高压超临界 CO2 在气冷器中放热降温, 作为主动流在引射器喷嘴中产生膨胀, 在喷嘴出口产生低压超音速两相流, 在引射段引射来自蒸发器的过热 CO2, 两流体在混合段产生混合动量交换, 压力升高, 通过扩压段再次提升压力, 在引射器出口获得中间压力的两相 CO2; 流体经过气液分离器分离, 气相 CO2 通过压缩机升压升温进入气冷器, 完成高压循环; 液相 CO2 在膨胀阀中节流产生低压流体进入蒸发器完成低压循环。因此, 引射器通过利用高压侧流体的压力引射低压流体, 获得中间压力, 降低了节流损失和压缩功, 从而提高系统的性能。
|
图 1 跨临界 CO2 引射制冷系统流程 Fig. 1 Transcritical CO2 two-phase ejector expansion refrigeration system drawing |
|
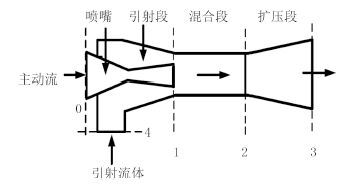
图 2 引射器结构图 Fig. 2 Ejector structure drawing |
本文在建立各设备动态模型的基础上, 通过分析设备之间的质量、能量守恒关系, 模拟计算系统的动态性能, 分析在压缩机转速、膨胀阀开度及喷射器喷嘴尺寸阶跃扰动下, 系统各参数的阶跃响应。
1.2 系统动态模型在建立系统各设备模型时, 考虑蒸发器、气冷器、气液分离器为工质存储设备, 惯性作用较大, 时间常数大, 有延迟效应, 选择动态模型; 而压缩机、膨胀阀、引射器作为流量控制设备, 时间常数小, 为了降低计算的复杂度, 选用稳态模型, 并不会对系统动态性能有很大影响。
蒸发器采用套管式换热器, 二级流体为水, 并假设出口总处于过热状态。在蒸发器中, 换热过程可分为两相相变换热区和单相过热换热区 2 个区。为了在模型中反映不同的换热段, 蒸发器模型选择移动边界模型。该模型在制冷系统动态分析中经常使用, 降低了模型计算复杂度, 同时能够反应蒸发器中由相变换热到单相换热的特点。
气冷器中 CO2 为超临界态, 换热过程不存在相变, 采用套管式换热器, 二级流体为水。模型采用集总参数模型。该方法通过建立气冷器质量守恒、能量守恒的偏微分方程, 沿管长方向积分, 从而获得设备常微分方程组。具体的换热器模型建立过程可参考文献[3], 二氧化碳的换热系数计算采用文献[4, 5]的经验公式计算。
压缩机稳态模型基于流量和能量方程, 设备容积效率和等熵效率使用文献[6, 7]所提供的经验公式; 膨胀阀中的膨胀过程假设为等焓节流过程, 流量由孔板节流流量计算公式计算, 具体公式参考文献[8]。
如图 2 所示, 引射器包括喷嘴、引射段、混合段、扩压段 4 个部分。假设流体在入口、出口处速度为 0; 喷嘴出口压力等于蒸发压力, 引射流体在引射段内没有膨胀过程; 混合段中主动流与引射流压力相同, 是恒压混合过程。对每个部分建立质量、能量及动量守恒方程, 所得模型如式(1) ~式(7) 所示:
| ${\eta _n} = ({h_0}-{h_1})/({h_0}-{h_{1s}})\text{, }$ | (1) |
| $0.5u_1^2 = {h_0}-{h_1}\text{, }$ | (2) |
| ${u_2} = {u_1}/(\mu + 1) \text{, }$ | (3) |
| ${\eta _m} = {u_{2'}}/{u_2}\text{, }$ | (4) |
| ${h_3}-{h_2} = 0.5u_{2'}^2\text{, }$ | (5) |
| ${h_3} = ({h_0} + {h_4}\mu )/(\mu + 1) \text{, }$ | (6) |
| ${\eta _d} = ({h_{3s}}-{h_2})/({h_3}-{h_2})\text{。}$ | (7) |
式中的等熵系数采用文献[2]所提供的值, 假设 ηn 为 0.7, ηm 为 0.95, ηd 为 0.8。
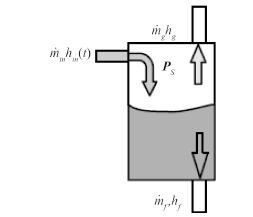
气液分离器模型如图 3 所示。应用质量、能量守恒方程, 选择压力和制冷剂储量为状态变量, 建立状态空间形式的动态模型如式(8) ~式(10) 。
| $\left[\!\! {\begin{array}{*{20}{c}} 1& 0\\ {Am}& {Ap} \end{array}} \!\!\right]\left[{\begin{array}{*{20}{c}} {\mathop {{m_s}}\limits^ \bullet }\\ {\mathop {{p_s}}\limits^ \bullet } \end{array}} \right] \!=\! \left[{\begin{array}{*{20}{c}} {\mathop {{m_{s, in}}}\limits^ \bullet -\left( {\mathop {{m_g}}\limits^ \bullet + \mathop {{m_f}}\limits^ \bullet } \right)}\\ {{m_{s, in}}{h_{s, in}}-{m_g}{h_g}-{m_f}{h_f}} \end{array}} \right]\text{, }$ | (8) |
式中系数:
| $Am = \frac{{{\rho _g}{u_g}-{\rho _f}{u_f}}}{{{\rho _g}-{\rho _f}}}\text{, }$ | (9) |
| $\begin{aligned} Ap = & \frac{{{\rm d}{\rho _g}}}{{{\rm d}{p_s}}}{V_g}{u_g} + \frac{{{\rm d}{\rho _f}}}{{{\rm d}{p_s}}}{V_f}{u_f} + \frac{{{\rm d}{u_g}}}{{{\rm d}{p_s}}}{V_g}{\rho _g} + \frac{{{\rm d}{u_f}}}{{{\rm d}{p_s}}}{V_f}{\rho _f}-\\ & \frac{{{\rho _g}{u_g}-{\rho _f}{u_f}}}{{{\rho _{\rm{g}}}-{\rho _f}}}\left( {\frac{{{\rm d}{\rho _g}}}{{{\rm d}{p_s}}}{V_g} + \frac{{{\rm d}{\rho _f}}}{{{\rm d}{p_s}}}{V_f}} \right)\text{。} \end{aligned}$ | (10) |
|
图 3 气液分离器模型 Fig. 3 Gas-Liquid separator model drawing |
根据图 1 中所示的系统流程, 本文设计的设备主要参数如表 1 所示。
|
|
表 1 系统设备主要参数表 Tab.1 The system parts’main parameters |
在模拟计算时, 考虑初始稳态工况如表 2 所示。将本文开发的模型应用于上述系统稳态工况, 在 Matlab 中模拟计算系统的动态性能。稳态工况下, 2 s 时引射器喷嘴面积阶跃降低 5%; 在一定时间的稳定后, 在 100 s 时膨胀阀开度阶跃降低 5%; 该阶段稳定后, 在 200 s 时压缩机转速突然阶跃增加 5%。根据上述一系列扰动下计算主要系统参数动态响应。
|
|
表 2 仿真计算初始稳态工况 Tab.2 The original steady condition by simulation |
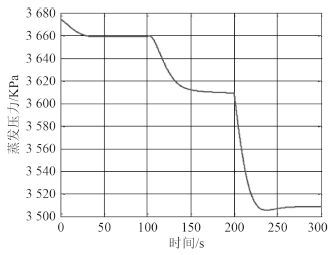
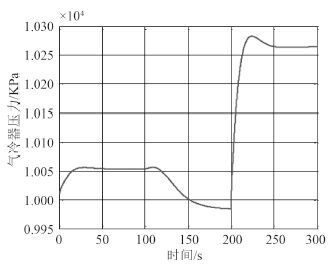
如图 4~图 7 和表 3 计算结果所示, 在初始喷嘴面积减少时, 喷嘴中膨胀作用增强, 喷嘴出口压力降低, 引射作用增强, 使得蒸发器液体储量减少, 压力降低; 同时主动流流量减少, 气冷器出口流量突然减低, 导致压力升高; 引射器混合流体变化小, 气液分离器的储液量变化较小。所以在喷嘴出口面积减少时, 更多的 CO2 将向气冷器中集中。
|
图 4 蒸发压力动态响应 Fig. 4 The dynamic response of evaporator pressure |
|
图 5 气冷器压力的动态响应 Fig. 5 The dynamic response of gas cooler pressure |
|
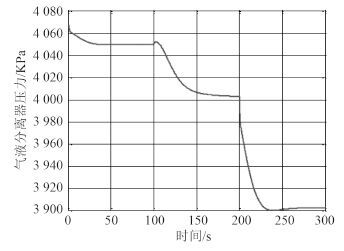
图 6 气液分离器压力的动态响应 Fig. 6 The dynamic response of gas-liquid separator pressure |
|
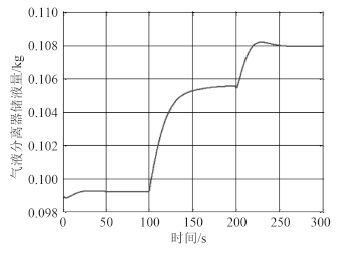
图 7 储液量的动态响应 Fig. 7 The dynamic response of supplying quantity |
|
|
表 3 相同时间下系统参数动态变化 Tab.3 The system parameters’dynamic trends under same time rate of change |
当膨胀阀开度减少时, 进入蒸发器的流量减少, 蒸发压力降低, 导致引射流量减少; 在较大的喷嘴膨胀压差作用下, 主动流流量增加, 气冷器压力降低。在膨胀阀开度降低时, CO2 将向气液分离器集中, 气液分离器中液位上升。
当压缩机转速增加时, 更多的气相 CO2 压缩进入气冷器中, 气冷器压力升高, 主动流引射作用增强, 引射蒸发器中的过热 CO2, 使得蒸发器压力降低; 气液分离器中气相减少, 压力降低, 液位升高。另外, 从图中分析可知, 在相同时间(100s)变化的扰动下, 系统参数对压缩机转速扰动更敏感。
结合本文将开展的系统运行参数控制方面的研究, 从图 4~图 7 也可以看出, 不同的控制输入对系统各参数都有很明显的作用, 系统输入输出通道之间有强烈耦合作用, 多通道 SISO 控制器的设计存在困难, 而且效果可能较差; 图中显示在膨胀阀开度阶跃变化时会产生逆向响应, 即系统模型存在 RHP 零点, 这一性质将限制系统响应速度, 膨胀阀开度扰动下系统稳定时间长也验证了这一结论, 同时 RHP 零点也会增加控制器设计的复杂度。
3 结语本文通过建立的船用跨临界 CO2 两相流引射制冷系统的动态模型, 在一定尺寸的设备及稳态工况下, 通过 Matlab 求解模型, 获得了系统运行参数(蒸发压力、气冷器压力、气液分离器压力和储液量)在压缩机转速、膨胀阀开度、引射器喷嘴尺寸的阶跃扰动下的动态响应。分析结果显示:
1) 系统运行参数, 尤其是各运行压力对压缩机转速更加敏感;
2) 在膨胀阀作为扰动输入的通道中存在 RHP 零点, 表现在 100 s 膨胀阀开度出现扰动时, 系统运行参数, 如蒸发压力、气冷器压力和气液分离器压力均先短时上升后再快速下降, 会产生逆向响应;
3) 系统各输入对所有系统参数都有明显作用, 耦合作用强烈。这些动态特性会增加制冷系统控制器设计的复杂度, 而本文关于动态特性的研究对系统控制器的设计有重要的指导意义。
| [1] | LEE J S, KIM M S, KIM M S. Experimental study on the improvement of CO2 air conditioning system performance using an ejector[J]. International Journal of Refrigeration , 2011, 34 (7) :1614–1625. DOI:10.1016/j.ijrefrig.2010.07.025 |
| [2] | DENG J Q, JIANG P X, LU T, et al. Particular characteristics of transcritical CO2 refrigeration cycle with an ejector[J]. Applied Thermal Engineering , 2007, 27 (2/3) :381–388. |
| [3] | ALLEYNE A G, RASMUSSEN B P. Control-oriented modeling of transcritical vapor compression systems[J]. Journal of Dynamic Systems, Measurement and Control , 2004, 126 (1) :54–64. DOI:10.1115/1.1648312 |
| [4] | YOON S K, KIM J H, HWANG Y W, et al. Heat transfer and pressure drop characteristics during the in-tube cooling process of carbon dioxide in the supercritical region[J]. International Journal of Refrigeration , 2003, 26 (8) :857–864. DOI:10.1016/S0140-7007(03)00096-3 |
| [5] | KIM M H, BULLARD C W. Development of a microchannel evaporator model for a CO2 air-conditioning system[J]. Energy , 2001, 26 (10) :931–948. DOI:10.1016/S0360-5442(01)00042-1 |
| [6] |
刘洪胜, 杨涛, 陈江平, 等. 跨临界二氧化碳制冷系统动态性能仿真研究[J]. 工程热物理学报 , 2006, 27 (S2) :69–72.
LIU Hong-sheng, YANG Tao, CHEN Jiang-ping, et al. Research on dynamic simulation of transcritical CO2 refrigeration system[J]. Journal of Engineering Thermophysics , 2006, 27 (S2) :69–72. |
| [7] |
杨涛, 陈江平, 陈芝久. 二氧化碳汽车空调系统的动态仿真[J]. 上海汽车 , 2007 (6) :15–19.
YANG Tao, CHEN Jiang-ping, CHEN Zhi-jiu. The dynamic simulation of the air condition system of the CO2 in vehicle[J]. Shanghai Auto , 2007 (6) :15–19. |
| [8] |
张早校, 冯霄, 郁永章.
制冷与热泵[M]. 北京: 化学工业出版社, 2000 .
ZHANG Zao-xiao, FENG Xiao, YU Yong-zhang. Refrigeration and Heat Pump[M]. Beijing: Chemical Industry Press, 2000 . |
 2016, Vol. 38
2016, Vol. 38
