2. 中国人民解放军92840部队, 山东 青岛 266405
2. No. 92840 Unit of PLA, Qingdao 266405, China
在海上动态情况下的舰艇作战系统对准过程中, 被检设备的测量数据必须利用船姿数据经过坐标平移和旋转后才能转化为地理坐标系数据, 从而消除或修正舰艇姿态对测量结果的影响。目前, 舰艇上安装的导航设备一般为惯性导航设备(简称“惯导”), 由于惯导本身固有的缺点, 惯导所提供的舰艇姿态信息含有系统误差, 各被检设备依据惯导提供的舰艇姿态信息进行坐标转换时会引入新的误差。因此, 需要寻找其他高精度的舰艇姿态测量手段。
与目前广泛应用的惯导系统相比, 由于具有价格低、初始化时间短、精度高、无累积误差等优点, 基于导航卫星的多天线舰艇姿态测量系统已成为目前研究的热点[1]。北斗卫星导航系统(以下简称北斗)是我国自主建设、独立运行, 并与世界其他卫星导航系统兼容共用的全球卫星导航系统, 研究基于北斗系统的高精度舰艇定姿技术具有重要意义。
1 基于导航卫星的舰艇姿态测量原理所谓舰艇的姿态, 是指舰艇甲板坐标系相对于舰艇地理坐标系(当地水平坐标系)的方位关系, 由航向角 CW、纵摇角 Ψ 和横摇角 θ 三个姿态角来表示[2]。基于导航卫星的舰艇姿态测量是指将 2 ~ 4 个卫星信号接收天线采用天线配置技术安装在舰艇甲板上, 在天线间固定基线长度的情况下, 利用各天线接收卫星信号的载波相位观测值, 求在当地水平坐标系下天线间的基线向量解, 根据姿态转换矩阵与各天线的相对位置的函数关系求解舰艇的姿态角参数。使用 3 根不共线的天线垂直配置, 形成双基线测量系统, 就可以完成舰艇三维姿态的测量[3]。在一般情况下, 天线 1 作为主天线位于舰艇甲板坐标系的原点, 天线 2 和天线 3 分别位于舰艇甲板坐标系的 Y 轴和 X 轴。实际上, 测量舰艇的姿态需要求解天线 1 和天线 2 间的航向角和纵摇角, 及求解天线 1 和 3 之间的俯仰角作为横摇角[4]。
舰艇姿态测量是求解短基线下接收机天线相对位置的问题, 根据舰艇甲板的实际情况可知, 基线长度一般在几米到几十米。对于这种短基线来说, 双差后电离层延迟和对流层延迟基本上被消除。因此, 在舰艇姿态测量中, 以基线
| $\begin{array}{l} \lambda \nabla \Delta \varphi _{12}^{mn} = (\vec e_1^n-\vec e_1^m) \cdot {{\vec b}_{12}}-\lambda \nabla \Delta N_{12}^{mn} + \nabla \Delta \varepsilon _{12}^{mn} =\\ \, \, \left[{\begin{array}{*{20}{c}} {\nabla l_1^{mn}} \!\! & \!\! {\nabla m_1^{mn}} \!\! & \!\! {\nabla n_1^{mn}} \end{array}} \right] \!\! \cdot \!\! \left[{\begin{array}{*{20}{c}} {{b_x}}\\ {{b_y}}\\ {{b_z}} \end{array}} \right] \!\! - \!\! \lambda \nabla \Delta N_{12}^{mn} \!\! + \!\! \nabla \Delta \varepsilon _{12}^{mn}\text{。} \end{array}$ | (1) |
式中:λ 为载波波长;
| $\nabla l_u^{mn} = \frac{{{x_m}-{x_u}}}{{{R_{um}}}}-\frac{{{x_n}-{x_u}}}{{{R_{un}}}}\text{, }$ | (2) |
| $\nabla m_u^{mn} = \frac{{{y_m}-{y_u}}}{{{R_{um}}}}-\frac{{{y_n}-{y_u}}}{{{R_{un}}}}\text{, }$ | (3) |
| $\nabla n_u^{mn} = \frac{{{z_m}-{z_u}}}{{{R_{um}}}}-\frac{{{z_n}-{z_u}}}{{{R_{un}}}}\text{。}$ | (4) |
式中:
| ${R_{um}} = \sqrt {{{({x_u}-{x_m})}^2} + {{({y_u}-{y_m})}^2} + {{({z_u}-{z_m})}^2}} \text{, }$ | (5) |
| ${R_{un}} = \sqrt {{{({x_u}-{x_n})}^2} + {{({y_u}-{y_n})}^2} + {{({z_u}-{z_n})}^2}} \text{。}$ | (6) |
假设 t 时刻天线 1 和天线 2 能同时观测到的卫星数目为 n(n ≥ 5) , 则可以构成(n-1) 个双差观测方程, 这里假设观测到的卫星分别为 m, n, p, q, s, 且设卫星 m 为主星, 忽略观测噪声, 则将双差方程写成矩阵形式有:
| $\lambda \cdot \left[{\begin{array}{*{20}{c}} {\nabla \Delta \varphi _{12}^{mn}}\\ {\nabla \Delta \varphi _{12}^{mp}}\\ {\nabla \Delta \varphi _{12}^{mq}}\\ {\nabla \Delta \varphi _{12}^{ms}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\vec e_1^m-\vec e_1^n}\\ {\vec e_1^m-\vec e_1^p}\\ {\vec e_1^m-\vec e_1^q}\\ {\vec e_1^m-\vec e_1^s} \end{array}} \right] \cdot {\vec b_{12}}-\lambda \left[{\begin{array}{*{20}{c}} {N_{12}^{mn}}\\ {N_{12}^{mp}}\\ {N_{12}^{mq}}\\ {N_{12}^{ms}} \end{array}} \right]\text{。}$ | (7) |
因此, 一旦确定了整周模糊度的大小, 就能够解算出基线向量
整周模糊度的正确求解, 是利用载波相位测量进行卫星高精度舰艇姿态测量的关键问题。正确解算出整周模糊度, 载波相位观测值即可转化为高精度的站星距离测量值, 进而实现高精度的姿态测量。因此, 整周模糊度的快速解算问题是进行卫星高精度定姿定位的关键问题, 并产生了很多方法, 主要可分为基于测量域、观测域、位置域和模糊度域的整周模糊度求解方法[6]。但这些方法主要针对 GPS 提出, 上述方法不一定适用于北斗系统。
其中, 基于位置域的整周模糊度解算方法, 主要是指模糊度函数法(Ambiguity Function Method, AFM)。模糊度函数法只利用载波相位观测值的小数部分, 因此它对周跳不敏感, 并且可见星数目越多, 模糊度解算的可靠性和成功率越高[7]。但其缺点是搜索空间大而导致搜索时间长和计算量大, 难以实现实时动态定位。北斗系统的星座构型是区别于其他 GNSS 的特点之一, 通过对北斗的星座构型分析, 可以发现北斗系统 GEO 卫星的 z 轴双差方向余弦系数远远小于 x 轴和 y 轴, 因此, 可以将传统的模糊度函数法的三维搜索改进为二维搜索, 提高了搜索效率, 减小了计算量, 从而实现整周模糊度的快速固定。
2.1 模糊度函数法解算原理模糊度函数定义为[8]:
| $\begin{aligned} & A\left( {X, Y, Z} \right) = \sum\limits_{k = 1}^K {\left| {\sum\limits_{j = 1}^{J-1} {\sum\limits_{l = 1}^L {\exp \times } } } \right.} \\ \quad \quad & \left. {\left\{ {i2\pi \left[{\nabla \Delta \varphi _{obs}^{jkl}\left( {{X_0}, {Y_0}, {Z_0}} \right) \!- \!\nabla \Delta \varphi _{cal}^{jkl}\left( {X, Y, Z} \right)} \right]} \right\}} \right| \end{aligned}$ | (8) |
式中:K 为历元数; J 为每历元同步观测到的卫星数; L 为观测所用的频率个数;
| $\begin{aligned} \nabla \Delta \varphi _{cal}^{jkl}\left( {X, Y, Z} \right) = & {\lambda ^{-1}}\left[{\rho _u^i-\rho _r^i-(\rho _u^j-\rho _r^j)} \right] = \\ & {\lambda ^{-1}}\left[{(\vec e_r^i-\vec e_r^j) \cdot {{\vec b}_{ur}}} \right] = \\ & {\lambda ^{-1}}(\nabla l_u^{mn}{b_x} + \nabla m_u^{mn}{b_y} + \nabla n_u^{mn}{b_z})\text{。} \end{aligned}$ | (9) |
由模糊度函数定义可知, 当
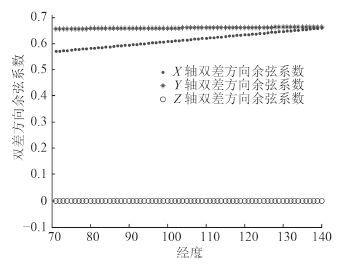
目前, 北斗系统星座构型为 5GEO + 5IGSO + 4MEO 混合星座。通常情况下, 在我国及周边地区一般可以观测到 8~12 颗卫星, 其中包含 3~5 GEO 卫星[9]。GEO 卫星为地球静止轨道卫星, 位于赤道上空同一轨道面上。根据式(2) ~式(4) 计算 GEO 卫星的三维差分方向余弦系数, 如图 1 所示在北纬 50° 地区对 G3 和 G4 星的三维差分方向余弦系数随经度变化的结果。由图 1 可以看出, GEO 卫星的 z 轴的方向余弦系数
|
图 1 GEO 双差方向余弦系数分析结果 Fig. 1 Result of GEO double differential direction cosine coefficient analysis |
基于降维的位置域模糊度解算具体步骤如下:
1) 在利用模糊度函数法进行模糊度解算时, 为了提高搜索的效率, 可以利用原始观测量组成波长较长的宽巷组合。一般的北斗民用接收机可以接收到 B1 和 B2 两个频率上的信号, 这 2 个信号可以形成宽巷组合(B1-B2), 组合频率为 353.985 MHz, 波长 λML 为 0.874 m。
2) 平面搜索。采用(B1-B2)宽巷组合, 由上面的分析可知, Z 轴误差的影响可以忽略, 式(9) 可以写成:
| $\nabla \Delta \varphi _{cal}^{jkl}\left( {X, Y, {Z_0}} \right) = {\lambda ^{-1}}(\nabla l_u^{mn}{b_x} + \nabla m_u^{mn}{b_y} + \nabla n_u^{mn}{b_{z0}})$ | (10) |
式中:
| $\begin{aligned} & A\left( {X, Y, Z} \right) = \frac{1}{{{J_g}-1}}\sum\limits_{j = 1}^{{J_g}-1} {\exp \times } \\ & \quad \left\{ {i2\pi \left[{\nabla \Delta \varphi _{obs}^{jl}\left( {{X_0}, {Y_0}, {Z_0}} \right)-\nabla \Delta \varphi _{cal}^{jl}\left( {X, Y, Z} \right)} \right]} \right\}\text{, } \end{aligned}$ | (11) |
式中 Jg 为可观测的 GEO 卫星数。
改变 X 和 Y 坐标进行搜索, 在峰值点处找到正确的 X 和 Y 坐标。由于只使用 GEO 卫星观测值, 在观测卫星数较少的情况下, 由于载波相位的周期性, 模糊度函数表现为多峰分布的复杂非线性函数。
若设定阈值为 R, 根据
3) z 轴搜索。对应每个坐标点
| $\begin{aligned} & A\left( {{X_l}, {Y_l}, Z} \right) = \frac{1}{{J-1}}\sum\limits_{j = 1}^{J-1} {\exp } \times \\ & \left\{ {i2\pi \left[{\nabla \Delta \varphi _{obs}^{jl}\left( {{X_0}, {Y_0}, {Z_0}} \right)-\nabla \Delta \varphi _{cal}^{jl}\left( {X, Y, Z} \right)} \right]} \right\}\text{。} \end{aligned}$ | (12) |
根据确定的
4) 采用 B1 频点上的测量值在上一步确定的点
根据北斗 GEO 卫星的特点, 在初始定位误差较小的情况下, 可以忽略 z 轴误差带来的影响。对于式(13) 中的
| $\begin{array}{l} \lambda \nabla \Delta \varphi _{rk}^{mn} = (\vec e_u^n-\vec e_u^m) \cdot {{\vec b}_{rk}}-\lambda \nabla \Delta N_{rk}^{mn} + \nabla \Delta \varepsilon _{rk}^{mn} =\\ \left[{\begin{array}{*{20}{c}} {\nabla l_r^{mn}} & {\nabla m_r^{mn}} \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {{b_x}}\\ {{b_y}} \end{array}} \right] + \nabla n_r^{mn} \cdot {b_z} -\\ \lambda \nabla \Delta N_{ur}^{mn} + \nabla \Delta \varepsilon _{rk}^{mn} \end{array}$ | (13) |
式(13) 即为 GEO 卫星的降维双差模型。
具体的基于北斗降维的舰艇定姿算法如下:
1) 利用 B1 和 B2 频点上的观测量形成宽巷组合(B1-B2), 根据初始伪距值计算宽巷模糊度初始值
| $\nabla \Delta N_0^{mn} = \frac{{{f_{B1}}{\rho _{B1}} + {f_{B2}}{\rho _{B2}}}}{{{f_{B1}} + {f_{B2}}}} \cdot \frac{{{f_{B1}}-{f_{B2}}}}{c}-({\varphi _{B1}}-{\varphi _{B2}})\text{。}$ | (14) |
式中:
2) 求解一组基线向量候选值。
选择 3 颗二维几何构型较好的 GEO 卫星组成 2 个双差观测方程, 根据式可得到方程组:
| $\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \lambda \nabla \Delta \varphi _{rk}^{mn} = \left[{\begin{array}{*{20}{c}} {\nabla l_r^{mn}} & {\nabla m_r^{mn}} \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {{b_x}}\\ {{b_y}} \end{array}} \right]+\\ \nabla n_r^{mn} \cdot {b_{z0}}-\lambda \nabla \Delta N_{ur}^{mn}\text{, } \end{array}\\ \begin{array}{l} \lambda \nabla \Delta \varphi _{rk}^{mp} = \left[{\begin{array}{*{20}{c}} {\nabla l_r^{mp}} & {\nabla m_r^{mp}} \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {{b_x}}\\ {{b_y}} \end{array}} \right]+ \\ \nabla n_r^{mp} \cdot {b_{z0}}-\lambda \nabla \Delta N_{ur}^{mp}\text{。} \end{array} \end{array}} \right.$ | (15) |
设初始伪距测量误差范围为 ± l m, 则
根据基线长度约束
对每 1 组
| ${b_{zi}} = \pm \sqrt {{{\left| {\vec b} \right|}^2}-b_{xi}^2-b_{yi}^2} \text{。}$ | (16) |
根据式(16) 可得 l 个基线解, 表示为
3) 根据判决准则求解最优基线向量
在上一步求得的 l 个解中, 只有一个最优解, 最接近于基线向量的真实值。通过适当的判决准则可以找出这个最优解。本文的判决准则采用模糊度函数, 模糊度函数定义为:
| $\begin{aligned} A({b_x}, {b_y}, {b_z}) \!=\! & \frac{1}{{N-1}}\!\!\sum\limits_{i = 1}^{N-1} \!\!{\exp \left\{ {i2\pi } \right.} \left[{\nabla \Delta {\varphi _{obs}}({b_{x0}}, {b_{y0}}, {b_{z0}})-} \right.\\ & \left. {\left. {\nabla \Delta {\varphi _{cal}}({b_x}, {b_y}, {b_z})} \right]} \right\}\text{。} \end{aligned}$ | (17) |
将所有可观测卫星的宽巷双差载波相位观测值和 l 个基线解代入式, 利用
4) B1 频点模糊度求解。以第 3 步计算得到的最优基线向量为初始基线向量, 利用 B1 频点观测值形成 2 个双差观测方程, 按照第 2 步, 得到精确的 B1 频点的模糊度。
5) 利用已知整周模糊度的 B1 频点的高精度载波相位测量值进行舰艇姿态解算。
4 算法仿真本文采用和芯星通的 UR240 双频接收机在短基线下采集的北斗数据进行算法验证。天线 1 位于舰艇甲板坐标系的原点, 天线 2 位于舰艇首尾线上, 距离天线 15 m, 2 根天线组成单基线, 用来测量舰艇的航向角和纵摇角。仿真采用的测站位置为 39.54° N, 115.28° S, 高度为 5.31 m。星历数据为 2015-8-22 09:08:00 ~ 2015-8-23 09:08:00 的北斗实际星历, 设 σφ = 0.005 m, σp = 0.8 m[10], 采样间隔为 30 s。
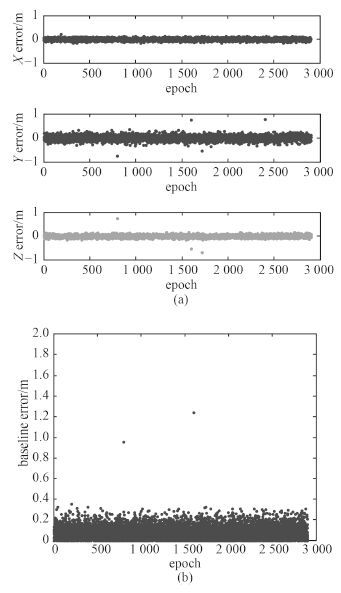
首先, 利用 B1 和 B2 频点的组合观测量进行宽巷结算, 结果如图 3 所示, 其中图 3(a)为 3 轴方向上的向量误差, 其中 z 轴误差在 0.2 m 以内, 表明可以忽略 z 轴误差的影响; 图 3(b)为三维误差, 误差在 0.4 m 以内。
|
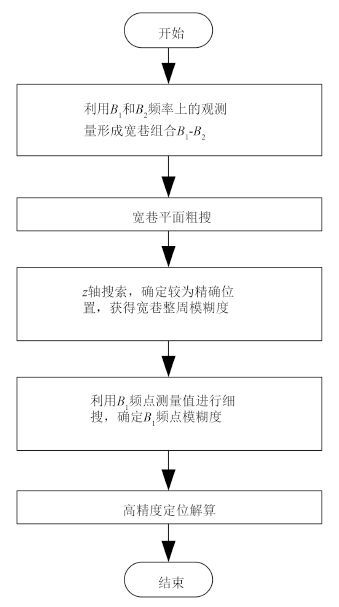
图 2 改进的模糊度函数法解算流程 Fig. 2 Improved ambiguity function method solving process |
|
图 3 宽巷求解后的基线误差 Fig. 3 Baseline error after widelane solving |
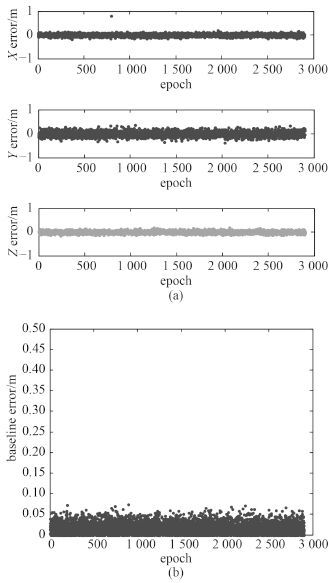
然后, 利用宽巷结算的结果作为初始基线向量解进行 B1 频点模糊度求解。求解所得的解算误差如图 4所示, 图 4(a)和图 4(b)分别为 3 轴方向上的误差和三维误差。
|
图 4 B1 频点求解后的基线误差 Fig. 4 Baseline error after B1 frequency point solving |
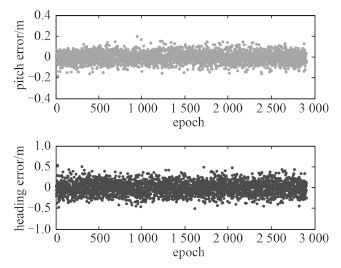
最后, 利用 B1 频点解算结果进行舰艇的航向角和纵摇角解算, 结果如图 5 所示, 航向角的标准差为 0.16°, 纵摇角的标准差为 0.07°。
|
图 5 单基线定向解算误差 Fig. 5 Single baseline orientation solving error |
本文根据北斗 GEO 卫星的特殊星座构型, 提出了一种基于北斗的降维双差模型的舰艇快速定姿算法。该方法利用降维解算方法将模糊度函数法的搜索范围从三维转化为二维, 再利用模糊度函数法作为判决准则确定整周模糊度, 并采用先求宽巷模糊度后求单个频点模糊度的方法, 进一步减少了模糊度解算的计算量。利用北斗实测数据仿真验证, 结果表明该方法解算 B1 频点模糊度成功率高, 确定的航向角标准差为 0.16°, 纵摇角标准差为 0.07°, 是一种快速高效的舰艇定姿算法。
| [1] |
杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学: 地球科学 , 2014, 57 (1) :144–152.
YANG Yuan-xi, LI Jin-long, WANG Ai-bing, et al. Preliminary assessment of the navigation and positioning performance of Beidou regional navigation satellite system[J]. Science China: Earth Sciences , 2014, 57 (1) :144–152. DOI:10.1007/s11430-013-4769-0 |
| [2] |
党超. 基于北斗的航天器测姿/测速技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
DANG Chao. Research on measuring the attitude/velocity of the spacecraft based on COMPASS[D]. Harbin: Harbin Engineering University, 2012. |
| [3] |
苑振国. GPS三维姿态测量系统的研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
YUAN Zhen-guo. Research on GPS three-dimensional attitude determination system[D]. Harbin: Harbin Engineering University, 2011. |
| [4] |
郑坤, 董绪荣, 刘亚涛, 等. GNSS载波相位多天线实时测姿系统的设计与实现[J]. 测绘科学技术学报 , 2014, 31 (2) :136–139.
ZHENG Kun, DONG Xu-rong, LIU Ya-tao, et al. Attitude determination with a GNSS multiple-antenna system[J]. Journal of Geomatics Science and Technology , 2014, 31 (2) :136–139. |
| [5] | PRATAP M, PER E. Global positioning system: signals, measurements, and performance[M]. Beijing: Publishing House of Electronics Industry, 2008 : 188 -192. |
| [6] |
陈玉林. 利用GPS载波相位信号确定载体姿态研究[D]. 南京: 南京航空航天大学, 2005: 26-27.
CHEN Yu-lin. Study on attitude determination of kinematical carrier using carrier phase of GPS system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005: 26-27. |
| [7] |
靳文瑞, 翟传润, 战兴群, 等. 基于模糊度函数法的舰船航向测量方法[J]. 中国造船 , 2008, 49 (S1) :145–151.
JIN Wen-rui, ZHAI Chuan-run, ZHAN Xing-qun, et al. Ship heading determination approach based on ambiguity function method[J]. Shipbuilding of China , 2008, 49 (S1) :145–151. |
| [8] |
韩绍伟. 附加约束条件的模糊度函数法及其在GPS相位差分动态定位中的应用[J]. 武汉测绘科技大学学报 , 1994, 19 (1) :7–14.
HAN Shao-wei. Ambiguity function method with constrained conditions and its application in GPS kinematic positioning[J]. Journal of Wuhan Technical University of Surveying and Mapping , 1994, 19 (1) :7–14. |
| [9] |
赵姣姣, 曲江华, 袁洪. 一种基于位置域的北斗快速整周模糊度确定方法[J]. 测绘科学技术学报 , 2014, 31 (3) :249–252.
ZHAO Jiao-jiao, QU Jiang-hua, YUAN Hong. A rapid integer ambiguity resolution method based on position domain of Beidou[J]. Journal of Geomatics Science and Technology , 2014, 31 (3) :249–252. |
| [10] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system[J]. GPS Solutions , 2013, 17 (2) :211–222. DOI:10.1007/s10291-012-0272-x |
 2016, Vol. 38
2016, Vol. 38
