当水下航行器与液体相对高速运动时, 航行器表面附近的液体因低压而发生相变, 即物体表面水的压强降低, 且速度越高, 压强越低。当水压降低到水的饱和蒸汽压强(2 350 Pa)以下时, 物体表面的水产生汽化现象, 形成薄的包含水汽的包络, 这便是空泡。根据文献[1-3]可知, 随着航行器速度越来越大或者人工通气量的增大, 空泡的发展过程是由局部空泡发展为超空泡、自然空泡发展为通气空泡。另外, 根据航行器速度和空泡流场中的压差的变化, 其边界有脉动存在, 从而形成非定常超空泡; 当空泡流场中压力不变时, 且沿自由边界速度恒定, 形状基本稳定形成定常超空泡[1]。
超高速航行器正是利用超空泡产生的原理和特性以及本身结构设计特点, 在水下航行过程中生成大小、长度、闭合位置等满足航行器运动稳定要求的超空泡, 使航行器表面的大部分与水隔开, 减小了航行器表面与水之间的粘性摩擦损失, 从而大大减小航行阻力, 获得难以想象的水中高速。
在实际工程应用中, 人工通气超空泡的形成及稳定是一个涉及因素很多、研究难度很大、实现困难等复杂问题。本文主要开展人工通气超空泡的数学仿真研究。根据所建立的数学模型, 分析影响超空泡形态的因素, 在给定的速度变化规律下, 改变通气参数和运动参数进行空泡形成过程的数学仿真模拟。并结合视景演示系统测试超空泡包络动态形成和超高速航行器运动过程。
1 超空泡产生机理及数学模型 1.1 超空泡产生机理由描述流场压力特性的伯努力方程可知, 当物体在水下运动时, 物体表面所受到的水压力降低, 速度越快压力越小, 然而当压力降至水的饱和蒸汽压 2 350 Pa(20 ℃ 时)以下时, 由于水的表面扩张力的作用, 物体表面的水产生汽化现象, 这便形成空泡。根据文献[5-6]可知, 通过人工通气, 空泡长度就会增大, 当与物体长度相当或将雷体包裹时, 就形成了超空泡。其形成过程如图 1 所示。
|
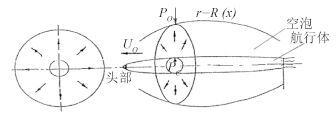
图 1 超空泡的产生机理 Fig. 1 Sketch of generation mechanism for supercavitation |
图 1 中, 当一个轴对称细长水下航行器向前运动时, 推开无运动(静止)的流体, 流体沿横剖面扩展, 随着流体向外扩展, 空泡在外部压力 P0 和内部压力 Pc 的形成压差作用下扩展开来, 随着航行器向前运动, 就不断推开无运动的流体, 不断产生流体和空泡的径向扩展, 从而形成 r = R(x)空泡流场的连续边界, 于是空泡外形就这样确定了, 并具有一定的大小和形状。
从图 1 可看出, 对于轴对称细长航行体, 生成的空泡形态基本上是椭圆形, 在横剖面上则认为空泡形状是一个圆。
对于轴对称细长航行器所生成的理想超空泡具有以下特性:
1) 空泡外形具有确定性, 只与雷体头部(空化器)大小和空泡数有关;
2) 空泡大部分长度上具有平滑清晰的边界, 内部透明, 空泡壁是光滑的, 厚度可认为等于 0;
3) 自然超空泡虽然不稳定, 但可向内部充气形成更大稳定可控的超空泡;
4) 受攻角和空化器舵角的影响, 超空泡轴会发生偏移。
根据超空泡的上述特点, 可以生成长度、大小及闭合位置均满足要求的超空泡, 从而达到水下航行器减阻的目的。
1.2 数学模型针对轴对称的通气超空泡进行数学描述。根据文献[7]可给出细长航行体所形成的超空泡的有关数学模型。
| $\frac{{{\partial ^2}S\left( {\tau ,t} \right)}}{{\partial {t^2}}} = - \frac{{{k_1}\Delta p\left( {\tau ,t} \right)}}{\rho }{\rm{,}}$ | (1) |
其中:
| $\Delta p(\tau ,t) = p(\infty ) - {p_c}(t){\rm{, }}$ | (2) |
方程的积分初始条件如下(t = τ):
| ${\dot S_0}(\tau ,t) = \frac{{{k_1}A}}{4}{D_n}{V_n}(\tau )\sqrt {{C_{x0}}} ,{S_0}(\tau ,t) = \frac{{\pi {D_n}^2}}{4}$ | (3) |
式中:t 为时间; τ 为某截面 ξ 形成的时间; S(τ, t)为截面 ξ 在 t 时刻的横截面积; Vn(τ)为生成截面 ξ 时空化器的瞬时速度; p(∞)为环境压力; Dn 为空化器直径; pc(t)为非定常通气空泡内压力 。
| $\begin{aligned} {p_c}({t_2}) \!=\! & f({t_1}, {t_2}, Q({t_1}), Q({t_2}), \\ & {\dot Q_{in}}({t_2}), {\dot Q_{out}}({t_2}), {P_c}({t_1}), p(\infty ))\text{。} \end{aligned}$ | (4) |
式中:
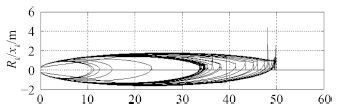
在假设的仿真条件下, 结合超高速航行器的应用需求, 根据空泡内气体模型及超空泡形态模型进行数学仿真计算。通气超空泡仿真变化曲线如图 2 所示。
|
图 2 通气超空泡变化曲线 Fig. 2 Change curve of supercavitation |
为了演示超空泡包络动态形成和超高速航行器运动过程, 本文应用 Multigen Creator 等视景开发工具创建了效果逼真、纹理清晰的水下航行器、发射舰艇及攻击目标等三维模型, 以发射舰艇装载发射超高速航行器的仿真过程, 采用 VegaPrime 构建三维战场环境, 在此基础上设计实现了超空泡数学仿真应用的视景系统。该视景系统通过实时光纤网络和以太网络两种链路方式接收来自数学或半实物仿真系统的网络数据, 驱动三维实体在立体视场中展现水下航行器和目标追踪对抗全过程, 重点实现系统中超空泡数学建模, 通过实时仿真数据在线驱动视景动态生成包络、航行器高速运行轨迹和“空泡+航行器”的相对运动关系等关键技术。视景演示系统研制的技术要求如下:
1) 模型要求(发射艇模型、水下航行器实体模型、海洋环境模型等);
2) 视频效果要求(海底、海面、雷体动作变化、水下航行器航迹等);
3) 接口要求(硬件接口、数据接口、通讯协议等);
4) 显示要求(三维动画视窗、二维动画视窗、运动参数视窗等);
5) 运行环境要求(软件平台、硬件平台等)。
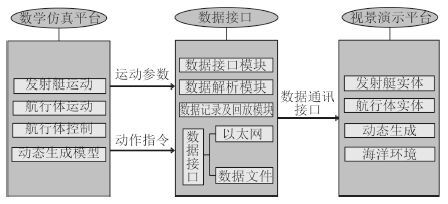
根据这些要求, 选取 AdvantageGP 软件环境作为开发平台, 在 AdvantageGP 软件环境下运用 Matlab/ Simulink 开发超空泡动态数学模型和超高速水下航行器全弹道数学模型, 以及在 AdvantageGP 软件环境下以太网的驱动程序, 然后通过规定的接口协议, 用数学仿真平台实时解算的数据通过数据接口去驱动视景演示平台, 实现超高速航行器全弹道运动过程中的弹道轨迹和超空泡动态生成过程, 其视景仿真演示系统平台构成如图 3 所示。
|
图 3 视景仿真演示系统 Fig. 3 Demonstration system of visual simulation |
为了验证超空泡实时生成效果和超高速航行器姿态控制原理和控制方法的可行性和可操作性, 以及检验水下航行器运动过程中的动作时序和完成功能的正确性, 利用图 3 的仿真系统视景演示平台, 对超空泡生成过程进行测试, 相应的视景测试效果如图 4~图 6 所示。

|
图 4 自然空泡生成效果图 Fig. 4 Effect diagram of natural cavity |

|
图 5 充气空泡生成效果图 Fig. 5 Effect diagram of ventilated cavity |

|
图 6 空泡稳定闭合状态效果图 Fig. 6 Effect diagram of closure of stability supercavitation |
1) 超空泡仿真视景演示系统设计正确, 功能完备, 能正确反映超空泡包络动态运动和超高速航行器运动过程各种动作功能;
2) 超高速航行器姿态控制数学仿真演示系统能够模拟 200 kn 超高速水下航行器全弹道运动过程, 且所计算的主要运动参数符合要求;
3) 在 AdvantageGP 软件环境下, 能够正确解算 Matlab/Simulink 的超高速航行器全弹道数学模型和超空泡动态数学模型, 通过规定的接口协议能够实时驱动超高速航行器的弹道轨迹和超空泡动态生成过程。
4 结语本文从超空泡生成机理出发, 主要描述了超空泡形态的数学模型, 进行仿真计算, 得到了不同影响因素作用下, 超空泡形态的变化规律, 进一步认识了超空泡的动态特性。在研究超空泡技术的应用方面, 通过视景系统演示平台接收的实时解算数据, 驱动三维实体模型和空泡模型动态运动, 能够逼真的演示三维战场环境。该仿真演示系统可以作为研究超空泡运动过程中各种功能、性能、指标、运动参数、充气参数、动作时序等的软件平台, 并可为进一步开展超高速航行器控制系统相关工作研究提供参考。
| [1] | SAVCHENKO Y N. Supercavitation-problems and perspectives[C]//Proceedings of the Fourth International Symposium on Cavitation. Pasadena: California Institute of Technology, 2001. |
| [2] | LOGVINOVICH G V. Hydrodynamics of flows with free boundaries[M]. Kyiv: Naukova Dumka, 1969 . |
| [3] | EUTENEUER E A. Further studies into the dynamics of a supercavitating torpedo[D]. Minneapolis: University of Minnesota, 2003. |
| [4] | VANEK B, BOKOR J, BALAS G. Theoretical aspects of high-speed supercavitation vehicle control[C]//Proceedings of the 2006 American Control Conference. Minneapolis, Minnesota, USA: IEEE, 2006. |
| [5] | GOEL A. Control strategies for supercavitating vehicles[D]. Florida: University of Florida, 2002. http://cn.bing.com/academic/profile?id=2189087011&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | GOEL A. Robust control of supercavitating vehicles in the presence of dynamic and uncertain cavity[D]. Florida: University of Florida, 2005. |
| [7] | VLASENKO Y D. Experimental investigation of supercavitation flow regimes at subsonic and transonic speeds[C]//Proceedings of the Fifth International Symposium on Cavitation (CAV2003). Osaka, Japan, 2003. |
| [8] |
褚彦军, 康凤举, 聂卫东, 等. 水下航行器对抗视景仿真系统研究[J]. 舰船电子工程 , 2004, 24 (5) :18–21.
CHU Yan-jun, KANG Feng-ju, NIE Wei-dong, et al. Research and development of visual scene simulation system in underwater vehicle distributed interactive simulation system[J]. Ship Electronic Engineering , 2004, 24 (5) :18–21. |
 2016, Vol. 38
2016, Vol. 38
