2. 海军工程大学 动力工程学院,湖北 武汉 430033
2. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China
目前国外巡洋舰、驱逐舰等大中型船舶很多都采用三机两轴和四机两轴 CCG 传动形式,这 2 种分轴传动装置均采用外齿传动的横接齿轮箱将两舷的主齿轮箱连接在一起,可以在燃汽轮机效率较佳时实现单机驱动双桨或双机驱动双桨的巡航工况。横接齿轮箱中支撑惰轮轴的轴承采用的是滑动轴承。惰轮轴承在高速、重载工况下运行,并且在齿轮箱工况转换时,由于横接齿轮的主从动关系变化会导致惰轮轴承承载情况发生变化,这种恶劣的工作条件使轴承极易出现故障。因此有必要研究高速重载工况下运行的惰轮轴承性能,以推进横接齿轮传动设计技术研究。
1 基本方程及求解过程 1.1 雷诺方程静态载荷时,油叶轴承雷诺方程的无量纲形式为[1]:
| $\begin{align} & \frac{\partial }{\partial \Phi }\left( \frac{{{{\bar{h}}}_{i}}^{3}}{{{{\bar{\mu }}}_{i}}{{R}_{x}}}\frac{\partial {{{\bar{p}}}_{i}}}{\partial \Phi } \right)+{{(\frac{R}{L})}^{2}}\frac{\partial }{\partial \lambda }\left( \frac{{{{\bar{h}}}_{i}}^{3}}{{{{\bar{\mu }}}_{i}}{{R}_{z}}}\frac{\partial {{{\bar{p}}}_{i}}}{\partial \lambda } \right)= \\ & -6{{\varepsilon }_{im}}\sin (-\theta (z)). \\ \end{align}$ | (1) |
式中:p 为油膜压力;R 为轴颈半径;L 为轴承宽度;εim 为油叶偏心率;Rx 和 Rz 为紊流因子;
雷诺方程的边界条件[2]:
| $\left. \begin{align} &\lambda =0,1{{{\bar{p}}}_{i}}=0 \\ &\phi ={{\gamma }_{i}}-\frac{\beta }{2};\phi ={{\gamma }_{i}}+\frac{\beta }{2}\ (bbh\lambda =0,1){{{\bar{p}}}_{i}}={{{\bar{p}}}_{0}} \\ &({{\gamma }_{i}}-\frac{\beta }{2})<\phi <({{\gamma }_{i}}+\frac{\beta }{2})(\lambda \ne 0,1)\ {{{\bar{p}}}_{i}}={{{\bar{p}}}_{i}}(\phi ,\lambda ) \\ \end{align} \right\}$ |
式中:β 为油叶有效张角;γi 为由 Y 轴沿轴颈方向到第 i 个油叶中心线的夹角。
当
层流条件下的能量方程无量纲形式[1]:
| $\begin{align} & ({{{\bar{h}}}_{i}}-\frac{{{{\bar{h}}}_{i}}^{3}}{6{{{\bar{\mu }}}_{i}}{{R}_{x}}}\frac{\partial {{{\bar{p}}}_{i}}}{\partial \phi })\frac{\partial {{{\bar{T}}}_{i}}}{\partial \phi }-{{(\frac{D}{L})}^{2}}\frac{{{{\bar{h}}}_{i}}^{3}}{6{{{\bar{\mu }}}_{i}}{{R}_{Z}}}\frac{\partial {{{\bar{p}}}_{i}}}{\partial \lambda }\frac{\partial {{{\bar{T}}}_{i}}}{\partial \lambda }= \\ & K\frac{{{{\bar{\mu }}}_{i}}}{{{{\bar{h}}}_{i}}}(1+\frac{{{{\bar{h}}}_{i}}^{4}}{12{{{\bar{\mu }}}_{i}}^{2}}({{(\frac{\partial {{{\bar{p}}}_{i}}}{\partial \phi })}^{2}}+{{(\frac{D}{L})}^{2}}{{(\frac{\partial {{{\bar{p}}}_{i}}}{\partial \lambda })}^{2}})). \\ \end{align}$ | (2) |
紊流条件下的能量方程无量纲形式[1]:
| $\begin{align} & ({{{\bar{h}}}_{i}}-\frac{{{{\bar{h}}}_{i}}^{3}}{6{{{\bar{\mu }}}_{i}}}\frac{\partial {{{\bar{p}}}_{i}}}{\partial \phi })\frac{\partial {{{\bar{T}}}_{i}}}{\partial \phi }-{{(\frac{D}{L})}^{2}}\frac{{{{\bar{h}}}_{i}}^{3}}{6{{{\bar{\mu }}}_{i}}}\frac{\partial {{{\bar{p}}}_{i}}}{\partial \lambda }\frac{\partial {{{\bar{T}}}_{i}}}{\partial \lambda }= \\ & \frac{{{R}_{ec}}}{2}{{C}_{f}}+\frac{{{{\bar{h}}}_{i}}^{3}}{12{{{\bar{\mu }}}_{i}}{{R}_{X}}}{{(\frac{\partial {{{\bar{p}}}_{i}}}{\partial \phi })}^{2}}+\frac{{{{\bar{h}}}_{i}}^{3}}{12{{{\bar{\mu }}}_{i}}{{R}_{Z}}}{{(\frac{D}{L})}^{2}}(\frac{\partial {{{\bar{p}}}_{i}}}{\partial {{\lambda }^{2}}}). \\ \end{align}$ | (3) |
式中:
能量方程的边界条件为:润滑剂入口处的一排节点温度为供油温度。求解时以此作为初值,应用步进方法求解温度场。
1.3 温粘方程用指数函数的形式列出温粘方程来近似地替代温粘关系。温粘方程无量纲形式为:
| ${\overline \mu _i} = {A_{}}{e^{ - B{{\overline T }_i}}}.$ | (4) |
式中:A 和 B 为温粘方程的待定系数,用最小二乘法计算。
1.4 基本方程求解过程用有限差分法求解雷诺方程[3],采用上述的雷诺边界条件计算压力。对于不同的求解区域采用不同的差分格式,压力差分方程组采用超松弛迭代法(SOR),从而解得整个求解区域的压力分布。
能量方程的求解同样采用有限差分方法[3],将雷诺方程解得的压力分布代入到能量方程解得温度分布,将温度值代入到温粘方程求解各点滑油粘度,再将粘度值代入雷诺方程,解得压力分布,如此反复迭代达到要求精度为止。
按上述方法,即由雷诺方程、能量方程与温粘方程联立求解,可求得各油叶的压力分布、温度分布及粘度分布,从而求得静态特性分布。
2 平行轴横接齿轮传动惰轮轴承性能分析平行轴横接齿轮传动惰轮轴承在正常工作时是在高速、重载工况下运行的,本文分别利用式(1)~式(4)求解惰轮轴承在不同工况下的油膜厚度、油膜压力及油膜温度等性能参数并对其进行对比分析,并且通过轴承计算判据来判定惰轮轴承所能承受的最大比压。
2.1 确定轴承计算判据1)最小油膜厚度:hmin ≥ 0.015 mm。
2)油膜最高温度:经过大量试验,确定巴氏合金所能承受的最高温度,考虑程序计算误差后,油膜最高温度 tmax ≤ 110 ℃。
2.2 高速下惰轮轴承性能确定高线速度工况的线速度范围:以三机两轴和四机两轴 CCG 传动方案设计参数为参考,高线速度工况中线速度范围约为 40 m/s ≤ V ≤ 100.5 m/s。进行大量的轴承性能计算(满足轴承判据),得出高线速度下的惰轮轴承性能参数如表 1 所示。
|
|
表 1 高线速度下的惰轮轴承性能参数表 Tab.1 Performance parameters of idler shaft under high speed |
由表 1 可见,惰轮轴承在高线速度工况下运行时,载荷增大时,最小油膜厚度随之减小,功耗随之增大,供油流量随之增大,油膜最高温度随之增大,但各轴承性能参数变化量较小,说明在线速度一定时,载荷的变化对轴承性能的影响较小。
经计算,该惰轮轴承在线速度 100.5 m/s、比压 2.19 MPa 工况下运行时,油膜温度达到巴氏合金许用最大值,所以该惰轮轴承能承受的最大线速度为 100.5 m/s。此时惰轮轴承的性能(中截面处)如图 1 和图 2 所示:
|
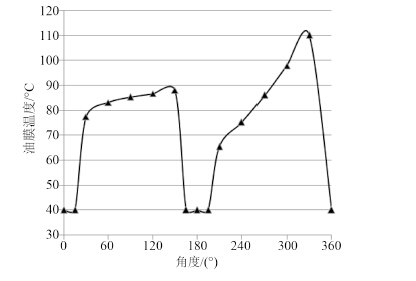
图 1 惰轮轴承轴对称处油膜温度分布曲线图 Fig. 1 Distribution of oil slick temperature near the axial symmetry areas of idler shaft |

|
图 2 惰轮轴承轴对称处油膜压力分布曲线图 Fig. 2 Distribution of oil slick pressure near the axial symmetry areas of idler shaft |
从图 1 可看出,轴承温度在 0° 处为 40 ℃,为进油温度。迅速上升到 87.9 ℃,此时的圆周角度为 150°,然后迅速下降至 40 ℃。在进油口处温度保持 40 ℃ 不变,离开出油口则油膜温度迅速上升至 110 ℃,此时的圆周角度为 330°,然后迅速下降至 40 ℃。
从图 2 中可看出,轴承油膜压力约从 210° 开始快速上升,在 270° 达到最大油膜压力 17.3 MPa,然后快速下降,约在 345° 时停止下降(进入油槽)。从油膜压力分布图中可看出,在该高速工况下,此惰轮轴承最大油膜压力为 17.3 MPa,没有超出轴承材料的许用应力,滑动轴承可以正常工作。
2.3 重载下惰轮轴承性能确定高比压工况的线速度范围:以三机两轴和四机两轴 CCG 传动方案设计参数为参考,经过大量轴承性能计算(满足轴承判据),得到惰轮轴承高比压工况的比压范围为 3.0 MPa ≤ p ≤ 4.58 MPa,并得出高比压下的惰轮轴承性能参数表(见表 2)。
|
|
表 2 高比压下的惰轮轴承性能参数表 Tab.2 Performance parameters of idler shaft under high specific pressure |
由于惰轮轴承在高比压工况下运行时,油膜容易破裂,线速度可变化范围较小,各轴承性能参数变化不明显,所以分析惰轮轴承各性能参数的变化规律时,采用轴承运行在 3.99 MPa 比压工况下进行分析,并且给出了该惰轮轴承在承受最大比压 4.58 MPa 时的性能参数(此时惰轮轴承的最小油膜厚度和最高温度均接近许用最小油膜厚度)。
由表 2 可见,惰轮轴承在高比压工况下运行,线速度增大时,最小油膜厚度随之增大,功耗随之增大,供油流量随之增大,油膜最高温度随之增大,各轴承性能参数变化量较大,说明在比压一定时,线速度的变化对轴承性能的影响较大。此时惰轮轴承的性能(中截面处)如图 3 和图 4 所示。
|
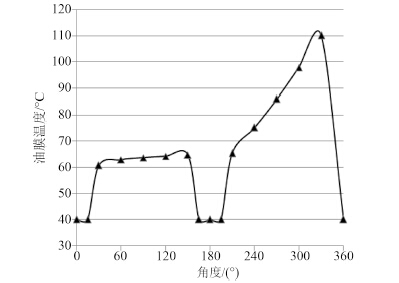
图 3 惰轮轴承轴对称处油膜温度分布曲线图 Fig. 3 Distribution of oil slick temperature near the axial symmetry areas of idler shaft |

|
图 4 惰轮轴承轴对称处油膜压力分布曲线图 Fig. 4 Distribution of oil slick pressure near the axial symmetry areas of idler shaft |
从图 3 可看出,轴承温度在 0 角度处为 40 ℃,为进油温度。缓慢上升到 64.7 ℃,此时的圆周角度为 150°,然后迅速下降至 40 ℃。在进油口处温度保持 40 ℃ 不变,离开进油口则油膜温度迅速上升,在另一个进油口处温度停止上升至 110 ℃,此时的圆周角度为 330°。从图 4 可看出,轴承油膜压力约从 210° 开始快速上升,在 270° 达到最大油膜压力 29.8 MPa,然后快速下降,约在 345° 时停止下降(进入油槽)。从油膜压力分布图中可看出,在该高速工况下,此惰轮轴承最大油膜压力为 29.8 MPa,没有超出轴承材料的许用应力,滑动轴承可以正常工作。
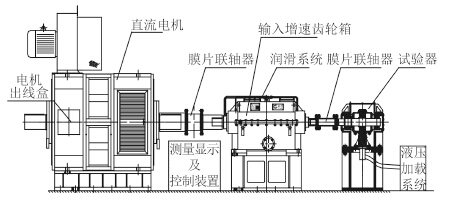
3 试验验证在滑动轴承可靠性试验台上对惰轮轴承进行验证试验,试验台由直流电机、输入增速齿轮箱、膜片联轴器、试验器、液压加载系统、润滑系统、测量显示及控制装置组成,通过控制直流电机转速实现线速度的控制,通过控制液压加载系统实现试验件比压的控制,试验台组成如图 5 所示。
|
图 5 滑动轴承可靠性试验台 Fig. 5 Platform for testing the reliability of sliding bearing |
在惰轮轴承试验件中截面轴向方向两侧分别设温度测点和压力测点,截面圆周方向每隔 30° 均布测点位置,对试验件高速工况(线速度 100.5 m/s、比压 2.19 MPa)、重载工况(线速度 15.08 m/s、比压 4.58 MPa)进行验证试验,得到惰轮轴承的性能参数试验数据。
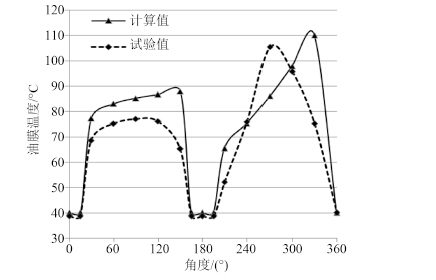
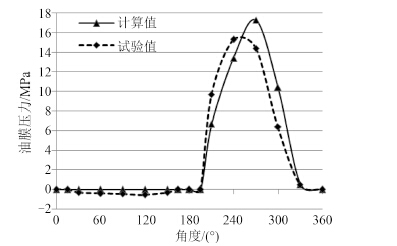
由图 6 和图 7 可知,惰轮轴承在高速工况下运行时,油膜温度与油膜压力试验值的变化趋势与理论计算值大致相同,且油膜最高温度试验值为 105.4 ℃,计算值误差为 4.7%。油膜最高压力试验值为 15.3 MPa,计算值误差为 13.1%。
|
图 6 惰轮轴承(高速)油膜温度理论与试验对比 Fig. 6 Comparison of oil slick temperature between theoretical and testing results(high speed) |
|
图 7 惰轮轴承(高速)油膜压力理论与试验对比 Fig. 7 Comparison of oil slick pressure between theoretical and testing results(high speed) |
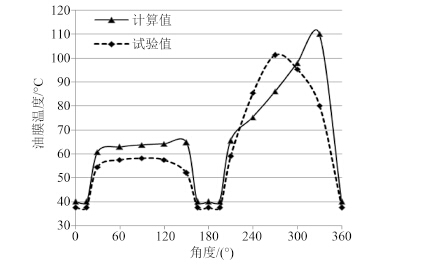
由图 8 和图 9 可以,惰轮轴承在重载速工况下运行时,油膜温度与油膜压力试验值的变化趋势与理论计算值大致相同,且油膜最高温度试验值为 101.2 ℃,计算值误差为 8.7%。油膜最高压力试验值为 26.5 MPa,计算值误差为 12.5%。
|
图 8 惰轮轴承(重载)油膜温度理论与试验对比 Fig. 8 Comparison of oil slick temperature between theoretical and testing results(heavy load) |
本文以三机两轴和四机两轴 CCG 传动设计参数为参考,对平行轴横接齿轮传动惰轮轴承进行了性能进行了理论计算和实验验证,研究了惰轮轴承在高速、重载工况下的性能参数分布及轴承线速度、比压变化对轴承性能参数的影响,计算了算例中惰轮轴承所能承受的最大线速度及最大比压,为高参数惰轮轴承的设计提供了理论依据。并得出了以下结论:
1)在线速度一定时,载荷的变化对轴承性能的影响较小;
2)在比压一定时,线速度的变化对轴承性能的影响较大;
3)计算得出惰轮轴承所能承受的最大比压为 4.58 MPa,经过试验验证重载工况下,理论值与试验值变化趋势大致相同,轴承性能参数最大计算误差为 13.1%;
4)计算得出惰轮轴承所能承受的最大线速度为 100.5 m/s,经过试验验证高速工况下,理论值与试验值变化趋势大致相同,轴承性能参数最大计算误差为 12.5%。
| [1] | 张直明, 张言羊, 谢友柏. 滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社, 1986 . |
| [2] | 陈伯贤, 裘祖干, 张慧生. 流体润滑理论及其应用[M]. 北京: 机械工业出版社, 1991 . |
| [3] | 温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2002 . |
 2016, Vol. 38
2016, Vol. 38
