船舶吃水在船舶进出港、过浅滩、系靠码头和装卸货物时起着极其重要的作用[1]。它是衡量船舶安全性的重要指标,是计算船舶富余水深及净空高度的基础。目前大副进行货物预配载时,会根据船舶装载手册或船舶配载仪计算出船舶的当前浮态,即船舶首吃水、尾吃水及横倾角[2-6]。然而船员更关心的是当前载况下船舶的六面吃水。由于船舶首尾垂线和船舶六面水尺纵向位置的不同,相同载况下其吃水读数会有不同,就需要一种由船舶首尾吃水计算船舶六面吃水的方法。
本文基于船舶外壳三维 STL 模型和计算机图形学的 S-H 多边形剪裁算法,探讨一种由船舶首尾吃水计算船舶六面吃水的方法,该方法计算精度较高,通用性较好。
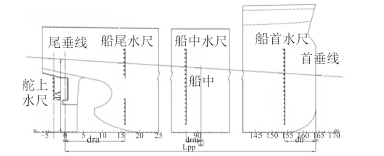
1 船舶吃水在船舶实际营运过程中经常用到的吃水为船舶首尾吃水及六面吃水。首尾垂线吃水是指船舶首尾垂线处的吃水。通常描述船舶浮态的首吃水、尾吃水及吃水差就是指船舶首尾垂线吃水。六面吃水船舶水尺刻划于船体两舷侧,用于计量船舶装载量的特殊标尺,船舶水尺由直线和数字两部分构成,是观测和计量船舶载货和配载的依据,通常位于船尾、船中及船首两侧船壳。然而为了提高水尺精度和读取水尺读数方便,船舶设计部门经常将船舶尾部水尺分为两部分,一部分在船舶舵上绘制,一部分在船舶尾部绘制,如图 1 所示为 25 万吨矿砂船六面水尺示意图。
|
图 1 船舶首尾吃水及六面吃水 Fig. 1 Ship’s fore and after drafts and six drafts |
从图 1 中可知,船舶首尾垂线所在的纵向位置和船舶首尾水尺并不相同,所以船舶首尾水尺和船舶六面水尺的读数并不相同。
2 船舶 STL 模型STL(STereo Lithography)文件是一种 3D 模型文件格式,是 3D SYSTEM 公司于 1988 年制定的一个接口协议。它是一种为快速原型制造技术服务的三维图形文件格式,在科学计算可视化、计算机动画、3D 打印、虚拟现实及快速成形等领域中应用广泛。其无序地列出了构成实体表面的所有三角形面片的信息,包括三角形各个定点的三维坐标及三角形面片的法矢量,可以简单认为是将曲面三角化的结果。
图 2 给出 6.4 万散货船“SPRING COSMOS”外壳及所有舱室的 STL 模型,图 3 所示为 5.6 万散货船“太行 128”的 STL 模型,其来源于船舶设计软件 NAPA,是船舶的真实设计数据[6],数据可靠性好。

|
图 2 64 K 散货船“Spring Cosmos”的 STL 模型 Fig. 2 STL model of 64 K bulk carrier “Spring Cosmos” |

|
图 3 56 K 散货船“太行 128”的 STL 模型 Fig. 3 STL model of bulk carrier “Taihang 128” |
已知船舶首尾吃水计算六面吃水的基本步骤如下:
1)用各个水尺所在的纵剖面切割船舶外壳STL模型,获得船首、船中计船尾水尺的封闭多边形。
2)由船舶首尾吃水及横倾角可得到倾斜水线面的方程。
3)船舶水尺所在的剖面和倾斜水线面求交,得到水线部分的多边形,交点的垂向坐标即为六面水尺读数。
3.1 水尺剖面的确定船舶各个水尺所在剖面的肋位号及纵向坐标可以从船舶设计部门提供的船舶装载手册中查询得来。以 25 万散货“Shandong Renhe”为例:舵上的水尺肋位号 -3#(-2.7 m)、船尾水尺肋位号 16#(14.4 m)、船中水尺肋位号 89#(156.15 m)及船首水尺肋位号 154#(312 m)。用水尺所在肋位所确定的纵剖面去切割船舶外壳的 STL 模型即可获得各个水尺的封闭多边形,如图 4 所示。

|
图 4 水尺剖面切割外壳 STL 模型 Fig. 4 STL model of ship hull |
图 5 为切割完成后得到的各个水尺的封闭多边形。在切割 STL 模型时,用到的主要关键技术有:STL 模型数据解析[7-8]、空间三角形和空间平面求交[9]、截面轮廓提取及截面轮廓的三角化[10-16]。

|
图 5 各个水尺剖面 Fig. 5 The draft section |
本文采用文献[17-20]提出的船体坐标系和固定坐标系,从固定坐标系 ox'y'z' 到船体坐标系 oxyz 的坐标变换矩阵为:
| $B_{ox'y'z'}^{oxyz} \!=\! \left(\!\!\! {\begin{array}{*{20}{c}} {\cos \alpha /\cos \theta } & 0 & {\! - \tan \varphi \cos \alpha }\\ { - \sin \theta \tan \varphi \cos \alpha } & {\cos \theta } & { - \tan \theta \cos \alpha }\\ {\cos \theta \tan \varphi \cos \alpha } & {\sin \theta } & {\cos \alpha } \end{array}} \!\!\!\right).$ |
式中:θ 为船舶横倾角;φ 为船舶纵倾角;α 为倾斜角,即倾斜水线面与基准面之间的夹角
在固定坐标系下水平面的法矢量 n =(0,0,1),则在船体坐标系下水线面的法矢量为:
| $n' = B_{ox'y'z'}^{oxyz}\left[{\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right] = \left[{\begin{array}{*{20}{c}} { - \tan \varphi \cos \alpha }\\ { - \tan \theta \cos \alpha }\\ {\cos \alpha } \end{array}} \right] = \left[{\begin{array}{*{20}{c}} { - \tan \varphi }\\ { - \tan \theta }\\ 1 \end{array}} \right].$ |
倾斜水线面过船中吃水点(0,0,Tm),即可得到倾斜水线面的一般式方程:
| $ \tan \varphi \cdot x + \tan \theta \cdot y - z - {T_m} = 0.$ |
S-H(Sutherland-Hodgman)算法也叫逐边裁剪法,该算法由萨瑟兰德(I.E.Sutherland)和霍德曼(Hodgman)在 1974 年提出。这种算法采用了分割处理、逐边裁剪的思想,是一种剪裁多边形区的高效算法。其总体策略是顺序的将每一多边形的一对顶点送给一组裁剪器(左、右、下、上)。一个裁剪器完成对一对顶点的处理后,该边留下的坐标值立即送给下一个剪裁器,最终输出的是一个完整的多边形填充区边界的顶点队列。
在用裁剪边界对多边形的边裁剪时有以下 4 种情况需要考虑:
1)多边形边的第一端点在裁剪边界外部而第二端点在内部;
2)2 个端点都在剪裁边界内部;
3)是第一端点在边界内部而第二端点在边界外部;
4)2 个端点都在裁减边界外部。这 4 种情况的输出点情况如图 6 所示:情况 1 输出交点和终点;情况 2 输出终点;情况 3 输出交点;情况 4 无交点输出。

|
图 6 S-H 多边形剪裁算法 Fig. 6 S-H polygon clipping algorithms |
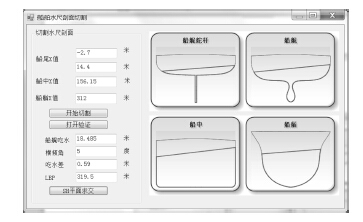
图 7 所示为 25 万吨矿石船“Shandong Ren He”某一载况下,采用 S-H 剪裁算法进行求交计算的实验结果,图 7 中部分为各个水尺剖面与倾斜水线面求交得到水下部分的封闭多边形,其交点垂向坐标即为水尺读数。
|
图 7 S-H 剪裁算法计算交点 Fig. 7 Intersection points computed by S-H clipping algorithms |
本文基于 VS2013 平台,采用 C# 编程语言编制了船舶吃水转换程序。以 25 万吨矿砂船“Shandong Ren He”及 6.4 万吨散货船“Spring Cosmos”进行了实例计算,和船舶设计软件 NAPA 计算结果相比,误差较小。如表 1 和表 2 所示。
|
|
表 1 25 万吨矿砂船船中水尺计算结果 Tab.1 Midship draft calculate result of 250 k ore carrier |
|
|
表 2 6.4 万吨散货船船中水尺计算结果 Tab.2 Midship draft calculate result of 64 k bulk carrier |
表 1 中 ,LOAD0 为空船载况,LOAD1 为压载出港载况,LOAD5 为均质货满载出港载况,LOAD18 为矿石装载载况,LOAD21 为隔舱装载载况。
表 2 中,LOAD0 为空船载况,LOAD3 为压载出港载况,LAOD8 为压载进港载况,LAOD12 为均质货满载出港载况,LOAD37 为隔舱装载工况。
分析表 1 和表 2 中数据可知,本文所述方法的计算结果和船舶设计软件 NAPA 的计算结果的绝对误差基本在 1 cm 以下,NAPA 软件的计算结果保留到了两位小数字,若本文的计算结果也保留到 2 位小数字,和 NAPA 计算结果基本没有差别,证明了本文所述方法的正确性。
5 结语本文探讨了一种基于船舶外壳三维 STL 模型及 S-H 多边形剪裁算法计算船舶六面吃水的方法,可得到如下结论:
1)船舶 STL 网格模型来源于船舶设计数据,数据来源可靠,可保证计算精度;
2)将船舶吃水转换问题转化成封闭多边形和倾斜水线面的求交问题,通过切割外壳 STL 模型得到各个水尺的封闭多边形,采用 S-H 剪裁算法处理多边形和水线面求交问题,程序通用性好,适用于各种剖面形状,包括三体船、五体船等特种船舶;
3)上述算法也可解决船检人员在水尺计重过程中船舶一侧吃水不方便读取的问题,即已知一面水尺的水尺读数和横倾角,计算出另一面的水尺读数。
文中的方法已经成功应用在研究所自主研发的散货船装载计算机系统中,计算精度较高,通用性较好,具有一定的工程实用价值。
| [1] |
盛振邦, 刘应中.
船舶原理(上册)[M]. 上海: 上海交通大学出版社, 2003 : 20 -44.
SHENG Zhen-bang, LIU Ying-zhong. Principles of ship[M]. Shanghai: Shanghai JiaoTong University Press, 2003 : 20 -44. |
| [2] |
刘辉强. 水尺计重及其误差分析[D]. 大连: 大连海事大学, 2010.
LIU Hui-qiang. Draft survey and errors analysis[D]. Dalian: Dalian Maritime University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10151-2010098382.htm |
| [3] | RAN X, SHI C J, CHEN J B, et al. Draft line detection based on image processing for ship draft survey[C]//Proceedings of the 2011 2nd International Congress on Computer Applications and Computational Science. Berlin Heidelberg: Springer, 2012: 39-44. |
| [4] | GU H W, ZHANG W, XU W H, et al. Digital measurement system for ship draft survey[J]. Applied Mechanics and Materials , 2013, 333 . |
| [5] | MAILLOT P G. A new, fast method for 2D polygon clipping: analysis and software implementation[J]. ACM Transactions on Graphics (TOG) , 1992, 11 (3) :276–290. DOI:10.1145/130881.130894 |
| [6] |
刘春雷, 张秀凤, 孙霄峰, 等. 基于加密型值表的船舶静水力特性精确计算[J]. 中国造船 , 2013, 54 (4) :163–172.
LIU Chun-lei, ZHANG Xiu-feng, SUN Xiao-feng, et al. Hydrostatic performance calculation of vessels based on densified table of offsets[J]. Shipbuilding of China , 2013, 54 (4) :163–172. |
| [7] |
纪小刚. RP系统中STL模型的分割与拼接研究[D]. 南京: 南京理工大学, 2003: 23-47.
JI Xiao-gang. Research of STL model's rectification and topology in RP system[D]. Nanjing: Nanjing University of Science and Technology, 2003: 23-47. http://cdmd.cnki.com.cn/article/cdmd-10288-2003105386.htm |
| [8] | SCHNEIDER P J. EBERLY D H. Geometric tools for computer graphics[M]. ZHOU Chang-fa, Trans. Beijing: Publishing House of Electronics Industry, 2005 : 270 -392. |
| [9] | RAPPOPORT A. An efficient algorithm for line and polygon clipping[J]. The Visual Computer , 1991, 7 (1) :19–28. DOI:10.1007/BF01994114 |
| [10] |
潘海鹏, 周天瑞, 朱根松, 等. STL模型切片轮廓数据的生成算法研究[J]. 中国机械工程 , 2007, 18 (17) :2076–2079.
PAN Hai-peng, ZHOU Tian-rui, ZHU Gen-song, et al. Research on the algorithm for generating the slicing profile of STL model[J]. China Mechanical Engineering , 2007, 18 (17) :2076–2079. |
| [11] |
金文华, 何涛, 唐卫清, 等. 简单快速的平面散乱点集凸包算法[J]. 北京航空航天大学学报 , 1999, 25 (1) :72–75.
JIN Wen-hua, HE Tao, TANG Wei-qing, et al. Simple fast convex hull algorithm of planar point set[J]. Journal of Beijing University of Aeronautics Astronautics , 1999, 25 (1) :72–75. |
| [12] |
胡德洲, 李涤尘, 洪军, 等. 快速成形制造中截面轮廓快速生成算法研究[J]. 中国机械工程 , 2001, 12 (6) :654–656.
HU De-zhou, LI Di-chen, HONG Jun, et al. Research on the algorithm for rapidly generating cross-sectional contour in rapid prototyping & manufacturing[J]. China Mechanical Engineering , 2001, 12 (6) :654–656. |
| [13] |
李学军, 黄文清. 平面区域三角化的快速算法[J]. 计算机辅助设计与图形学学报 , 2003, 15 (2) :233–238.
LI Xue-jun, HUANG Wen-qing. Fast triangulation algorithm for planar regions[J]. Journal of Computer-aided Design & Computer Graphics , 2003, 15 (2) :233–238. |
| [14] |
闵卫东, 唐泽圣. 二维任意域内点集的Delaunay三角划分的研究[J]. 计算机学报 , 1995, 18 (5) :357–364.
MIN Wei-dong, TANG Ze-sheng. The Delaunay triangulation of a point set within an arbitrary 2D domain[J]. Chinese Journal of Computers , 1995, 18 (5) :357–364. |
| [15] |
马小虎, 潘志庚, 石教英. 基于凹凸顶点判定的简单多边形Delaunay三角剖分[J]. 计算机辅助设计与图形学学报 , 1999, 11 (1) :1–3.
MA Xiao-hu, PAN Zhi-geng, SHI Jiao-ying. Delaunay triangulation of simple polygon based on determination of CONVEX-CONCAVE vertices[J]. Journal of Computer-aided Design and Computer Graphics , 1999, 11 (1) :1–3. |
| [16] |
刘少华, 汤军, 吴东胜, 等. 简单多边形三角剖分的一种快速算法及应用[J]. 计算机应用与软件 , 2008, 25 (3) :79–80.
LIU Shao-hua, TANG Jun, WU Dong-sheng, et al. A fast algorithm for simple polygon triangulation and its applications[J]. Computer Applications and Software , 2008, 25 (3) :79–80. |
| [17] |
赵晓非, 林焰. 关于解船舶浮态问题的矩阵方法[J]. 中国造船 , 1985 (3) :57–66.
ZHAO Xiao-fei, LIN Yan. Matrix methods for solving ship floating state problem[J]. Shipbuilding of China , 1985 (3) :57–66. |
| [18] |
林焰, 李铁骊, 纪卓尚. 破损船舶自由浮态计算[J]. 大连理工大学学报 , 2001, 41 (1) :85–89.
LIN Yan, LI Tie-li, JI Shang-zhuo. Ship damage floating calculation[J]. Journal of Dalian University of Technology , 2001, 41 (1) :85–89. |
| [19] |
陆丛红, 林焰, 纪卓尚. 基于曲面表达的几何特性计算及其在船舶工程中的应用[J]. 哈尔滨工程大学学报 , 2005, 26 (6) :697–703.
LU Cong-hong, LIN Yan, JI Zhuo-shang. Geometric properties calculation based on surface representation and its application to ship engineering[J]. Journal of Harbin Engineering University , 2005, 26 (6) :697–703. |
| [20] |
张明霞. 基于NURBS曲面的船舶破舱稳性计算方法研究[D]. 大连: 大连理工大学, 2002.
ZHANG Ming-xia. Study of hull damage stability calculation with NURBS technology[D]. Dalian: Dalian University of Technology, 2002. http://www.oalib.com/references/17524734 |
 2016, Vol. 38
2016, Vol. 38
