2. 海军工程大学,湖北 武汉 430033
2. Naval University of Engineering, Wuhan 430033, China
潜艇以其在海洋中的隐蔽性和机动性的特点发挥了其他舰种难以起到的作用。由于海水温度和盐度分布的不均匀性,导致了其密度的层化特性,在这样的分层流体中,内波像表面波一样存在,只要海水密度稳定分层,且有扰动源存在,内波就会产生。在海洋深处运动的潜艇在海洋表面会形成内波尾迹,可以通过星载或机载合成孔径雷达(SAR)获得这种尾迹的信息 这对发展潜体的非声探测技术非常重要。
目前,比较多的理论研究工作是基于势流理论,针对运动点源等在分层流体中的兴波问题。Keller,Munk[1]进行了分层流体中物体生成的内波尾迹的理论研究,给出了任意色散介质中运动源生成的尾流方程式和尾流的远场和近场的波形图。Miles[2]对于均匀分层和有温跃层结构的流体,研究了船体效应和尾迹塌陷效应导致的内波,指出自由面形变率参数在内波与自由面相互作用中具有重要作用。Hughes[3]研究了表面船生成的表面尾迹和内波尾迹,并提供了内波尾迹的形式。Tulin等[4]进行了超临界情况下浅跃层的船内波研究。Timour[5]将 Yeung,Nguyen[6]的两层流体模型推广至多层流体系统,利用摄动方法,分析了内波对自由面波的影响。Wei[7]则研究了在两层流体中定常运动的偶极子的兴波特性问题。朱伟[8]从 Green 定理出发,基于 Rankin 源的分层边界积分理论模型研究两层有限深流体中运动潜体的兴波特性问题。本文基于势流理论,采用 Hess-Smith 方法,对两层介质中运动潜体的内波进行数值计算研究,得到表面波和内波波形与航速、潜深之间的关系。
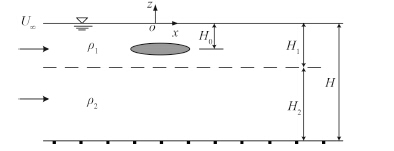
1 基本方程和边界条件及数值计算方法设海水为两层介质,上层水的密度为 ρ1,深度为 H1;下层水的密度为 ρ2,深度为 H2;总水深为 H。潜体在上层(或下层)介质中以速度 U∞ 匀速直线航行,潜体的下潜深度为 H0。将坐标系固结在匀速运动的潜体上,原点 o 位于未扰动的水面上,x 轴与潜体轴线平行,方向与潜体运动方向相反,z 轴垂直向上,在此坐标系中观察,远方流体以速度 U∞ 沿 x 方向流向潜体(见图 1)。
|
图 1 潜体在两层流体中运动示意图 Fig. 1 Sketch map of submerged body in two-layer fluid |
设流体是无粘性流体,流动无旋,则流体流动可以用势流理论求解。上、下两层流体的扰动速度势分别记为 φ1 和 φ2。则 φ1 和 φ2 满足的基本方程分别为:
| ${{\nabla }^{2}}{{\phi }_{1}}=0,\ -{{H}_{1}}+{{\zeta }_{2}}<z<{{\zeta }_{1}},$ | (1) |
| ${{\nabla }^{2}}{{\phi }_{2}}=0,\ -H<z<-{{H}_{1}}+{{\zeta }_{2}}.$ | (2) |
式中:
在定常流动和小扰动条件下,在自由面上,运动学条件为:
| $\frac{\partial {{\phi }_{1}}}{\partial z}={{U}_{\infty }}\frac{\partial {{\zeta }_{1}}}{\partial x},z=0,$ | (3) |
动力学条件为:
| ${{U}_{\infty }}\frac{\partial {{\phi }_{1}}}{\partial x}+g{{\zeta }_{1}}=0,z=0,$ | (4) |
将式(3)代入式(4)得到自由面上运动学和动力学结合条件为:
| $\frac{U_{\infty }^{2}}{g}\frac{\partial \phi _{1}^{2}}{\partial {{x}^{2}}}+\frac{\partial {{\phi }_{1}}}{\partial z}=0,{z=0},$ | (5) |
在小扰动条件下,潜艇表面上满足的边界条件为:
| $\frac{\partial {{\phi }_{1}}}{\partial x}{{n}_{x}}+\frac{\partial {{\phi }_{1}}}{\partial y}{{n}_{y}}+\frac{\partial {{\phi }_{1}}}{\partial z}{{n}_{z}}=-{{U}_{\infty }}{{n}_{x}},0<{{H}_{0}}<{{H}_{1}},$ | (6) |
| $\frac{\partial {{\phi }_{2}}}{\partial x}{{n}_{x}}+\frac{\partial {{\phi }_{2}}}{\partial y}{{n}_{y}}+\frac{\partial {{\phi }_{2}}}{\partial z}{{n}_{z}}=-{{U}_{\infty }}{{n}_{x}},{{H}_{1}}<{{H}_{0}}<{{H}_{2}},$ | (7) |
在定常流动和小扰动条件下,在分层界面上,运动学条件为:
| $\frac{\partial {{\phi }_{1}}}{\partial z}=\frac{\partial {{\phi }_{2}}}{\partial z}={{U}_{\infty }}\frac{\partial {{\zeta }_{2}}}{\partial x},z={{H}_{1}},$ | (8) |
在分层界面上,动力学边界条件为:
| ${{\rho }_{1}}{{U}_{\infty }}\frac{{{\partial }^{2}}{{\phi }_{1}}}{\partial {{x}^{2}}}+{{\rho }_{1}}g\frac{\partial {{\zeta }_{2}}}{\partial x}={{\rho }_{2}}{{U}_{\infty }}\frac{{{\partial }^{2}}{{\phi }_{2}}}{\partial {{x}^{2}}}+{{\rho }_{2}}g\frac{\partial {{\zeta }_{2}}}{\partial x}.$ | (9) |
将式(8)代入式(9)得得到分层界面上运动学和动力学结合条件为:
| ${{\rho }_{1}}(\frac{U_{\infty }^{2}}{g}\frac{{{\partial }^{2}}{{\phi }_{1}}}{\partial {{x}^{2}}}+\frac{\partial {{\phi }_{1}}}{\partial z})={{\rho }_{2}}(\frac{U_{\infty }^{2}}{g}\frac{{{\partial }^{2}}{{\phi }_{2}}}{\partial {{x}^{2}}}+\frac{\partial {{\phi }_{2}}}{\partial z}),$ | (10) |
在海底的边界条件为:
| $\frac{\partial {{\phi }_{2}}}{\partial z}=0,\ z=-H,$ | (11) |
自由面波高的计算公式为:
| ${{\zeta }_{1}}=-\frac{{{U}_{\infty }}}{g}\frac{\partial {{\phi }_{1}}}{\partial x},$ | (12) |
分层界面波高的计算公式为:
| ${{\zeta }_{2}}=-\frac{{{U}_{\infty }}}{(1-\gamma )g}\left( \frac{\partial {{\phi }_{2}}}{\partial x}-\gamma \frac{\partial {{\phi }_{1}}}{\partial x} \right),$ | (13) |
式中
采用常数密度的边界元法(Hess-Smith 方法)求解上述基本方程和边界条件。在物体表面、自由表面、分界面和水底划分四边形单元,在每个单元上分布常数密度的面源,采用 Dawson 的方法,通过两次采用迎风差分的方法[9],解出面源密度。进而计算出上层和下层流体的流动速度势和速度。根据式(12)计算自由表面波高,根据式(13)计算内波波高。
2 算例采用 C 语言开发了计算潜艇在两层分层介质中运动产生内波和表面波的边界元计算程序。潜艇或其他模型可以在上层或下层流体中运动,可以对无限水深和有限水深工况进行计算。通过命令窗口,输入相关参数后进行计算,表面波和内波波高通过条用 Matlab 计算引擎绘出。
2.1 无限水深下均匀环境椭球体兴波阻力计算验证椭球体三轴长度比为
|
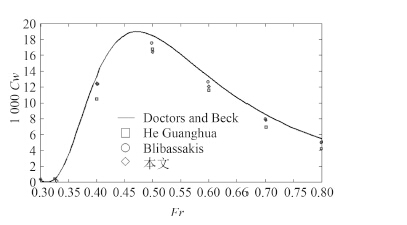
图 2 椭球体兴波阻力系数 Fig. 2 wave-making resistance coefficient of ellipsoid |
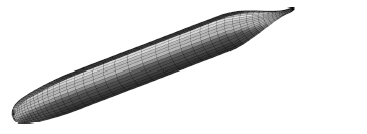
由于计算模型与 xoz 平面对称有关,只对 xoz 平面一侧表面进行离散。采用镜像法考虑另一侧的影响。半个光体表面的面元数目为 1 000 个,其中沿轴向 50 个单元,周向为 20 个单元(见图 3)。自由表面的范围取为:潜艇头部 500 m,尾部 2 000 m,侧面 800 m,自由表面一半的面元数目为 15 000 个,其中沿纵向为 300 个单元,横向为 50 个单元。所以总面元数目为 16 000 个。
|
图 3 SUBOFF 半光体表面单元 Fig. 3 Panels of half suboff bare body surface |
采用放大 20 倍 SUBOFF 光体模型,H1=45 m,H2=100 m,考虑密度比 γ=0.974 时,表面波模式的临界佛鲁德数 Fr1=0.997,内波模式的临界佛鲁德数 Fr2=0.077 4,其中,Fm 由式(14)确定。
| ${{F}_{rn}}^{2}=\frac{1}{2}+{{(-1)}^{n+1}}\sqrt{\frac{1}{4}-\frac{(1-\gamma )\times {{H}_{1}}\times {{H}_{2}}}{{{({{H}_{1}}+{{H}_{2}})}^{2}}}}.$ |
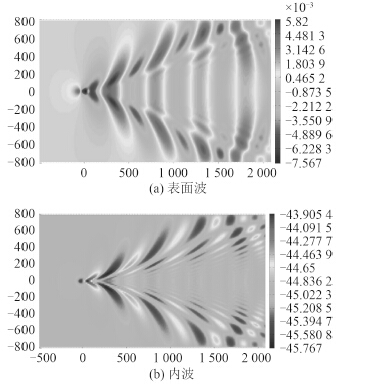
图 4~图 6 为在潜深 30 m 时,不同水深佛鲁德数情况下的表面波和内波波形。在水深佛鲁德数比较小时(见图 4),表面波和内波以横波为主,影响范围比较小;在接近内波模式的临界佛鲁德数 Fr2 时(见图 5),表面波和内波中散波和横波的波形都比较明显;在水深佛鲁德数比较大时(见图 6),表面波和内波以散波为主。

|
图 4 H0=30 m,Fh=0.034 Fig. 4 H0=30 m, Fh=0.034 |
|
图 5 H0=30 m,Fh=0.068 Fig. 5 H0=30 m, Fh=0.068 |

|
图 6 H0=30 m,Fh=0.102 Fig. 6 H0=30 m, Fh=0.102 |
图 7 为在潜深 30 m 时,不同水深佛鲁德数情况下表面波和内波波峰和波谷(图中内波数据为计算值加上 H1 的结果)。从图中可以看出,随着水深佛鲁德数的增加,表面波的波峰和波谷在增加;而内波的波峰和波谷在接近内波模式的临界佛鲁德数 Fr2 时均接近最大值,在大于 Fr2 时,内波的波峰和波谷变化趋于平缓。

|
图 7 H0=30 m,表面波和内波的波峰和波谷 Fig. 7 Peak and trough of surface wave and internal wave for H0 = 30 m |
图 8 和图 9 为 Fh=0.068(航速为 5 kn)时,不同潜深时的表面波和内波波形。结合图 5可看出,表面波和内波波形,在同一航速、不同潜深的情况下,分布是相似的,但当潜体位于下层流体时,波峰与波谷的位置刚好与潜体位于上层流体时相反。
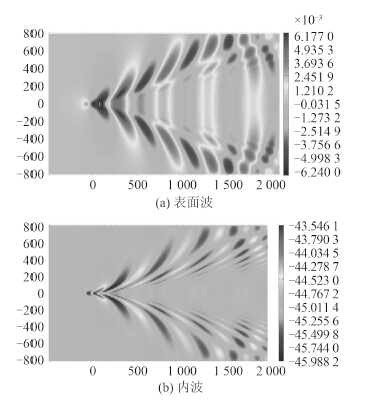
|
图 8 H0=37.5 m,Fh=0.068 表面波和内波 Fig. 8 Surface wave and internal wave for H0=60 m, Fh=0.068 |
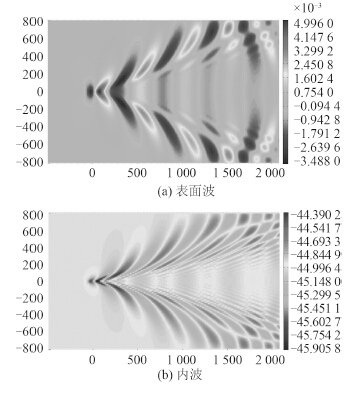
|
图 9 H0=60 m,Fh=0.068 表面波和内波 Fig. 9 Surface wave and internal wave for H0=60 m, Fh=0.068 |
采用常数密度的边界元法可以求解潜体在分层流中定常运动引起的表面波和内波问题。在水深佛鲁德数比较小时,表面波和内波以横波为主,影响范围比较小;在接近内波模式的临界佛鲁德数 Fr2 时,表面波和内波中散波和横波的波形都比较明显,且内波的波高和波峰均接近最大值;在水深佛鲁德数比较大时,表面波和内波以散波为主。在同一航速、不同潜深的情况下,分布相似,但当潜体位于下层流体时,波峰与波谷的位置刚好与潜体位于上层流体时相反。
| [1] | KELLER J B, MUNK W H. Internal wave wakes of a body moving in a stratified fluid[J]. Physics of Fluids , 1970, 13 (6) :1425–1431. DOI:10.1063/1.1693096 |
| [2] | MILES J W. Internal waves generated by a horizontally moving source[J]. Geophysical Fluid Dynamics , 1971, 2 (1) :63–87. DOI:10.1080/03091927108236052 |
| [3] | HUGHES B A. The effect of internal waves on surface wind waves 2. Theoretical analysis[J]. Journal of Geophysical Research , 1978, 83 (C1) :455465. |
| [4] | TULIN M P, YAO Y T, WANG P. The generation and propagation of ship internal waves in a generally stratified ocean at high densimetric Froude number, including nonlinear effects[J]. Journal of Ship Research , 2000, 44 (3) :197–227. |
| [5] | RADKO T. Ship waves in a stratified fluid[J]. Journal of Ship Research , 2001, 45 (1) :1–12. |
| [6] | YEUNG R W, NGUYEN T C. Waves generated by a moving source in a two-layer ocean of finite depth[J]. Journal of Engineering Mathematics , 1999, 35 (1/2) :85–107. DOI:10.1023/A:1004399917692 |
| [7] | WEI G, LE J C, DAI S Q. Surface effects of internal wave generated by a moving source in a two-layer fluid of finite depth[J]. Applied Mathematics and Mechanics , 2003, 24 (9) :1025–1040. DOI:10.1007/BF02437635 |
| [8] |
朱伟, 尤云祥, 缪国平, 等. 两层流体中运动物体的兴波特性[J]. 船舶力学 , 2004, 8 (5) :1–9.
ZHU Wei, YOU Yun-xiang, MIAO Guo-ping, et al. Wave-making characteristics of a moving body in a two-layer fluid[J]. Journal of Ship Mechanics , 2004, 8 (5) :1–9. |
| [9] | BAL S, KINNAS S A, LEE H. Numerical analysis of 2-D and 3-D cavitating hydrofoils under a free surface[J]. Journal of Ship Research , 2001, 45 (1) :34–49. |
| [10] | HE G H. An iterative Rankine BEM for wave-making analysis of submerged and surface-piercing bodies in finite water depth[J]. Journal of Hydrodynamics , 2013, 25 (6) :839–847. DOI:10.1016/S1001-6058(13)60431-X |
| [11] | BELIBASSAKIS K A, GEROSTATHIS T P, KOSTAS K V, et al. A BEM-isogeometric method for the ship wave-resistance problem[J]. Ocean Engineering , 2013, 60 :53–67. DOI:10.1016/j.oceaneng.2012.12.030 |
| [12] | DOCTORS L J, BECK R F. Convergence properties of the Neumann-Kelvin problem for a submerged body[J]. Journal of Ship Research , 1987, 31 (4) :227–234. |
 2016, Vol. 38
2016, Vol. 38
