立管在涡激振动的作用下发生大变形,导致各立管间距变小,在立管遭受涡激振动疲劳损伤的同时大大提高了立管发生碰撞断裂的机率。在流场干涉效应下立管群的运动响应特性与独立立管有所区别[1~7],如即使未发生锁振立管也可能出现大振幅的驰振现象。而目前为止,学者们对于涡激振动抑制措施的研究基本都以单一结构物为设计对象[8~15],关于多根柔性圆柱体涡激振动抑制措施的研究依然很少[16]。因此,管群相互干涉下的涡激振动特点及抑制措施对管群之间相互作用的影响是今后研究工作的一个重要发展方向。本文采用商业软件 Ansys15.0 对均匀流下 2 根串联排列、轴间距为 5D 的相同深海立管模型在流场干涉效应下的涡激振动特性进行流固耦合研究,分析侧板对系统中不同位置处立管涡激振动的抑制效果。
1 数值计算方法 1.1 流体基本控制方程当外力在不考虑能量损耗的情况下,牛顿流体的运动可由质量守恒与动量守恒加以描述。
1)连续方程
连续方程是质量守恒定律在流体力学中的表现形式,对于不可压缩流体该方程可以表述为单位时间内流入该微元的净质量等于单位时间流出该微元的净质量。
| $\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial {{x}_{j}}}(\rho {{u}_{j}})=0$ | (1) |
2)动量方程
动量方程是动量守恒定律在流体力学中的表现形式,其本质是满足牛顿第二定律,该方程可以表述为对于一给定的流体微元,其具有的动量对时间的导数等于作用在该微元上的各种力之和。
| $\frac{\partial }{\partial t}(\rho ui)+\frac{\partial }{\partial xj}(\rho uiuj)=-\frac{\partial p}{\partial xi}+\frac{\partial }{\partial xj}(2\mu Sij)$ | (2) |
式中 xi,xj,ui,uj 分别为笛卡尔坐标系下的位置和速度分量;ρ,t,p 分别为密度、时间与压力;μ 为分子粘性;Sij 为应变率张量:
| ${{S}_{ij}}=\frac{1}{2}(\frac{\partial ui}{\partial xj}+\frac{\partial uj}{\partial xi})$ | (3) |
在流场作用下,顶张力柔性立管的结构运动微分方程为:
| $\begin{array}{*{35}{l}} \frac{{{\partial }^{2}}}{\partial {{z}^{2}}}\left( EI\frac{{{\partial }^{2}}v}{\partial {{z}^{2}}} \right)-\frac{\partial }{\partial z}\left( T\frac{\partial v}{\partial z} \right)+m\frac{{{\partial }^{2}}v}{\partial {{t}^{2}}}+c\frac{\partial v}{\partial t}={{F}_{(t)}}, \\ m\frac{{{\partial }^{2}}u}{\partial {{t}^{2}}}-EA\frac{{{\partial }^{2}}u}{\partial {{z}^{2}}}=0 \\ \end{array}$ | (4) |
式中,EI,EA,m 分别为抗弯刚度、抗拉刚度和单位长度的质量;T和F(t) 为张力和流体动力载荷;v和u 为横向位移和轴向位移。
对控制方程采用基于三维单元的有限元方法进行离散得到有限元方程:
| $M\ddot{d}+C\dot{d}+Kd={{F}_{(t)}}$ | (5) |
式中:d,
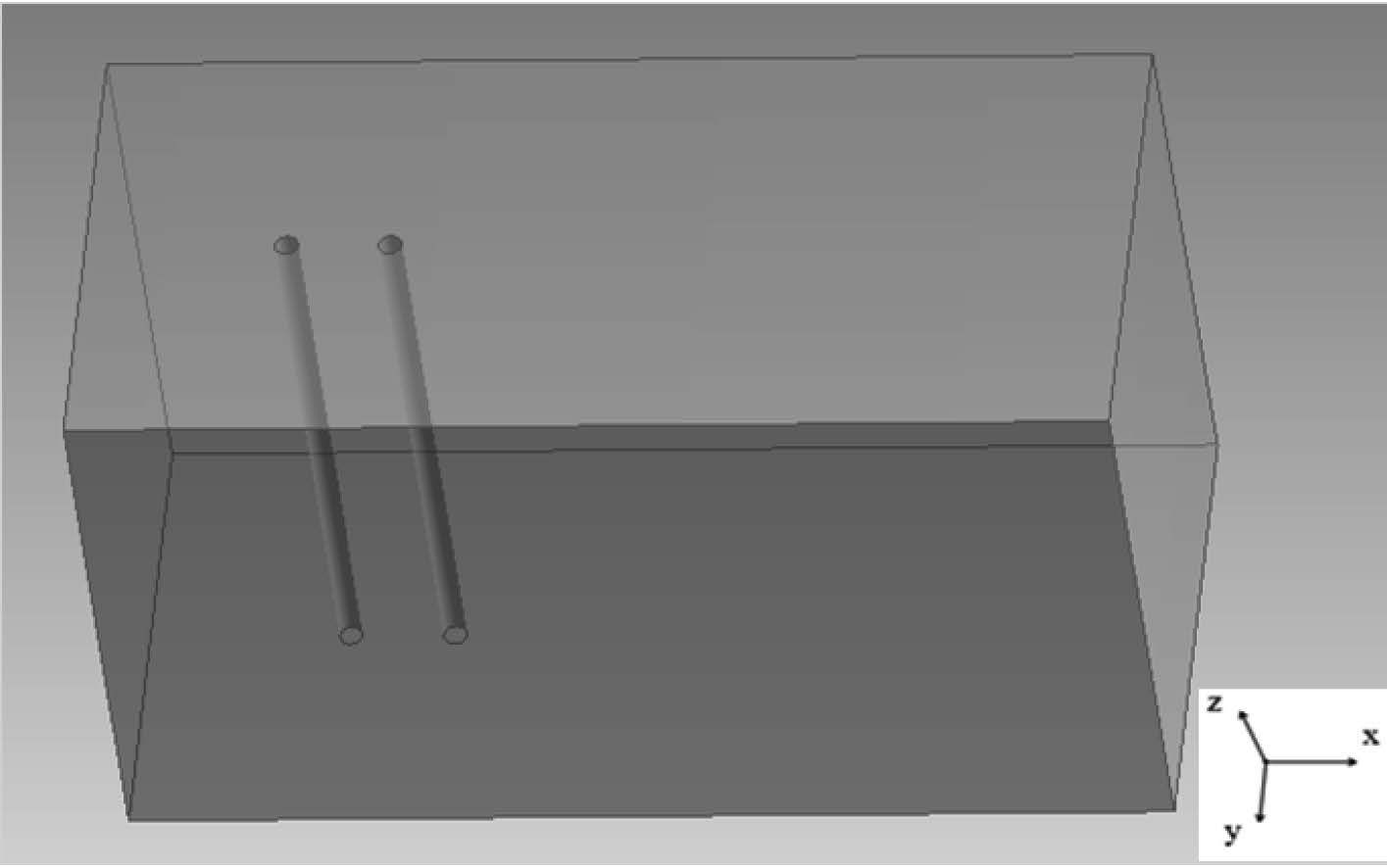
Tezduyar 和 Shih[17]提出,为避免选取矩形流域时下游壁面边界及侧壁面边界对圆柱周围流场产生影响,下游壁面边界距圆柱中心距离需大于 14.5 D,侧壁距圆柱中心需大于 8 D,三维圆管展向长度应大于 πD,其中 D 为圆柱直径。本文中选取计算流域如图 1 所示,上游立管中心距流域入口为 10 D,下游 30 D,距两侧壁面均为 10 D,展向长度取为立管长度。对于串列双立管,立管圆心间距取 5 D。入口条件为速度入口,U = 0.42 m/s,来流方向为 X 轴正向;出口条件为压力出口,忽略纵向速度梯度;上下壁面及圆柱表面满足无滑移固壁条件。柔性立管模型参考 Lehn(2003)模型试验[18],参数如表 1 所示。
|
图 1 计算模型及边界条件 Fig. 1 Model and boundary condition |
|
|
表 1 立管模型参数 Tab.1 Parameters of riser model |
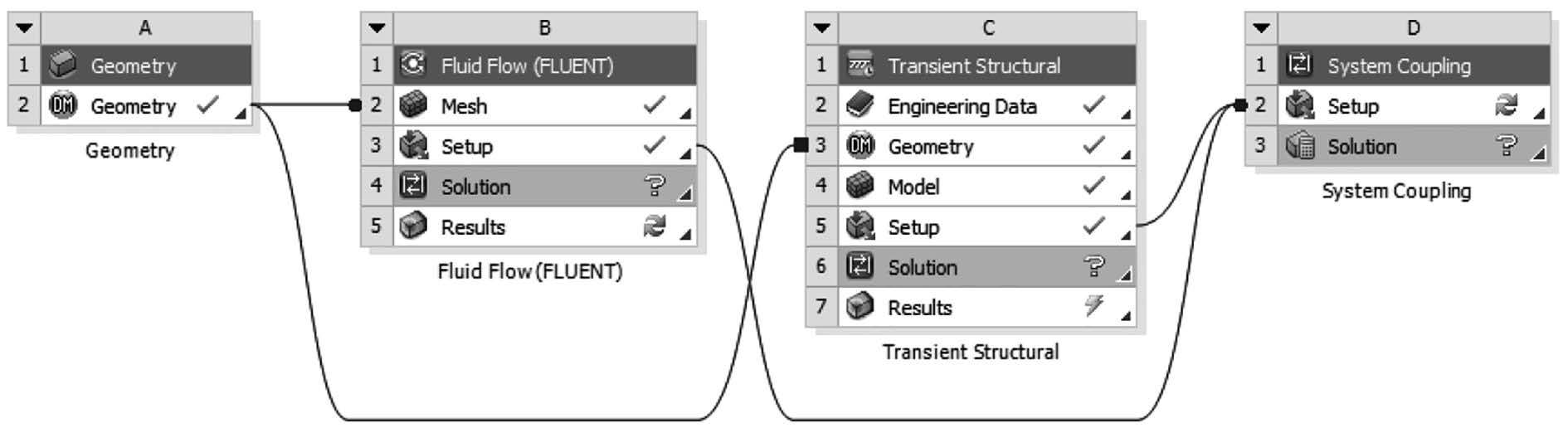
Ansys Workbench 平台流固耦合计算各模块连接如图 2 所示。首先利用 Design Modeler 模块建立流域及立管模型;其次在 Fluid Flow(Fluent)模块中划分流域网格并设置流场参数,网格划分如图 3 所示。流场采用标准 k-ω 模型,压力和速度耦合采用稳定性更高的 SIMPLEC 方法;压力项离散格式采用 2 阶精度,对动量方程的离散采用 2 阶迎风格式;由于动网格的使用时间离散方式只能采用 1 阶隐式;动网格技术采用网格光顺中的扩散光顺方法;计算中采用欠松弛技术以改善计算收敛条件,残差大小通常控制在 1.0E-05。然后在 Mechanical 模块中划分结构网格,见图 4,并将立管表面设为 Fluid Solid Interface,立管底部为简支端,上部顶张力为 817 N 且沿轴向立管可自由运动,XY 方向固定。最后利用 System Coupling 模块进行流固耦合及数据传递,3 个模块中的时间步长及计算总时长必须保持一致。
|
图 2 Ansys 处理流固耦合问题时各模块之间的连接 Fig. 2 The connection of different parts of Ansys in solution of FSI |

|
图 3 流域网格划分 Fig. 3 Mesh generation of fluid field |

|
图 4 立管网格划分 Fig. 4 Mesh generation of riser |
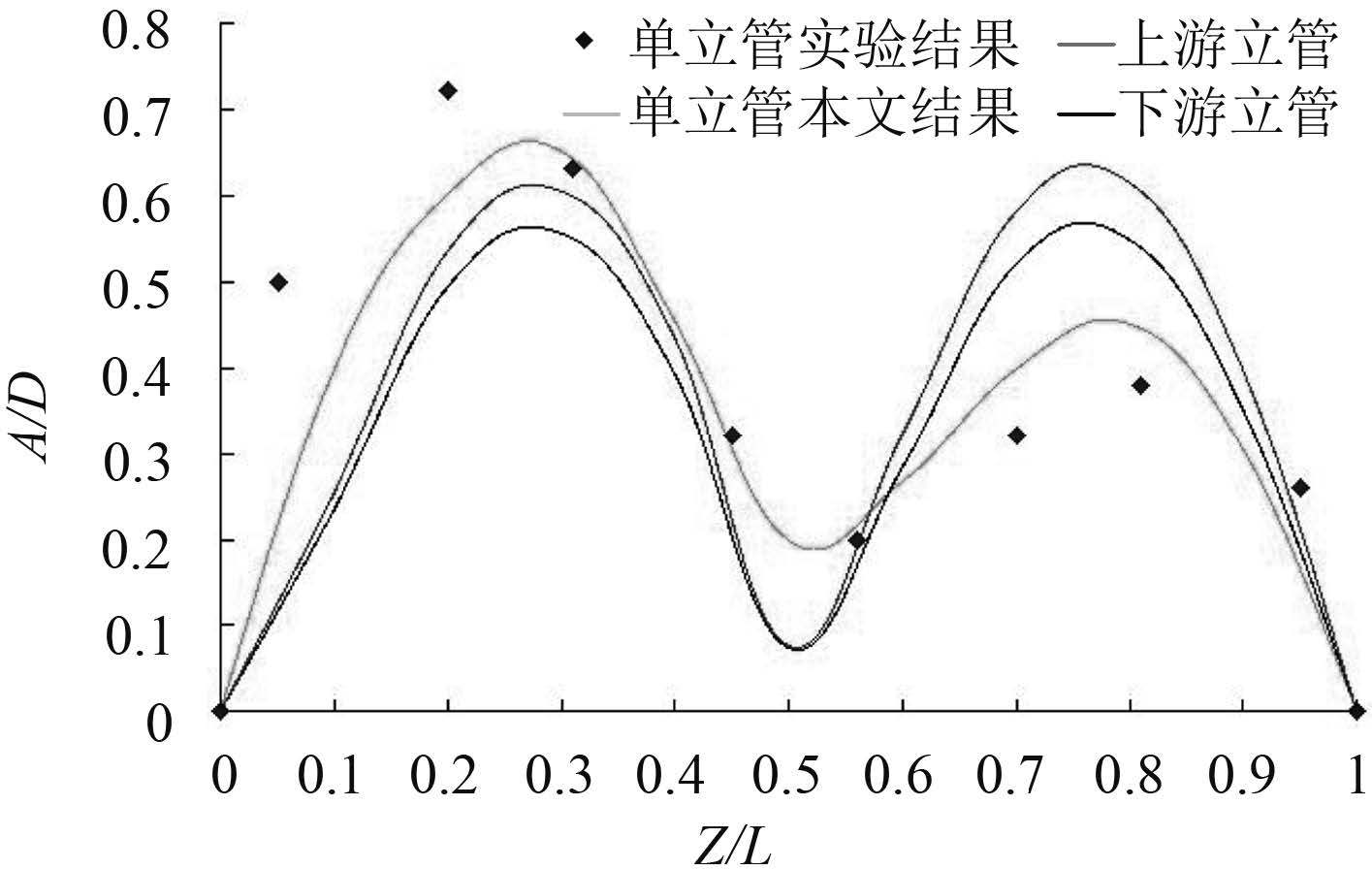
图 5 为立管横向无量纲振幅均方根曲线。首先,由本文光滑单立管的数值结果与文献[18]实验结果对比,2 组数据立管中下部模拟较好,在 Z/L = 0~0.3 及 0.9~1 范围内数值结果较实验值偏小,中上部偏大,由于试验与数值模拟的差别以及数值计算中网格划分方式、参数设置不同等原因,导致一定的误差,但误差尚可以接受;且 2 组数据都反映了立管在此来流情况下能够发生 2 阶振动,下部变形大于上部,很好地验证了本文流固耦合数值模拟的可行性。对于串列双立管,上半部分变形较单立管有所增加,下半部分有所减小;下游立管无因次均方根振幅略大于上游立管。崔洋洋[19]对相同立管模型、间距为 4D 的光滑双立管进行数值计算,与单立管对比得到了相似的结论。
|
图 5 立管横向无量纲振幅均方根 Fig. 5 Dimensionless amplitude RMS in CF of risers |
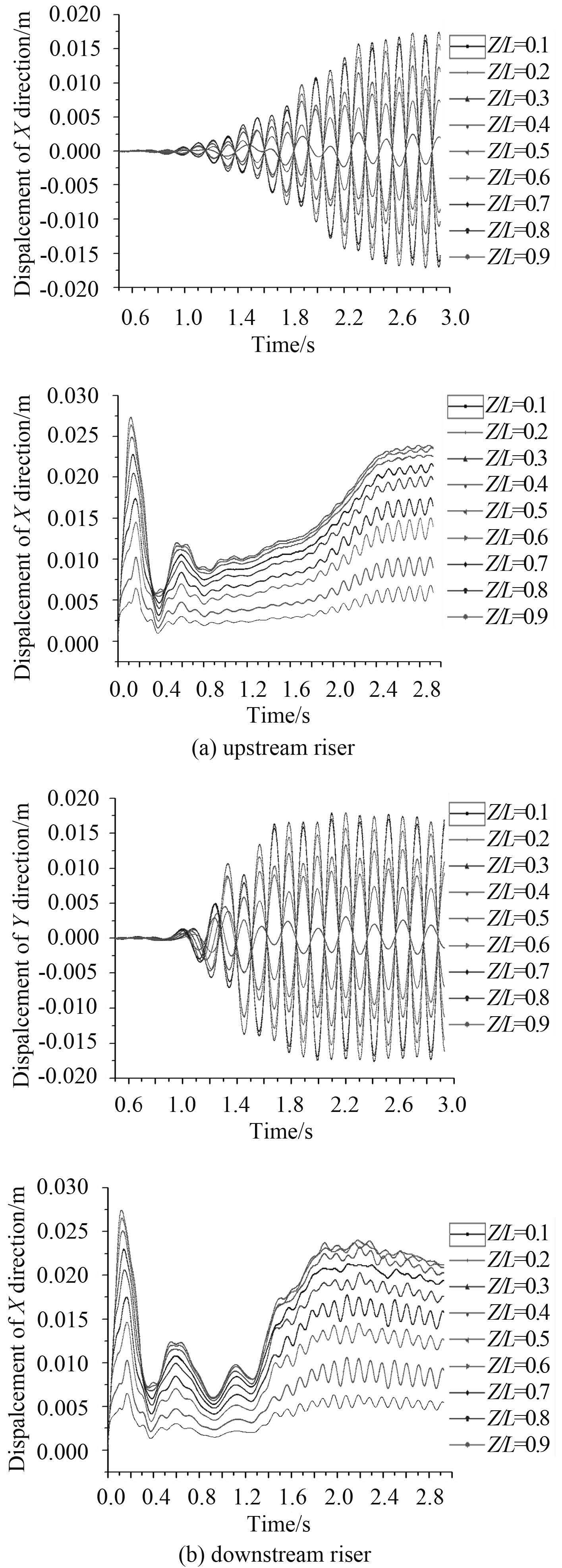
图 6 和图 7 分别为光滑双立管和附加侧板双立管横向(Cross Flow,CF)及顺向(In Line,IL)位移时间图。对于光滑立管,下游立管在上游立管的尾流作用下产生振动,并且比上游立管更快达到稳定振动状态;在横流向,同一时刻对应立管不同位置处的振动幅值有正有负,且正值与负值各自对应点关于 Z = 0.5 L 对称,说明立管最终锁定在二阶振动模态,此外,对于不同立管,同一节点振动方向相反,说明上下游立管在横向为反相振动;在顺流向,同一极值时刻对应各点的幅值均为最大值或最小值,说明在顺流向上下游立管均为 1 阶振动模态,且为同相振动。对于附加侧板的双立管,在横流向,同一极值时刻,同一立管各点对应幅值均为最大值或最小值,说明了双立管在横流向为 1 阶振动,同样两立管为反相振动,最大振幅点在 Z/L = 0.5 节点处;在顺流向,由图可以看出,上游立管在来流作用下发生了大变形,到达平衡位置后做缓慢振动,其振幅几乎为 0;下游立管在尾流作用下同样发生了大变形,然后在平衡位置振动,其振幅大于上游立管。
|
图 6 光滑双立管横向及顺向位移-时间图 Fig. 6 Displacement-time diagram in CF and IL of double smoothed risers |
|
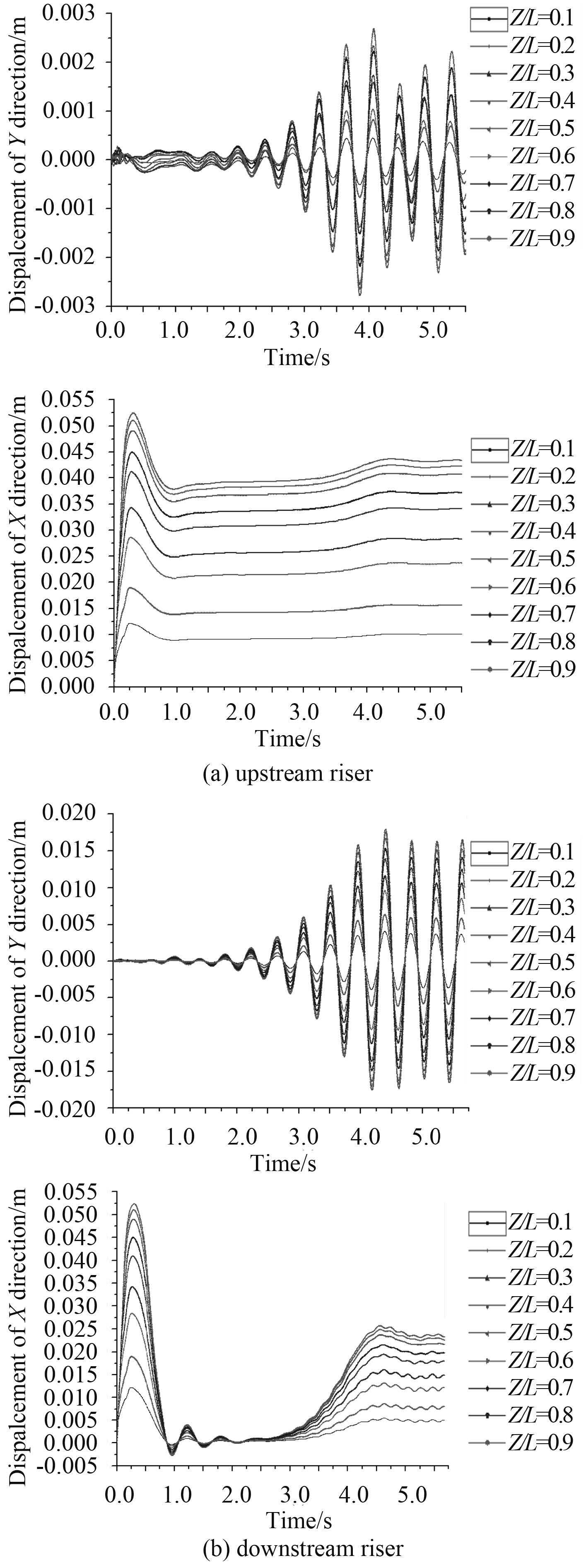
图 7 附加螺旋侧板立管横向及顺向位移-时间图 Fig. 7 Displacement-time diagram in CF and IL of risers with helical strakes |
对各振动曲线进行傅里叶变换求得其振动主频,并和横向变形最大值、顺向位移最大值列于表 2,通过与同等条件下的单根柔性立管进行对比,分析 2 种情况下立管振动特性的不同。结果发现:对于光滑双立管,上游立管和下游立管的振动频率一致,说明在尾流干涉作用下双立管达到了同步振动,且顺向振动频率与横向振动约满足 2 倍关系;此外,顺向位移超过了横向最大变形,说明了柔性立管由于弯曲强度削弱导致顺流向更容易发生大变形。附加侧板后,双立管横向振动频率均由原来的 4.808 Hz 降至 2.345 Hz,使振动约减缓了 1 倍;上游立管在侧板的作用下横向振幅降幅显著,振幅最大值由 0.87 D 减小至 0.1 D;下游立管振幅反而略有增加,值为 0.89 D;由于侧板的存在,阻力增大,使上游立管顺向最大位移值约增大 1 倍,下游立管的顺向位移响应增幅很小。
|
|
表 2 振动特性分析 Tab.2 Vibration characteristic analysis |
图 8 和图 9 分别为光滑双立管和附加侧板立管横向振型图。光滑双立管在横流向为反相振动,锁定在 2 阶模态。附加侧板后锁定在 1 阶振动模态,且上游立管在横流向做微幅振荡,下游立管做大幅振动。
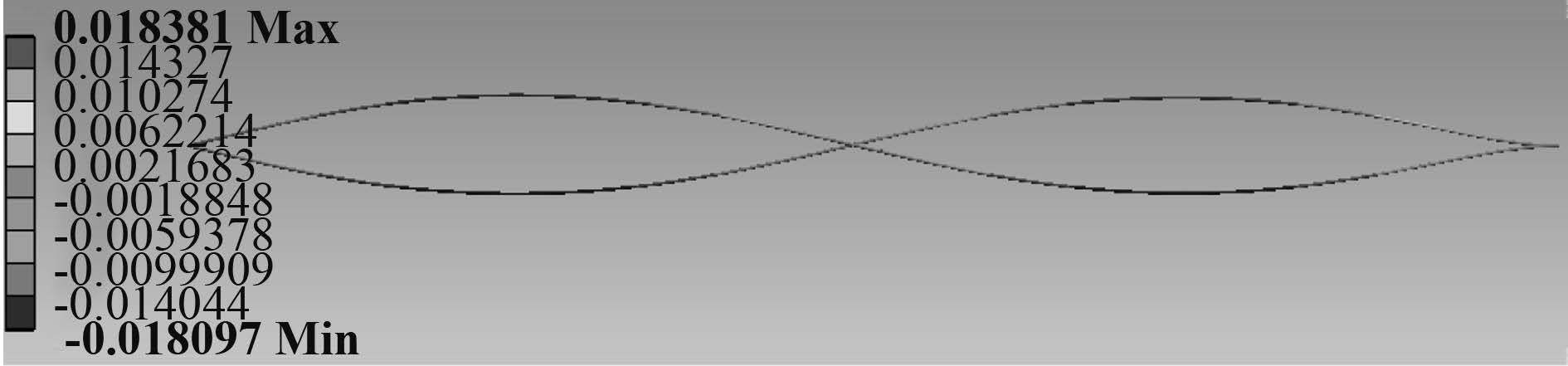
|
图 8 光滑双立管横向振型图 Fig. 8 Vibration mode of smoothed double risers in CF |
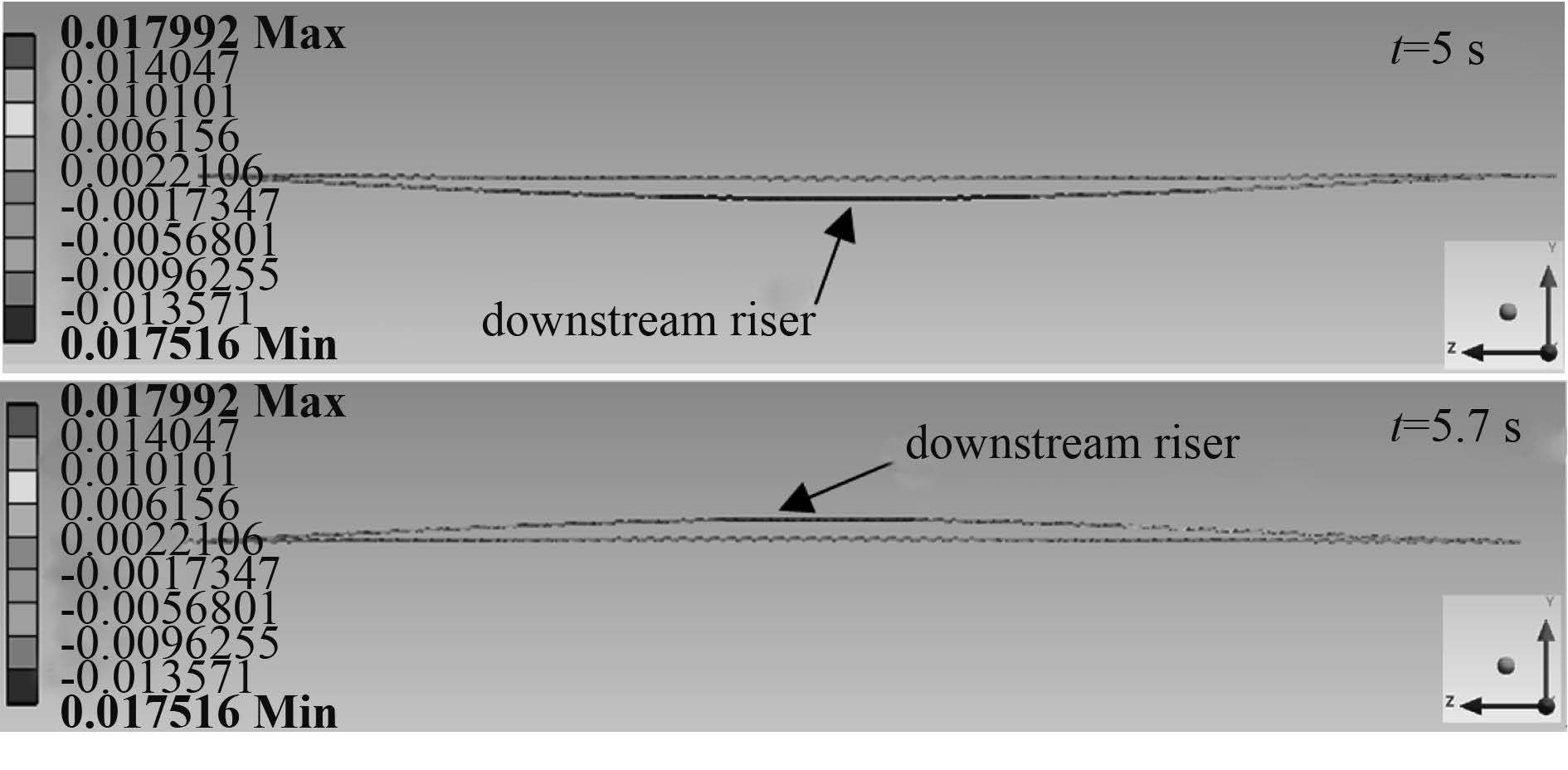
|
图 9 附加螺旋侧板双立管横向振型图 Fig. 9 Vibration mode in CF of double risers with helical strakes |
图 10 为光滑双立管和附加侧板立管顺向振型图。2 种工况下,立管在顺流向均为一阶振动,且上游立管顺向位移略大于下游立管,光滑双立管在运动过程中最小间距为 4.88 D,略低于静止时刻立管间距,附加侧板后,由于上游立管顺向位移变大,导致双立管间距进一步减小,约为 3.95 D,说明侧板的存在虽然降低了立管双向振动频率及上游立管横向振动幅值,但增加了立管顺流向碰撞的机率。图 11 为立管总变形图。
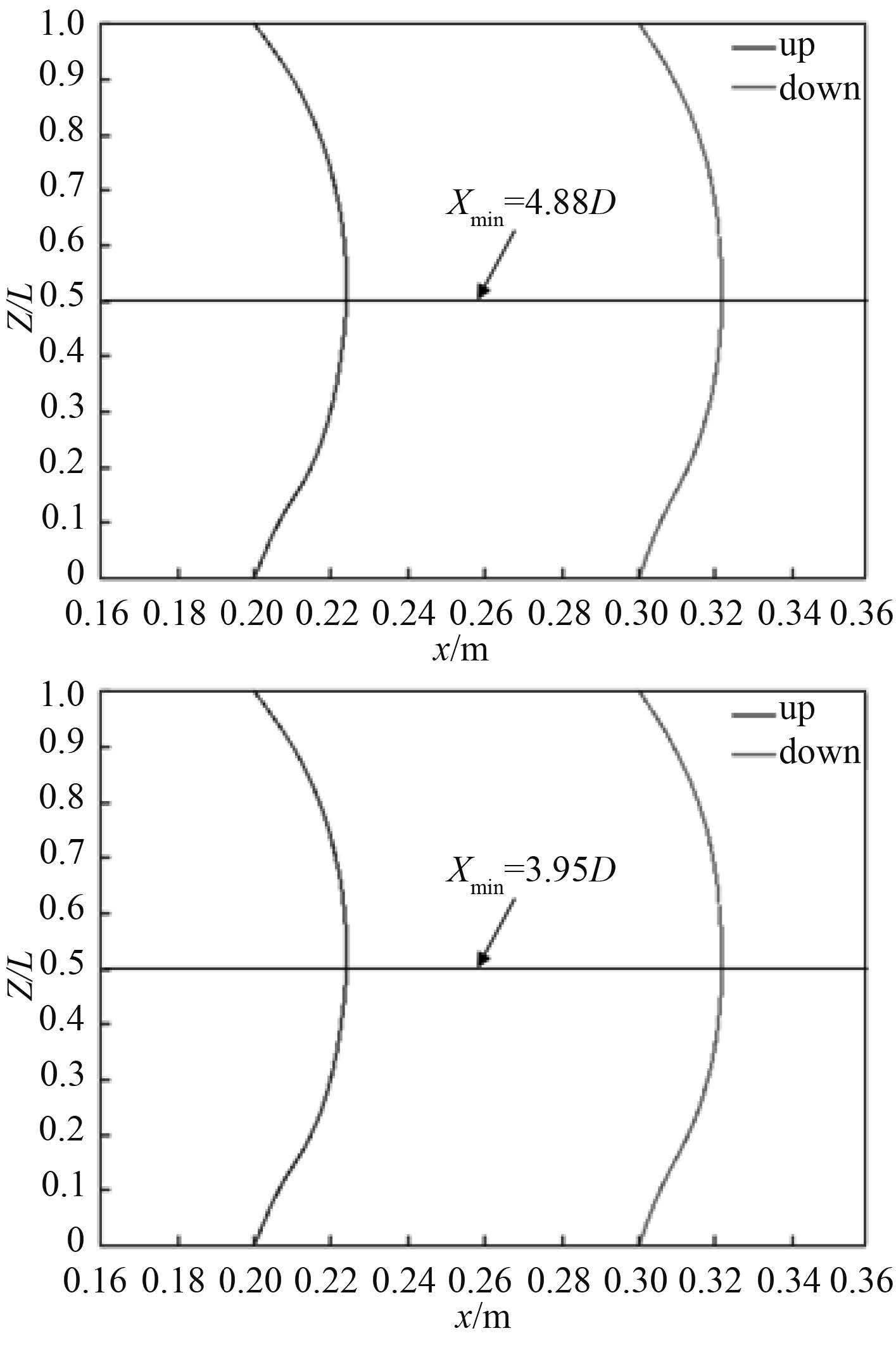
|
图 10 光滑双立管及附加螺旋侧板立管顺向振型图 Fig. 10 Vibration mode in IL of smoothed double risers and risers with helical strakes |

|
图 11 光滑双立管及附加螺旋侧板立管总变形图 Fig. 11 Total deformation of smoothed double risers and risers with helical strakes |
对于光滑双立管,由涡量图 12 可以看出,当立管间距为 5 D 时,两立管之间有完整的旋涡脱落。在 Z/L = 0.1,0.3 和 Z/L = 0.5,0.7 截面处,双立管上下部分旋涡脱落方向相反,导致立管振动方向相反,立管间涡泄为 P + S 模式,下游立管后缘处为 2S 模式,且为双排涡,Z/L = 0.3 和 0.7 两个截面处旋涡横向间距较其他截面偏大,约为一倍立管直径的距离,与立管横向最大变形位置相对应。Z/L = 0.5 截面处两立管间旋涡为单排涡,下游立管尾流场由于立管中间位置变形较小呈现 2 条横向间距很小、几乎平行的尾涡。且由 Z/L = 0.3 和 Z/L = 0.7 截面图可以清晰地看出,下游立管近壁面处的尾涡脱落方向恰好与上游立管尾缘处旋涡脱落方向相反,说明同一高度处上下游立管横向振动方向相反。附加螺旋侧板后,两立管之间的流动情况较为杂乱,来流绕过上游立管壁面从侧板上分离。但下游立管在上游立管的尾流作用下其尾流场依然有相当量的旋涡脱落,导致下游立管发生了大振幅振动,对于不同截面,下游立管均偏向中心线的一侧,说明立管横流向振动为一阶模态。由附加螺旋侧板的立管三维涡量图 13 可以看出,下游立管的尾涡在轴向上呈螺旋状脱落。另外,通过不同截面处尾涡的差异及三维涡量图直观地表现了高速来流下立管尾流场旋涡发放的三维特性。

|
图 12 光滑立管及附加侧板立管的涡量切片图 Fig. 12 Vorticity slice graph of smoothed riser and risers with helical strakes |

|
图 13 光滑立管及附加螺旋侧板立管三维涡量图 Fig. 13 3D vorticity of smoothed riser and riser with helical strakes |
本文对 Re = 7 800 的均匀来流下长径比为 482 的串列双立管进行了数值模拟,研究其涡激振动特性及侧板对双立管涡激振动的抑制效果,主要结论如下:
1)当立管间距为 5 D 时,光滑双立管之间有完整的尾涡脱落,出现了多种脱落模式。上下游立管达到了同步振动,且顺向振动频率与横向振动均满足约 2 倍的关系;下游立管横向变形略大于上游立管;但顺向位移上游立管略大于下游立管,使立管顺向间距有所减小。
2)附加侧板后双立管振动频率约减缓了一倍,横向振动模态亦有所降低,上游立管横向抑制效果更为明显,下游立管两向位移响应变化不大,但由于上游立管顺向变形进一步增大导致立管最小间距较光滑立管有所减小,增大了碰撞机率。这说明对抑制措施在立管群中的应用需要做更加深入的研究,寻求合理的方式以提高抑制措施对各立管的抑制效率,或者寻求更加高效适用的方法削弱立管涡激振动损伤,提高立管安全使用寿命。
| [1] | HUANG K, CHEN H C, CHEN C R. Vertical riser VIV simulation in sheared current[J]. International Journal of Offshore and Polar Engineering , 2012, 22 (2) :142–149. |
| [2] |
吴学敏. 考虑大变形的深水立管涡激振动非线性分析方法研究[D]. 青岛: 中国海洋大学, 2013.
WU Xue-min. Study on non-linear analysis method on VIV of deepwater risers with large deflection[D]. Qingdao: Ocean University of China, 2013. http://cdmd.cnki.com.cn/article/cdmd-10423-1013348310.htm |
| [3] |
韩翔希. 柔性立管流固耦合特性数值模拟研究[D]. 广州: 华南理工大学, 2014.
HAN Xiang-xi. Investigation on numerical simulation of the fluid-solid interaction characteristics for flexible riser[D]. Guangzhou: South China University of Technology, 2014. http://cdmd.cnki.com.cn/article/cdmd-10561-1014063800.htm |
| [4] |
郭海燕, 牛建杰, 李效民, 等. 海洋立管涡激振动模型的实验验证[J]. 中国海洋大学学报 , 2015, 45 (6) :108–115.
GUO Hai-yan, NIU Jian-jie, LI Xiao-min, et al. Comparisons of numerical simulation and experimental study on vortex-induced vibration of marine riser under stepped current[J]. Periodical of Ocean University of China , 2015, 45 (6) :108–115. |
| [5] |
姚熊亮, 陈起富. 串列双圆柱在均匀流场中涡激振动综述[J]. 哈尔滨船舶工程学院学报 , 1994, 15 (4) :1–16.
YAO Xiong-liang, CHEN Qi-fu. Review of vortex-induced vibrations of two circular cylinders in tandem arrangement[J]. Journal of Harbin Shipbuilding Engineering Institute , 1994, 15 (4) :1–16. |
| [6] |
魏东泽. 基于雷诺相似的串列双立管涡激振动研究[D]. 青岛: 中国海洋大学, 2012.
WEI Dong-ze. Study on vortex-induced vibration of two tandem risers based on Reynolds similarity criterion[D]. Qingdao: Ocean University of China, 2012. http://epub.cnki.net/kns/detail/detail.aspx?QueryID=79&CurRec=1&recid=&FileName=1012506039.nh&DbName=CMFD201301&DbCode=CMFD&pr= |
| [7] |
娄敏, 轩红超. 尾流干涉下考虑流固耦合作用的海洋立管涡激振动的数值模拟[J]. 船海工程 , 2015, 44 (2) :141–145.
LOU Min, XUAN Hong-chao. Numerical simulation of fluid-structural interaction for vortex-induced vibration of risers with effects of wake interference[J]. Ship & Ocean Engineering , 2015, 44 (2) :141–145. |
| [8] |
张友林. 海洋立管涡激振动抑制方法研究[D]. 镇江: 江苏科技大学, 2011.
ZHANG You-lin. Study method of vortex-induced vibration suppression of marine riser[D]. Zhenjiang: Jiangsu University of Science and Technology, 2011. http://cdmd.cnki.com.cn/article/cdmd-10289-1011289556.htm |
| [9] |
韩韶英. 带轴向板条圆柱绕流数值模拟研究[D]. 青岛: 中国海洋大学, 2011: 47-52.
HAN Shao-ying. Numerical study of flow around a circular cylinder with longitudinal slats[D]. Qingdao: Ocean University of China, 2011: 47-52. http://epub.cnki.net/kns/detail/detail.aspx?QueryID=83&CurRec=1&recid=&FileName=1011229571.nh&DbName=CMFD2012&DbCode=CMFD&pr= |
| [10] |
吴浩. 多根控制杆对细长柔性立管涡激振动抑制作用的实验及数值研究[D]. 大连: 大连理工大学, 2013.
WU Hao. Experimental and numerical studies on the suppression of vortex induced vibration of long flexible riser by multiple control rods[D]. Dalian: Dalian University of Technology, 2013. http://epub.cnki.net/kns/detail/detail.aspx?QueryID=87&CurRec=1&recid=&FileName=1014154761.nh&DbName=CDFD1214&DbCode=CDFD&pr= |
| [11] |
郑婷婷. 螺旋侧板抑制海洋立管涡激振动的机理研究[D]. 镇江: 江苏科技大学, 2013.
ZHENG Ting-ting. Mechanism research of VIV suppression by the use of helical strake for marine riser[D]. Zhenjiang: Jiangsu University of Science and Technology, 2013. http://cdmd.cnki.com.cn/article/cdmd-10289-1014034752.htm |
| [12] |
矫滨田. 立管涡激振动抑制装置海上试验[J]. 管道技术与设备 , 2013 (3) :1–3.
JIAO Bin-tian. An offshore test on VIV suppression device of riser[J]. Pipeline Technique and Equipment , 2013 (3) :1–3. |
| [13] |
朱仁庆, 郑婷婷, 李紫晖. 带分隔板的海洋立管尾流场数值研究[J]. 船舶力学 , 2014, 18 (7) :746–753.
ZHU Ren-qing, ZHENG Ting-ting, LI Zi-hui. Numerical simulation on the wake field of marine riser fitted with a splitter plate[J]. Journal of Ship Mechanics , 2014, 18 (7) :746–753. |
| [14] | QUEN L K, ABU A, KATO N, et al. Investigation on the effectiveness of helical strakes in suppressing VIV of flexible riser[J]. Applied Ocean Research , 2014, 44 :82–91. DOI:10.1016/j.apor.2013.11.006 |
| [15] |
高云, 付世晓, 宋磊建. 柔性立管涡激振动抑制装置试验研究[J]. 振动与冲击 , 2014, 33 (14) :77–83.
GAO Yun, FU Shi-xiao, SONG Lei-jian. Experimental investigation on the suppression device of VIV of a flexible riser[J]. Journal of Vibration and Shock , 2014, 33 (14) :77–83. |
| [16] |
关德宝, 黄维平, 宋虹. 串列圆柱体尾流、尾涡耦合振动试验研究[J]. 振动与冲击 , 2014, 33 (22) :26–29.
GUAN De-bao, HUANG Wei-ping, SONG Hong. Experimental investigation of wake flow and wave-vortex coupled vibration of two tandem and cylinders[J]. Journal of Vibration and Shock , 2014, 33 (22) :26–29. |
| [17] | TEZDUYAR T E, SHIH R. Numerical experiments on downstream boundary of flow past cylinder[J]. Journal of Engineering Mechanics , 1991, 117 (4) :854–871. DOI:10.1061/(ASCE)0733-9399(1991)117:4(854) |
| [18] | LEHN E. VIV suppression tests on high L/D flexible cylinders (main reports)[R]. USA: ExxonMobil Upstream Research Company, 2003. |
| [19] |
崔洋洋. 串列布设立管干涉问题流固耦合研究[D]. 大连: 大连理工大学, 2013.
CUI Yang-yang. Fluid-structure interaction research of interference of tandem arranged risers[D]. Dalian: Dalian University of Technology, 2013. http://cdmd.cnki.com.cn/article/cdmd-10141-1013200407.htm |
 2016, Vol. 38
2016, Vol. 38
