泡沫夹层结构具有轻质、高比强度、高比刚度、抗振、隔热等优良特性,在航空航天、汽车、轨道交通以及船舶领域的应用日渐广泛[1]。这种结构的芯层材料是一种多孔材料,在爆炸/冲击载荷下发生压溃变形,吸收爆炸冲击能量,并能有效地衰减冲击波[2, 3]。研究结果表明,夹芯板的面板及芯层高度配置直接影响其抗爆性能[4],因此探究其结构参数对其抗爆性能的影响规律成为了近年来的研究焦点。
本文基于 Abaqus 有限元分析软件[5],从夹芯板的损伤及吸能角度,分析结构参数及载荷参数对其抗爆性能的影响。
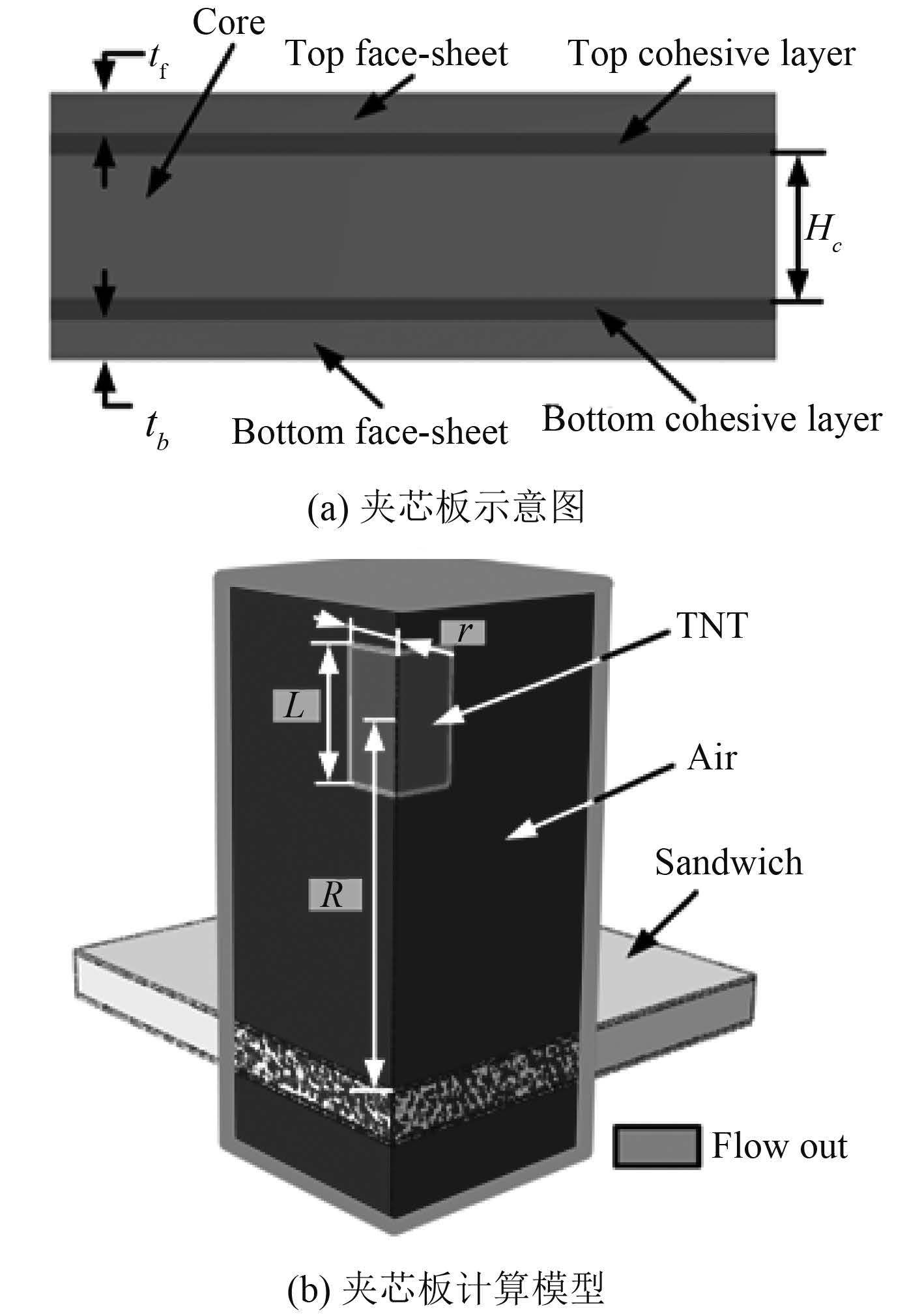
1 计算模型和仿真方法 1.1 计算模型研究的夹芯板结构是由 5 部分组件构成,分别是上面板、下面板、芯层、上粘接层及下粘接层,截面示意图如图 1(a)所示,其有效承载范围大小为 300 mm × 288 mm。同时,为分析炸药当量、夹芯板芯层配置及上面板厚度配置对其抗爆性能的影响,设置了表 1 所列工况。夹芯板结构参数见表 1,计算过程中,夹芯板边界均为四周刚固。所有工况中,所用炸药均为圆柱形 TNT,装药位置位于夹芯板中心点正上方,并保持爆距(即炸药中心点距夹芯板上表面的距离)R = 100 mm 不变。考虑到炸药及夹芯板结构的对称性,为减少计算规模,进行计算时只建立 1/4 模型,并在对称面上施加对称边界条件。另外,鉴于当前问题的爆炸载荷呈现出较强的局部性,夹芯板附近的空气域可以只建立中心部分[6],其尺寸为 70 mm × 70 mm × 170 mm,并在空气域外部设置无反射边界条件,整个计算模型如图 1(b)所示。
|
图 1 夹芯板示意图和夹芯板计算模型 Fig. 1 Schematic illustration of sandwich panel and view of finite element model. |
|
|
表 1 计算工况 Tab.1 Computation conditions |
为了更好地反映结构在爆炸载荷作用下的变形及损伤情况,夹芯板面板及芯层均采用实体单元建立(C3D8R),粘接介质采用粘接单元建立(COH3D8),空气域和炸药采用三维多物质欧拉单元建立(EC3D8R)。面板在平面内单元尺寸为 1 mm,沿板厚方向划分 4 层单元;芯层在平面内单元尺寸为 1 mm,沿高度方向单元尺寸为 1.5 mm;粘接介质厚度为 0.01 mm,在平面内单元尺寸为 1 mm,沿板厚方向划分 1 层单元。粘接层与面板,以及粘接层与芯层之间采用共节点处理。空气域采用 1 mm 的大小进行均匀网格划分,并采用关键字 *CONTACT 定义夹芯板上面板与空气及爆炸产物的耦合关系。
1.2 材料模型及材料参数夹芯板面板材料为 304 不锈钢,其弹性模量为 200 GPa,密度为 7 900 kg/m3。采用 Johnson-Cook 材料模型(*Plastic,hardening = JOHNSON COOK,*Rate Dependent,type = JOHNSON COOK)描述该材料在冲击载荷作用下的动态屈服应力 σy,具体材料参数见文献[7]。
芯层选用 Divinycell 系列 H250 型号的 PVC 泡沫,其密度为 250 kg/m3,弹性模量为 170 MPa[8],弹性泊松比为 0.3,塑性泊松比为 0。并使用可压碎泡沫模型[9]来描述泡沫的力学性能,其中材料应变强化效应可以通过屈服面表示为:
| $F=\sqrt{{{q}^{2}}+{{\beta }^{2}}\left( p-{{p}_{0}} \right)}-B=0\text{,}$ | (1) |
式中:p 为静水压力;q 为等效 Mises 应力;β 为该椭圆的横、纵向长度比,称为形状因子。同时该形状因子也可以表示为:
| $\beta =\frac{3k}{\sqrt{\left( 3{{k}_{t}}+k \right)\left( 3-k \right)}}。$ | (2) |
式中:
粘接材料为线弹性正交材料,并通过拉伸破坏准则[12]给定材料的损伤模型。由于材料的失效应力没有对应的实验参数,因此在仿真过程中调整失效应力值直至结构失效过后的面板与芯层的空穴面积与实验得到的空穴面积接近,从而反演得到粘接层失效时对应的最大法向拉伸应力和平面剪切应力。具体粘接材料属性见表 2,同时为了增加计算过程中的稳定增量步长,粘接材料密度取为 9 600 kg/m3[12]。
|
|
表 2 粘接层的力学性能参数 Tab.2 Material and damage parameters for cohesive layers |
TNT 炸药采用 JWL 状态方程描述(*Eos,type = JWL),具体参数见文献[13]。空气采用理想气体状态方程描述(*Eos,type = IDEALGAS),具体参数见文献[14]。
1.3 模型验证采用文献[15]中公布的实验结果(工况 SS-1~SS-3)作为前述数值计算方法的验证。图 2 给出了爆炸冲击载荷作用下 PVC 泡沫夹芯板实验与数值计算的半剖面变形模式。从图中可以看出,仿真计算得到的夹芯板变形及失效模式与实验结果具有较好的一致性,均表现为上面板局部弯曲变形,下面板整体弯曲变形,泡沫芯层在中心区域发生压溃变形,面板-芯层粘接界出现完全失效并导致面板与芯层之间出现空穴。但是仿真所使用的材料模型中未考虑 PVC 材料的剪切破坏,因此未能反映出实验中 PVC 泡沫芯层出现的剪切破坏。

|
图 2 实验及仿真结果夹芯板变形模式 Fig. 2 Comparison between the experimental results and numerical results |
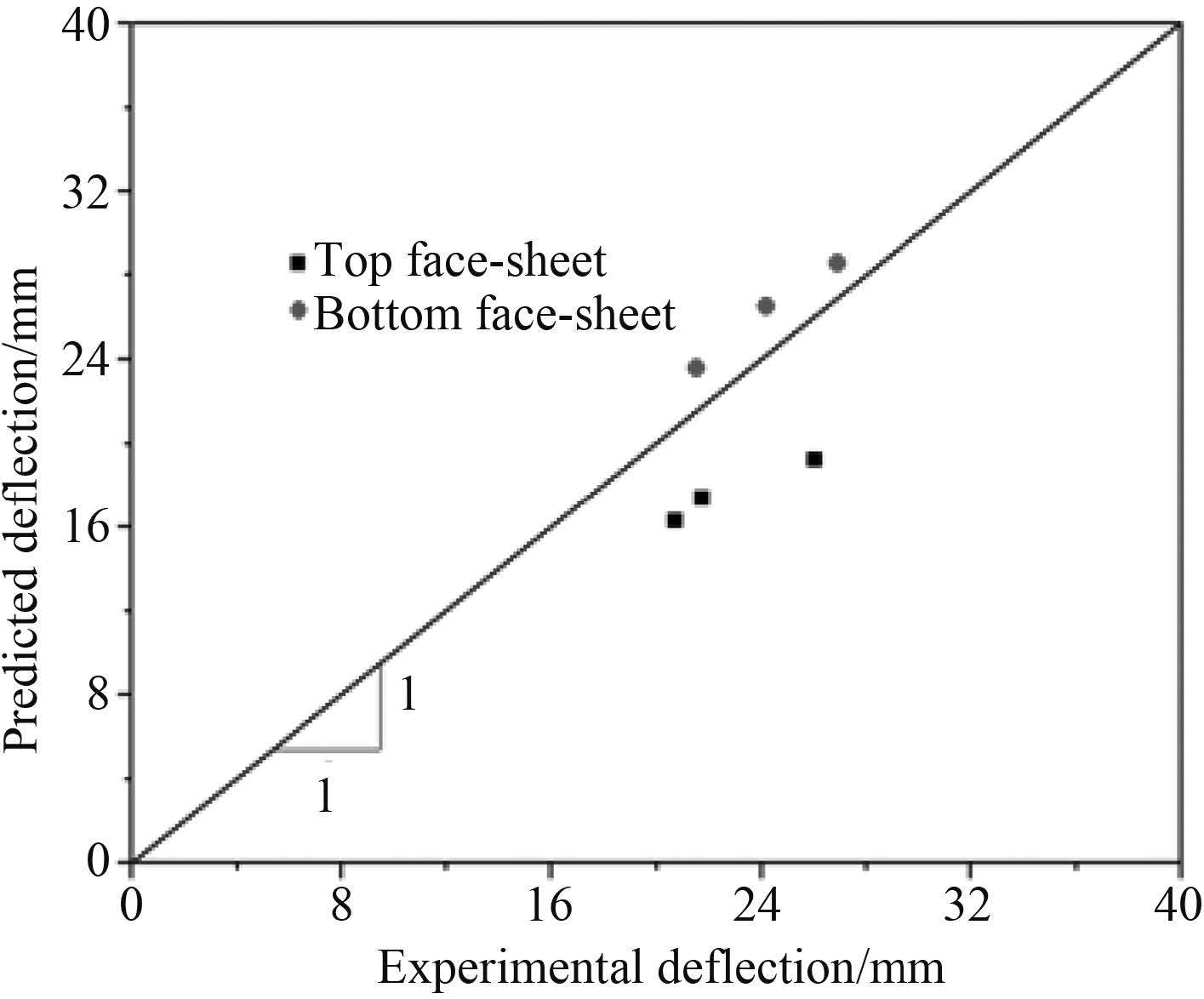
表 3 和图 3 给出了实验测量及数值计算得到的试件面板中心点最终变形值和对比图。整体上,数值计算的下面板中心点最终变形与实验吻合较好,而上面板残余变形相对偏小,这是由于仿真未考虑芯层的破坏,这导致了仿真过程中芯层强度比实际芯层强度偏大,从而对上面板的变形具有一定的抑制作用。
|
|
表 3 仿真与实验结果中心点变形对比 Tab.3 Comparison of measured and predicted sandwich panel midpoint deflection |
|
图 3 仿真与实验结果中心点变形对比 Fig. 3 Numerical versus experimental midpoint deflections. |
本节选取工况 SS-2 计算结果,以说明 PVC 泡沫夹芯板在爆炸载荷作用下的响应过程。图 4 给出了夹芯板在爆炸载荷作用下不同时刻的变形云图。在 t = 0 μs 时,炸药起爆,生成高压气团,并由此产生爆炸冲击波;在 t = 20 μs 时,爆炸冲击波作用在夹芯板的上面板处,使上面板获得初始动能。之后,上面板运动,并压缩芯层,此时,结构下面板保持不动,此时结构的变形主要表现为上面板局部弯曲及芯层局部压缩。在 t = 58 μs 时,芯层压缩量达到最大值,芯层失去缓冲作用,之后,载荷通过芯层传递到下面板,从而使下面板开始运动。并且,在 t = 80 μs 时,上面板与芯层脱离,在此阶段内,结构的变形主要表现为结构整体弯曲及拉伸变形。

|
图 4 SS-2 试件在爆炸载荷作用下的响应过程 Fig. 4 The response process of SS-2 |
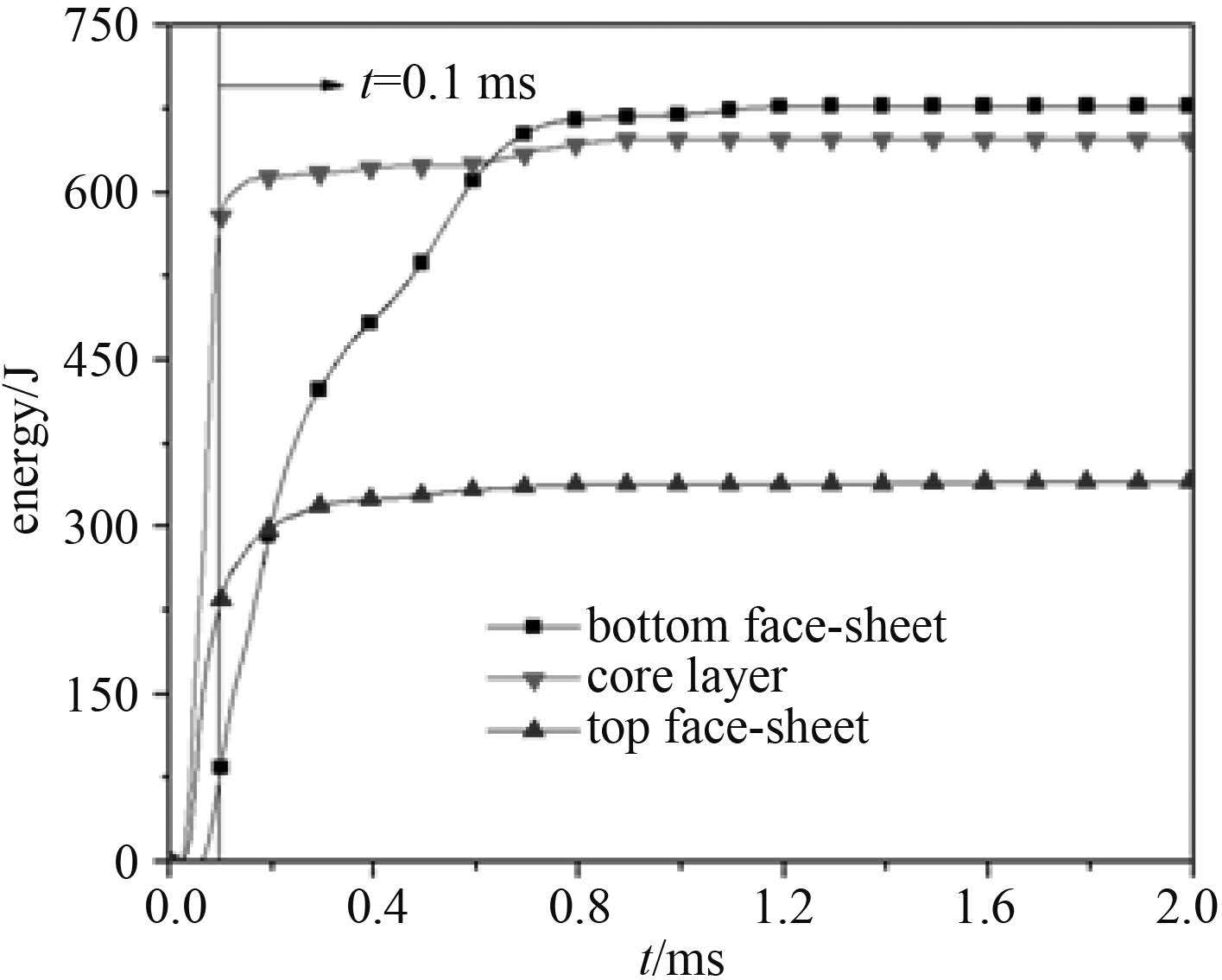
泡沫夹芯板在爆炸载荷作用下,由于芯层材料的可压缩性,结构具有较好的能量吸收性能。爆炸冲击波作用在夹芯板上的过程中,结构的动能转换为夹芯板的内能,并通过材料的塑性变形及破坏耗散能量。对于本文研究对象,粘接材料产生破坏所耗散的能量其相对较小,以工况 SS-2 为例,其粘接介质几乎完全损坏,所耗散的能量大小为整体结构耗散能量的 0.6‰,因此本文不予讨论。本研究主要通过面板及芯层的塑性应力能来表征其能量吸收特性。图 5 给出了 SS-2 夹芯板上面板、下面板及芯层的能量吸收时程曲线。结合图 4 和图 5 可看出,在 0.1 ms 之前,上面板运动使得芯层压缩,结构主要通过芯层压缩变形进行能量耗散;之后,由于粘接层的破坏,背面板与芯层脱离,背面板发生整体弯曲及拉伸变形,其所吸收的能量迅速增加,此阶段主要通过面板的变形吸收能量。
|
图 5 SS-2 试件组成部件能量吸收时程曲线 Fig. 5 Energy absorption time histories of each component of SS-2 |
夹芯板在爆炸载荷作用下的动态响应与其结构参数及载荷参数密切相关。本节主要讨论上面板厚度、芯层高度及炸药当量对其变形模式及能量吸收的影响。
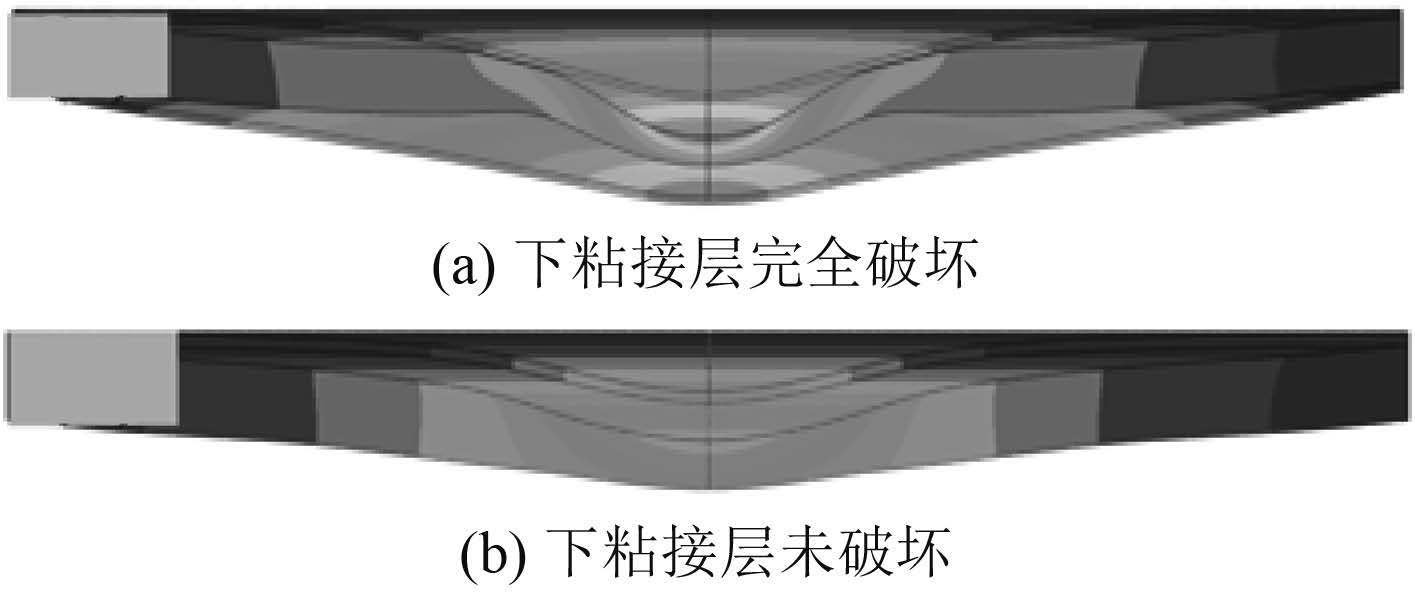
2.2.1 面板变形本文所研究范围内,夹芯板上粘接层均发生了破坏,部分工况下粘接层完全破坏,其余工况下粘接层未发生破坏,2 种情况变形模式如图 6 所示。
|
图 6 下粘接层完全破坏和下粘接层未破坏 Fig. 6 Bottom cohesive layers failed and bottom cohesive layers didn’t fail |
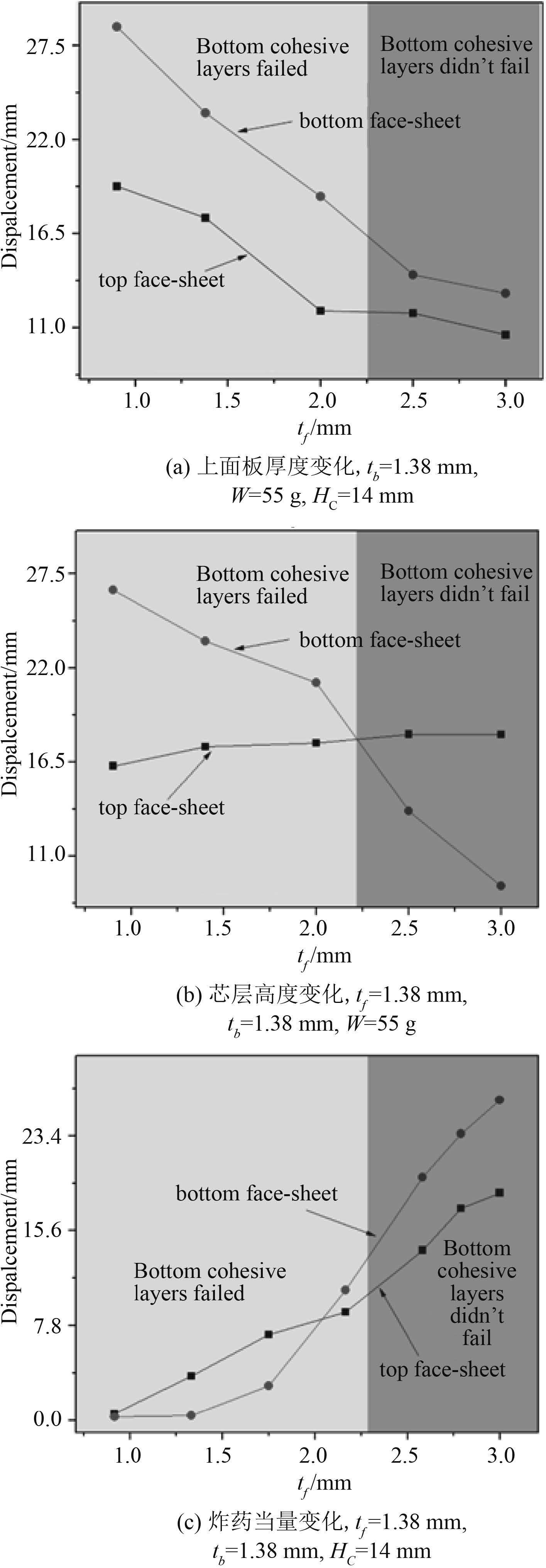
图 7 给出了不同工况下,夹芯板面板中心点最终挠度大小。从图 7 可以看出,在研究范围内,夹芯板下面板残余变形随着上面板厚度、芯层高度的增大而减小,随着炸药当量的增大而增大;上面板变形随着上面板厚度的增大而减小,随着芯层高度、炸药当量的增大而增大。计算结果表明,增加上面板厚度在一定程度上可以提高夹芯板的抗冲击性能,如图 7(a)所示。这是由于上面板厚度的增加,使得上面板刚度增加,导致其上面板变形减小,这也使得芯层压缩量减小,传递到下面板的能量也随之减小,下面板的变形也因此减小。下粘接层的失效也与下面板变形大小密切相关,当上面板厚度大于 2 mm 时,下面板变形下降,使得下粘接层不再产生破损。
|
图 7 夹芯板面板中心点最终挠度随不同参数的变化 Fig. 7 The deflection of the center in the face sheet of sandwich panel versus parameters |
图 7(b)表明,芯层高度的增加使得上面板变形量线性增大,同时下面板变形线性减小。从图中可以观察到,芯层高度的改变对下面板变形的影响较为明显,因此,在布置空间允许的前提下,增加芯层高度可以以增加较小结构质量为代价来显著提高夹芯板的抗爆性能。从图 7(c)可以看出,上面板位移随着炸药当量的增大而线性增加,在炸药当量较小时,下面板没有明显变形,当炸药当量大于 20 g 之后,下面板变形线性增加,并在炸药当量大于 40 g 之后,下面板变形大于上面板变形,且伴随着下粘接层的破坏。
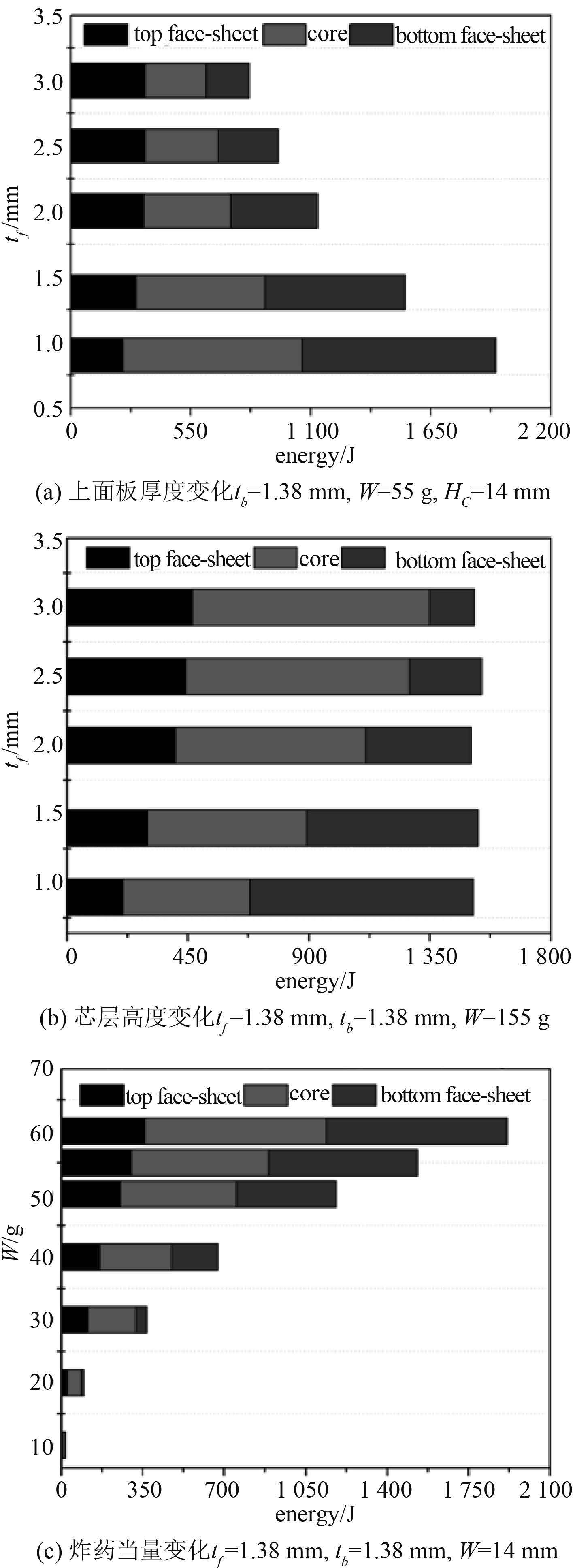
2.2.2 能量吸收图 8 给出了不同工况下,夹芯板面板及芯层的能量吸收情况。从图 8(a)可以看出,随着上面板厚度的增加,夹芯板总体吸能减少,这是由于上面板厚度的增加,提高了上面板的质量。文献[16]给出了夹芯板在爆炸载荷作用下获得的初始动能计算公式:
| ${{W}_{D}}=\frac{{{I}^{2}}}{{{m}_{f}}},$ | (3) |
其中 I 为炸药载荷作用在结构上的冲量,mf 为夹芯板上面板质量。当上面板质量增大会使得夹芯板获得的初始动能减少,这也使得夹芯板最终所耗散的能量减少。上面板厚度的增加,也导致了上面板变形的减小,这使得芯层压缩量及背面板变形减小,上面板的整体吸能比重增大,上面板成为主要承受爆炸载荷的构件。
当上面板厚度不变的情况下增加芯层高度,夹芯板的总体吸能量几乎保持不变,如图 8(b)所示。这是由于在这种情况下,夹芯板前面板厚度未发生变化,因此夹芯板获得的初始动能保持不变,所耗散的总能量也没有改变。随着芯层高度的增加,上面板变形及芯层压缩量增大,下面板变形减小,导致上面板及芯层的吸能比增加,下面板吸能比减少。
|
图 8 夹芯板面板和芯层的能量吸收情况 Fig. 8 Energy absorbed by face sheets and core of sandwich panels |
图 8(c)表明,炸药当量的增加会导致夹芯板的总体吸能量的增加。当炸药当量小于 50 g 时,芯层为结构主要吸能构件,此时夹芯板的芯层压缩变形占能量吸收的主导作用;当炸药当量大于 50 g 时,随着炸药当量的增加,芯层吸能量没有发生明显变化,下面板转变为主要吸能构件,此时夹芯板面板的整体弯曲变形占能量吸收的主导作用。
3 结 语针对 PVC 夹芯板在空爆载荷作用下的动响应建立了有限元数值模型,并通过实验结果验证了有限元模型的有效性。继而,分析了夹芯板上面板厚度、芯层高度及炸药当量对其抗爆性能的影响,得到如下结论:
1)PVC 夹芯板在爆炸载荷作用下的变形模式主要表现为上面板局部弯曲变形、芯层压缩及下面板整体弯曲变形,并通过结构变形耗散能量。
2)数值结果表明,夹芯板的动态响应与上面板厚度、芯层高度和炸药当量密切相关,增加上面板厚度或芯层高度均能明显降低下面板挠度,从而提高其抗爆性能。在炸药当量较小时,夹芯板的变形以上面板弯曲及芯层压缩为主,下面板变形较小;对于本文所研究工况,当炸药当量大于 30 g 时,下面板变形随着炸药当量的增加而线性增大。
3)夹芯板总体吸能量大小与上面板厚度密切相关,与芯层高度没有明显关联,上面板厚度越小,结构总体吸能量越大。上面板吸能占比随着上面板厚度的增加而增加;芯层吸能占比随着芯层高度的增加而增加。当炸药当量较小时,芯层为结构主要吸能构件;当炸药当量大于 50 g 时,随着炸药当量的增加,芯层吸能量没有发生明显变化,同时,下面板转变为结构主要吸能构件。
| [1] |
敬霖, 王志华, 赵隆茂. 多孔金属及其夹芯结构力学性能的研究进展[J]. 力学与实践 , 2015, 37 (1) :1–24.
JING Lin, WANG Zhi-hua, ZHAO Long-mao. Advances in studies of the mechanical performance of cellular metals and related sandwich structures[J]. Mechanics in Engineering , 2015, 37 (1) :1–24. |
| [2] |
赵桂平, 卢天健. 多孔金属夹层板在冲击载荷作用下的动态响应[J]. 力学学报 , 2008, 40 (2) :194–206.
ZHAO Gui-ping, LU Tian-jian. Dynamic response of cellular metallic sandwich plates under impact loading[J]. Chinese Journal of Theoretical and Applied Mechanics , 2008, 40 (2) :194–206. |
| [3] |
宋延泽, 王志华, 赵隆茂, 等. 泡沫金属子弹冲击下多孔金属夹芯板动力响应研究[J]. 兵工学报 , 2011, 32 (1) :1–7.
SONG Yan-ze, WANG Zhi-hua, ZHAO Long-mao, et al. Investigation on dynamic response of sandwich plate to the impact of cellular metallic projectile[J]. Acta Armamentarii , 2011, 32 (1) :1–7. |
| [4] |
敬霖, 王志华, 宋延泽, 等. 泡沫金属子弹撞击载荷下多孔金属夹芯板的动态响应[J]. 振动与冲击 , 2011, 30 (12) :22–27.
JING Lin, WANG Zhi-hua, SONG Yan-ze, et al. Dynamic response of a cellular metallic sandwich panel subjected to metal foam projectile impact[J]. Journal of Vibration and Shock , 2011, 30 (12) :22–27. |
| [5] | SIMULIA D. ABAQUS 6.11 analysis user's manual[M]. ABAQUS, 2011. |
| [6] | CHUNG KIM YUEN S, LANGDON G S, NURICK G N, et al. Response of V-shape plates to localised blast load: experiments and numerical simulation[J]. International Journal of Impact Engineering , 2012, 46 :97–109. DOI:10.1016/j.ijimpeng.2012.02.007 |
| [7] | LEE S, BARTHELAT F, HUTCHINSON J W, et al. Dynamic failure of metallic pyramidal truss core materials-experiments and modeling[J]. International Journal of Plasticity , 2006, 22 (11) :2118–2145. DOI:10.1016/j.ijplas.2006.02.006 |
| [8] | WEI X D, TRAN P, DE VAUCORBEIL A, et al. Three-dimensional numerical modeling of composite panels subjected to underwater blast[J]. Journal of the Mechanics and Physics of Solids , 2013, 61 (6) :1319–1336. DOI:10.1016/j.jmps.2013.02.007 |
| [9] | DESHPANDE V S, FLECK N A. Isotropic constitutive models for metallic foams[J]. Journal of the Mechanics and Physics of Solids , 2000, 48 (6/7) :1253–1283. |
| [10] | DANIEL I M, RAJAPAKSE Y D S. Major accomplishments in composite materials and sandwich structures[M]. Netherlands: Springer, 2010 : 818 . |
| [11] | FLECK N A, DESHPANDE V S. The resistance of clamped sandwich beams to shock loading[J]. Journal of Applied Mechanics , 2004, 71 (3) :386–401. DOI:10.1115/1.1629109 |
| [12] | LANGDON G S, KARAGIOZOVA D, Von KLEMPERER C J, et al. The air-blast response of sandwich panels with composite face sheets and polymer foam cores: experiments and predictions[J]. International Journal of Impact Engineering , 2013, 54 :64–82. DOI:10.1016/j.ijimpeng.2012.10.015 |
| [13] | Century Dynamics. AUTODYN theory manual, revision 4.3[M]. Concord, CA: Century Dynamics Inc, 2005 . |
| [14] | SUNDARAMURTHY A, ALAI A, GANPULE S, et al. Blast-induced biomechanical loading of the rat: an experimental and anatomically accurate computational blast injury model[J]. Journal of Neurotrauma , 2012, 29 (13) :2352–2364. DOI:10.1089/neu.2012.2413 |
| [15] |
张攀. 空中近场爆炸载荷下夹层板结构的动力学行为及其失效机理研究[D]. 武汉: 华中科技大学, 2014.
ZHANG Pan. Research on dynamic response and failure mechanism of sandwich plate structures under near-field air blast loading[D]. Wuhan: Huazhong University of Science and Technology, 2014. |
| [16] | ZHU F, ZHAO L M, LU G X, et al. Structural response and energy absorption of sandwich panels with an aluminium foam core under blast loading[J]. Advances in Structural Engineering , 2008, 11 (5) :525–536. DOI:10.1260/136943308786412005 |
 2016, Vol. 38
2016, Vol. 38
