2. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. Harbin Engineering University, Harbin 150001, China
人类最早使用双体船是由于发现将 2 艘船横向连接在一起,可以从内河到海上航行而不容易翻船,早期曾将这种方法用在帆船上,建造了双体帆船,这种帆船在海上可以承受较大的风浪。在此基础上,人们又发现双体船与同样吨位的单体船相比,具有更大的甲板面积和舱容[1],因此而被用于货船。20 世纪 60 年代后,随着海上高速船舶运输业的迅速发展,高速双体船由于其甲板面积宽大、舱容大而被普遍看好,成为近几十年来高性能船舶中应用最广、发展最快、建造数量最多的一种[2]。
典型的双体船由 2 个瘦长的片体组成,上部用连接桥连接。由于其特殊的连接桥结构,容易在甲板处形成角隅。因此对于双体船而言,角隅处的结构应力就显得相当关键。
本文使用谱分析方法[3-4]对双体船角隅处的疲劳强度进行分析研究,并对角隅处常用的优化方法进行分析比较,得到的结论对双体船乃至其他船型的相似角隅结构处的疲劳强度有一定的参考价值。
1 船体有限元模型建立目标船属于小尺度双体船,且船体细长。使用大型商业有限元软件 Msc.Patran/Nastran 对双体船进行有限元建模和计算分析。有限元模型采用右手坐标系,原点设于尾垂线和基线相交处,x轴为沿纵向船首方向为正,y 轴沿水平方向向左舷为正,z 轴沿垂向由原点向上为正。所有船体外板、纵横舱壁、甲板、平台和主要支撑构件等均在模型中予以表达。全船有限元模型如图 1 所示。

|
图 1 全船有限元模型图 Fig. 1 FEM model of the ship hull |
目前各国船级社提出的疲劳强度评估方法主要可分为简化计算法和直接计算法[5, 6]。在简化算法中,采用简化公式计算疲劳载荷和应力;或者采用简化公式计算载荷,应力由有限元法直接计算得出。而在直接算法中,则采取波浪载荷程序直接计算载荷,用有限元法直接计算结构应力。然后采用设计波的方法或谱分析法进行疲劳累积损伤的计算。目前的很多研究结果表明,根据不同船级社的简化疲劳评估方法,计算得到的结果差异一般都很大。而采用基于谱分析的疲劳评估直接计算法工作量十分巨大,且技术要求高。目前,船体结构的疲劳评估的研究方法还不能完全令人满意,仍需要对许多方面进一步研究探讨。但可以确定的是,直接计算法由于其基于谱分析方法的特性,具有最为清晰的物理含义,且过程合理。因此,一个合理统一的疲劳评估方法可以从基于谱分析的直接计算方法基础上发展。而本文的研究也是使用谱分析方法进行研究。
疲劳评估方法中的谱分析法是相对于基于 Miner 线性累积损伤原理和 S-N 曲线的简化方法而言的。在船舶结构的所有疲劳评估方法中,谱分析法被认为是最合理、最精确的。它建立在真实的海况及装载基础上,涉及复杂的水动力计算和有限元分析,考虑了不同的波频、航向和装载组合后的上百种工况,计算量大,计算周期长。双体船作为一种非常规船型,应用谱分析方法可以尽可能准确评估关键节点的疲劳寿命。
设
| $\[{{G}_{XX}}\left( \omega \right)={{\left| H\left( \omega \right) \right|}^{2}}{{G}_{\eta \eta }}\left( \omega \right),\]$ | (1) |
式中:
考虑
| $\[\begin{align} & D=\frac{{{T}_{d}}}{{\bar{a}}}\Gamma (1+\frac{m}{2})\sum\limits_{n=1}^{{{N}_{load}}}{{{p}_{n}}\cdot \sum\limits_{i=1}^{{{n}_{S}}}{\sum\limits_{j=1}^{{{n}_{H}}}{{{p}_{i}}{{p}_{j}}{{\nu }_{ijn}}}}{{\left( 2\sqrt{2{{m}_{0ij}}} \right)}^{m}}} \\ & =\frac{{{\nu }_{0}}{{T}_{d}}}{{\bar{a}}}\Gamma (1+\frac{m}{2})\sum\limits_{n=1}^{{{N}_{load}}}{{{p}_{n}}\cdot \sum\limits_{i=1}^{{{n}_{S}}}{\sum\limits_{j=1}^{{{n}_{H}}}{{{p}_{i}}{{p}_{j}}{{r}_{ijn}}}}{{\left( 2\sqrt{2{{m}_{0ij}}} \right)}^{m}}\le \eta } \\ \end{align}\]$ | (2) |
式中:Td 为船舶的设计疲劳寿命;D 为设计寿命期的疲劳累积损伤度;η 为利用系数,可接受的值定义为 η = 1;
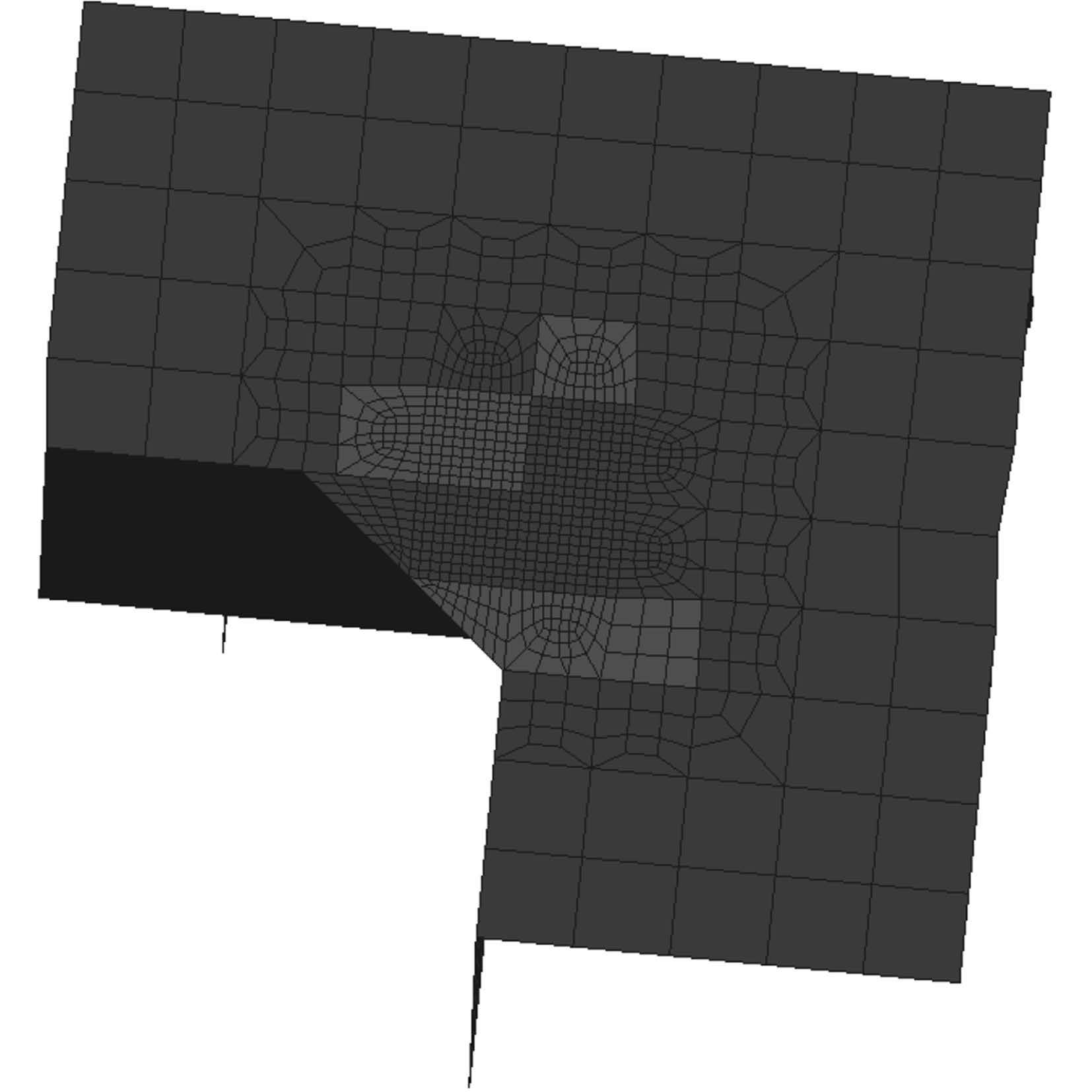
在双体船整船强度有限元分析的基础上,选择双体船上以下 4 个位置作为疲劳强度分析的热应力点: 船中附近连接桥侧封板与连接桥面板相交处、船中附近连接桥与船片体相交处、距船首 1/4L 处连接桥与船片体相交处、距船首 1/4L 处大开口角隅处。基于全船有限元模型,对这 4 个热点局部区域进行网格细化,得到局部精细化网格。通过热点位置细化单元的主应力值插值可以得到热点应力值。
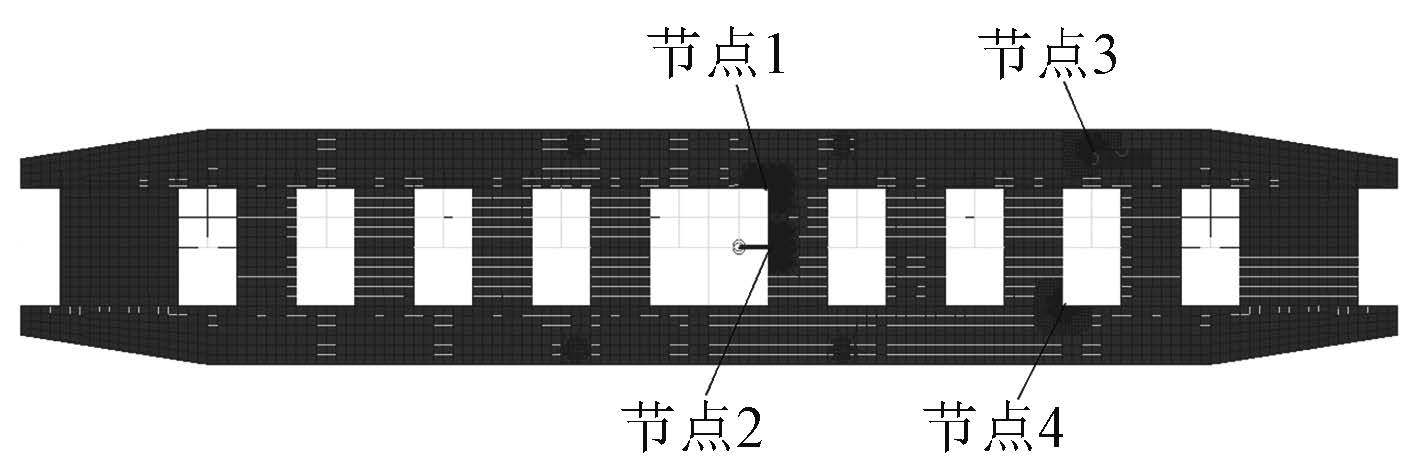
|
图 2 节点设置及细化模型 Fig. 2 Spots setting and the refined model |

|
图 3 角隅结构示意图 Fig. 3 Sketch map of corner structure |
波浪载荷是作用在船舶结构上的重要环境载荷之一。谱分析的步骤一般为:在计算得到多个浪向角和不同入射波频下船舶的运动响应及船舶水动压力之后,针对双体船航行状态进行疲劳强度评估分析。由此得到热点应力频响曲线并进行疲劳累积损伤计算。
在计算时,选取以下计算参数:船舶吃水为 1.2 m,航速取 0 kn。航向角选取范围为 0°~180°,间隔为 30°,并选定了 13 个波浪频率,具体计算工况参数见表 1。本船采用本船实际航行的渤海海浪散布图,该图覆盖了中国近海 B1 号海区。
|
|
表 1 计算工况参数表 Tab.1 Parameter table of calculating working condition |
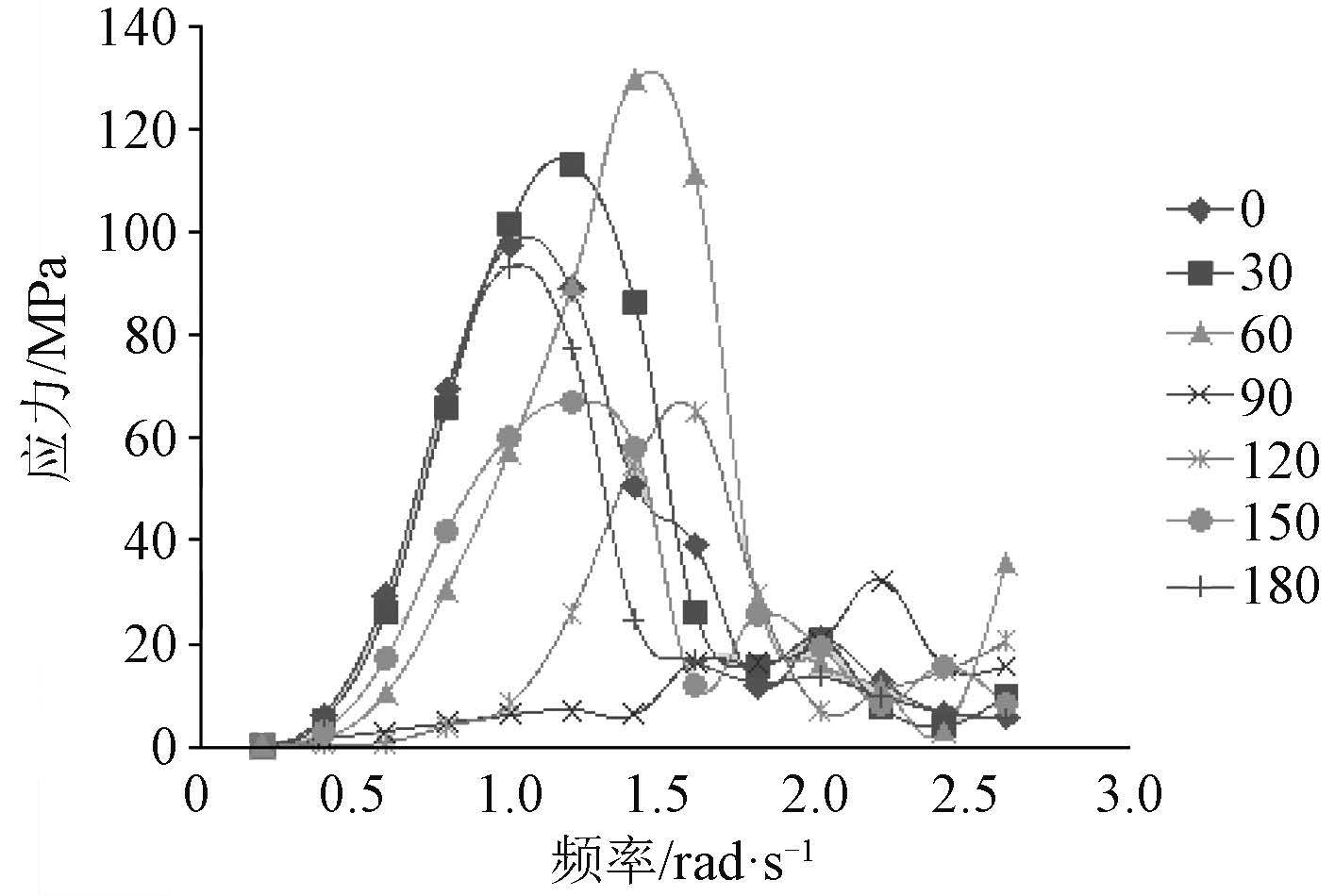
波浪载荷响应参数确定之后,利用波浪载荷计算程序 Compass-Walcs-Basic 进行水动力和结构响应计算,得到各规则波中的船体剖面载荷响应、运动响应及船体水动压力分布,总计算工况共计 182 个。在此基础上,计算各短期海况下各热点的应力值,各节点的热点应力传递函数曲线如图 4 ~ 图 7 所示。
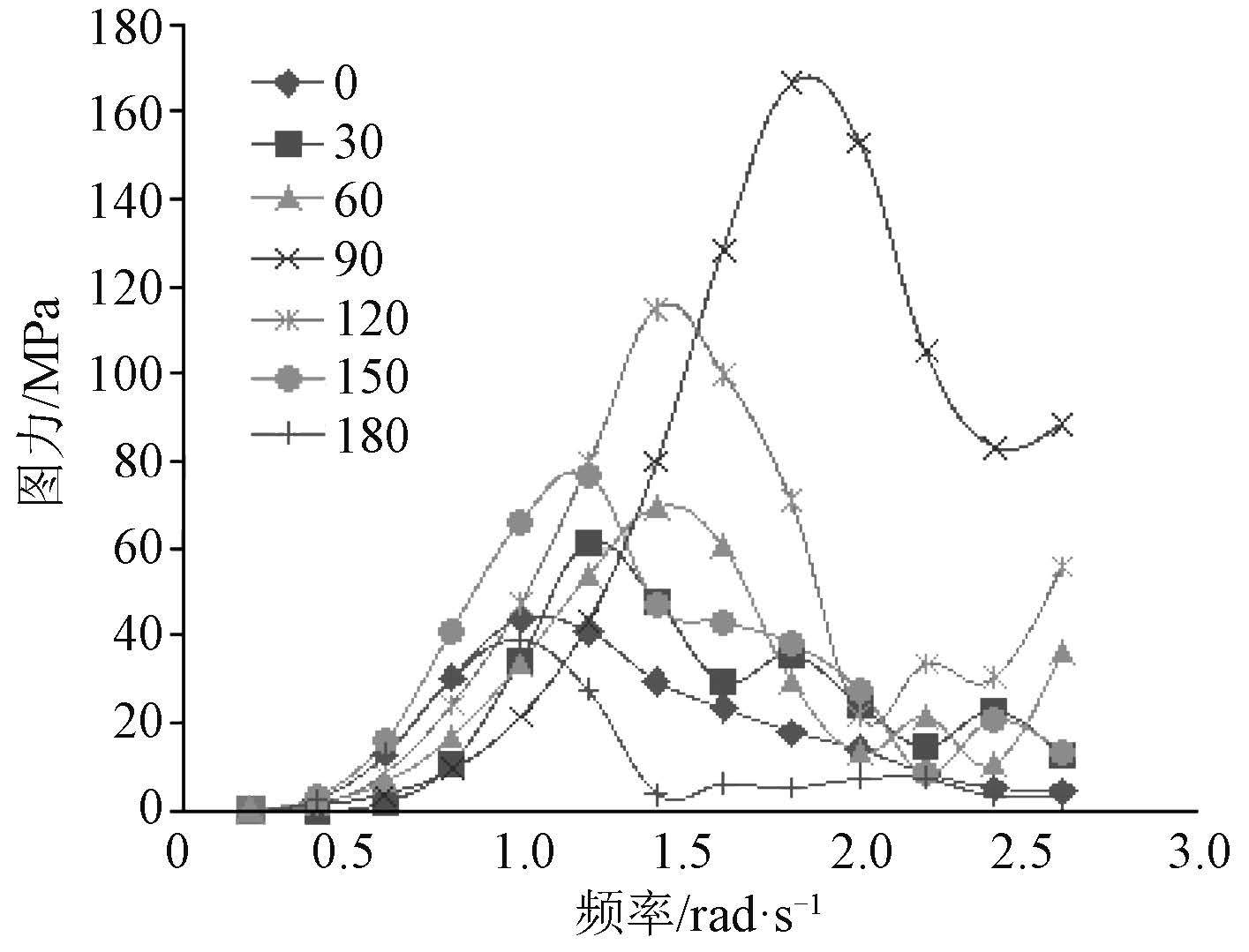
|
图 4 疲劳节点 1 应力响应传递函数 Fig. 4 Response transfer function of fatigue spot 1 |
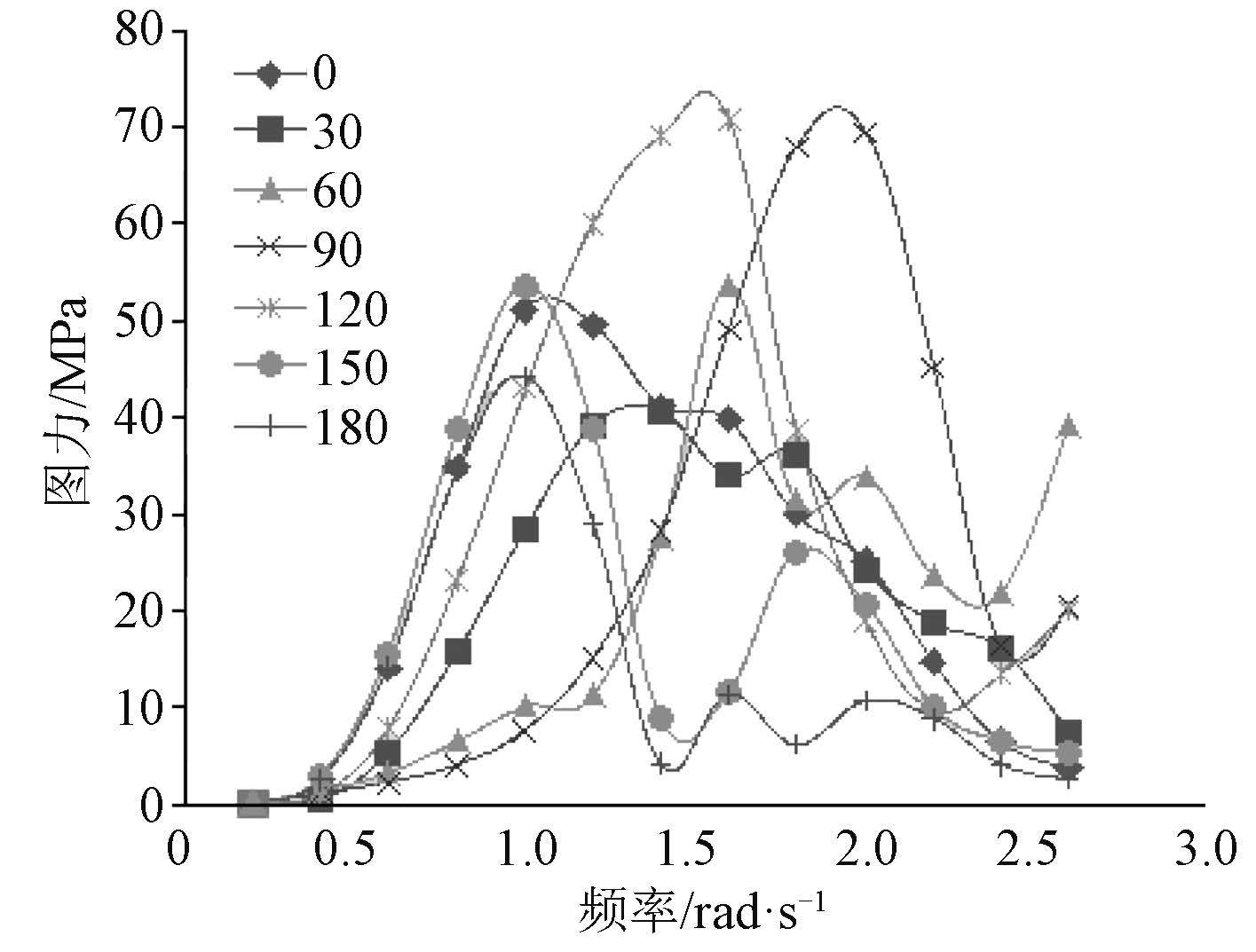
|
图 5 疲劳节点 2 应力响应传递函数 Fig. 5 Response transfer function of fatigue spot 2 |
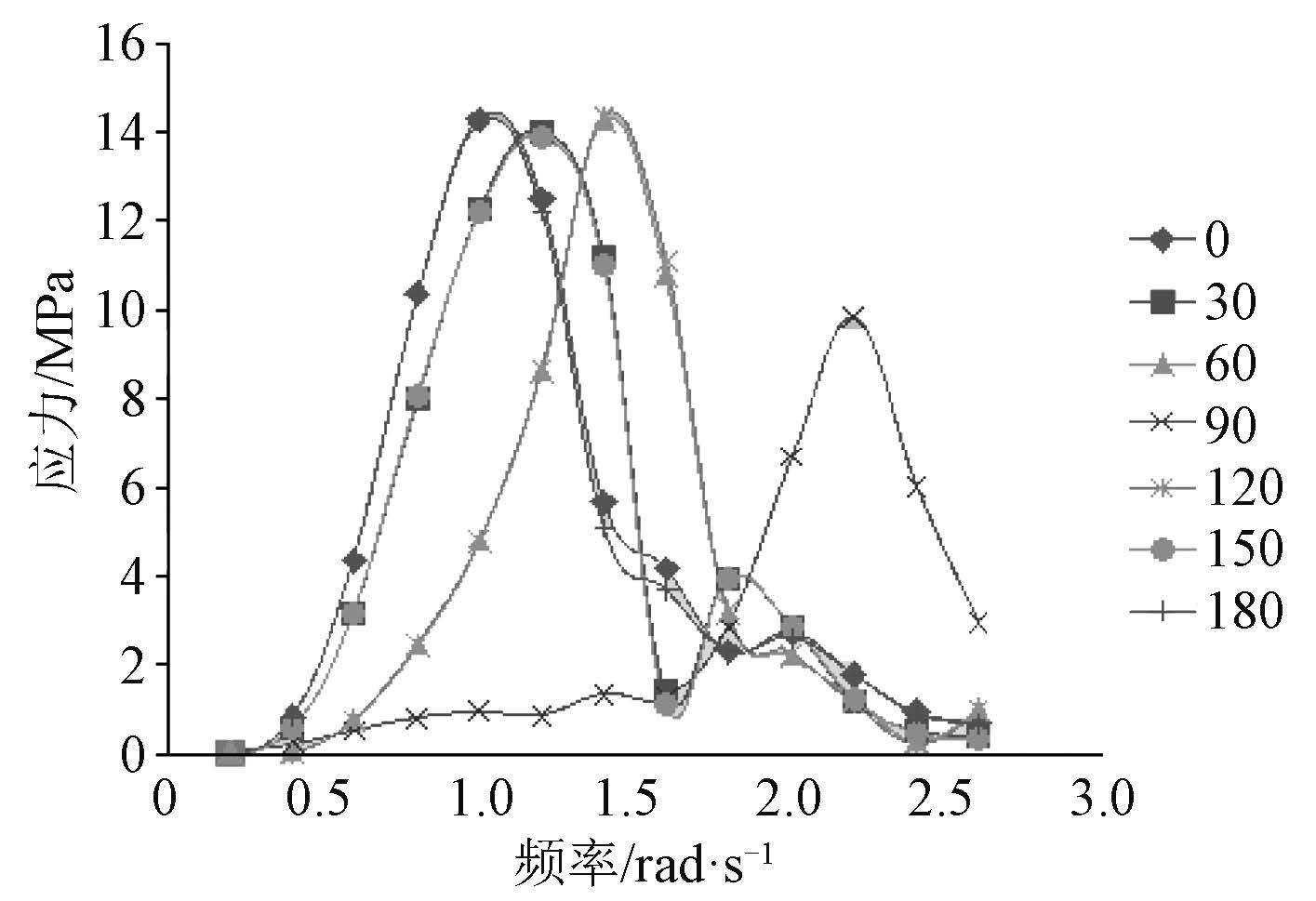
|
图 6 疲劳节点 3 应力响应传递函数 Fig. 6 Response transfer function of fatigue spot 3 |
|
图 7 疲劳节点 4 应力响应传递函数 Fig. 7 Response transfer function of fatigue spot 4 |
由于谱分析方法的计算工况比较多,若按操作界面中的处理方法提取应力不太现实。在这里采用 PCL 语言自动提取[7-8]的解决方案。
目标船舶的设计寿命取为 10 年,疲劳寿命计算采用 CCS《船体强度疲劳强度指南》中给出的 S-N 曲线。按照公式 2 对各疲劳节点进行疲劳累积损伤度和疲劳寿命计算,结果见表 2。
|
|
表 2 计算点的疲劳累积损伤度 Tab.2 The accumulated fatigue damage of the calculating spots |
由于角隅 2 的疲劳寿命为 420 年,符合双体船对疲劳强度的要求。因此,在后续的研究中不考虑此角隅节点。
4 角隅疲劳优化设计常见的角隅优化方法主要包括圆弧化、增加角隅附近板厚、增设肘板等。
由于双体船具有特殊的连接桥结构,其角隅大多由相互垂直的 2 个围壁形成。因此想要圆弧过渡需要将围壁曲化,对结构改动较大,不利于加工建造,因此本文主要考虑后 2 种角隅优化方法。
4.1 板厚对角隅疲劳强度的影响为了比较角隅附近主要受力板在角隅疲劳强度性能中扮演的角色,对厚度的研究分为主要受力板单独加厚与节点附近受力板全部加厚 2 个方案。为了保证疲劳强度计算一致,每次计算时有限元精细网格的边长需与主要受力板板厚在数值上保持一致。
由全船屈服应力与屈曲应力计算结果可以得到以下结论:节点 1 主要是纵向构件受力,受力最严重的是甲板;节点 3、4 主要是横向构件受力,受力最严重的是舱壁。
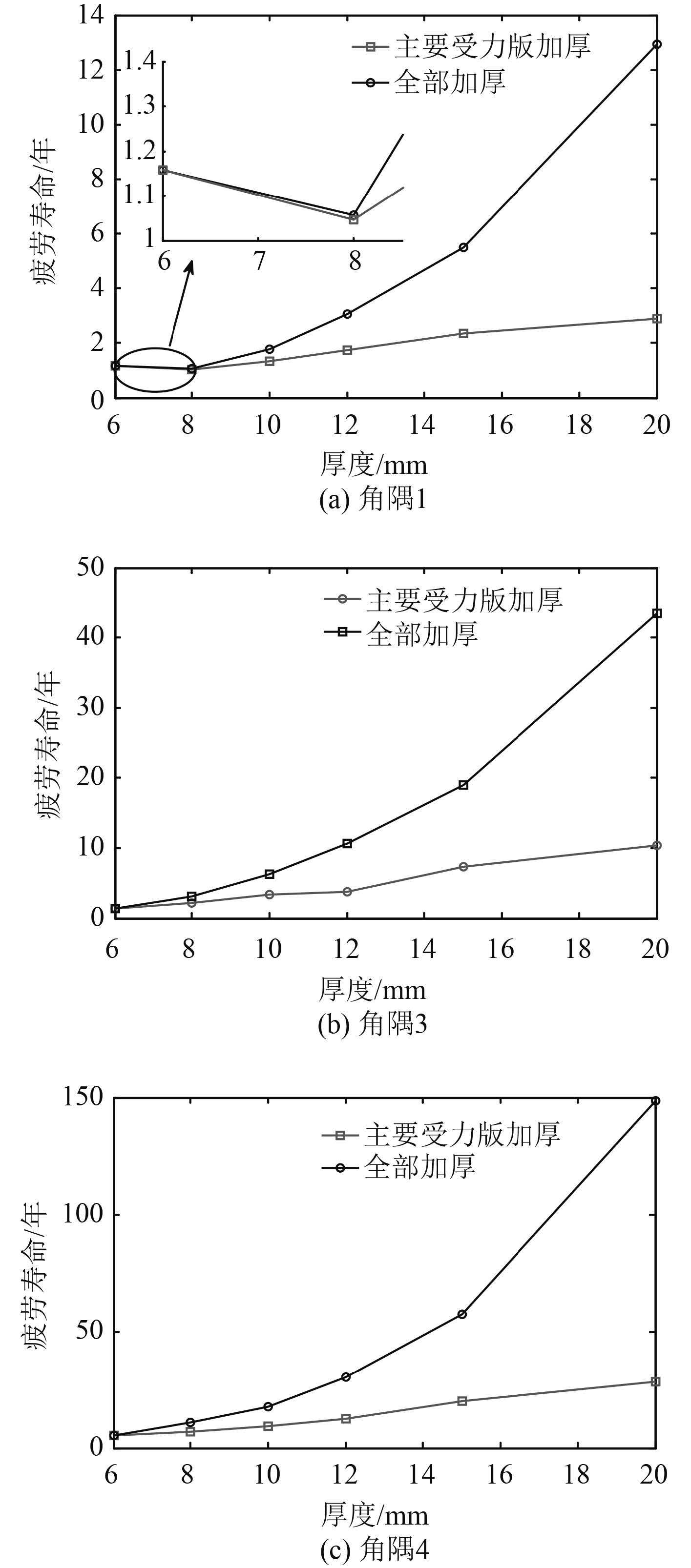
按照前述的方法对角隅附近板逐步进行加厚,得到加厚之后的疲劳累积损伤及疲劳寿命如表 3 所示。
|
|
表 3 板厚对角隅疲劳强度的影响 Tab.3 influence of the plate depth to the corner’s fatigue strength |
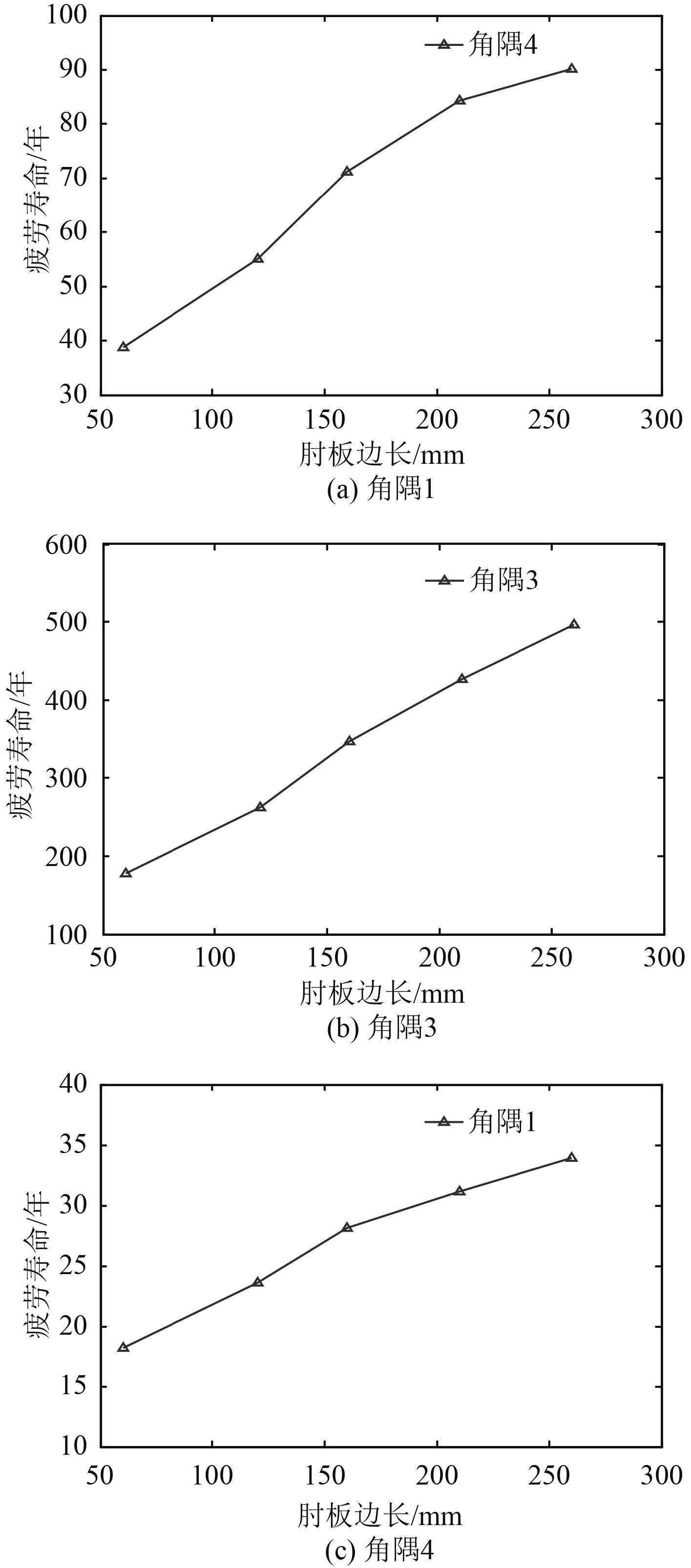
肘板对角隅疲劳强度的影响研究,主要从肘板的尺寸方面来考虑。肘板形式如图 10 所示。通过改变肘板的尺寸,得到不同尺寸肘板对角隅疲劳强度的影响结果如表 4 所示。
|
图 8 疲劳寿命与结构板厚的关系 Fig. 8 The relationship of fatigue life with the structure plate depth |
|
图 9 增设肘板角隅示意图(肘板边长为 120 mm) Fig. 9 Sketch map of the corner with bracket |
|
图 10 疲劳寿命与肘板边长的关系 Fig. 10 The Relationship of Fatigue Life with Bracket Length |
|
|
表 4 肘板尺寸对角隅疲劳强度的影响 Tab.4 The influence of bracket size to the fatigue strength of the corners |
1)随着角隅附近板厚的增加,角隅处疲劳强度也随之增加。但角隅疲劳强度对板厚的敏感度不强,如果角隅处疲劳强度性能不好时为满足使用要求通常需要增加许多厚度,这样容易导致构件失去其原本的功能;
2)由角隅 1 厚度与疲劳强度的关系发现,角隅各受力板的耦合作用十分明显,小幅增厚主要受力板或者周围结构板可能不能使疲劳强度增加,在结构设计时应注意避免这种问题;
3)单独增加主要受力板厚度的效果不如整体增加角隅附近结构板厚理想;
4)增设肘板是增加角隅处疲劳强度最直接的办法。但有些情况下,增设肘板会对结构形式造成不利影响。因此可以根据实际情况对 2 种方法进行选择;
5)随着肘板尺寸的增加,疲劳强度也会随之增加。可以通过计算,对肘板尺寸进行设计,以节省成本。
| [1] |
吴先彪. 40米钢制双体客船强度直接计算分析[D]. 厦门: 集美大学, 2014.
WU Xian-biao. The direct calculation and analysis for the strength of a 40m steel passenger catamaran[D]. Xiamen: Jimei University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10390-1014358943.htm |
| [2] |
程相如. 双体船结构强度计算[D]. 大连: 大连理工大学, 2012.
CHENG Xiang-ru. The structure strength calculation of catamaran[D]. Dalian: Dalian University of Technology, 2012. http://epub.cnki.net/kns/detail/detail.aspx?QueryID=39&CurRec=1&recid=&FileName=1012394215.nh&DbName=CMFD2012&DbCode=CMFD&pr= |
| [3] |
冯国庆. 船舶结构疲劳强度评估方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
FENG Guo-qing. Research on fatigue strength assessment method of ship structures[D]. Harbin: Harbin Engineering University, 2006. http://epub.cnki.net/kns/detail/detail.aspx?QueryID=43&CurRec=1&recid=&FileName=2007119442.nh&DbName=CDFD9908&DbCode=CDFD&pr= |
| [4] |
徐志亭. 小水线面双体船结构疲劳分析及典型节点优化研究[D]. 上海: 上海交通大学, 2012.
XU Zhi-ting. Structural fatigue analysis and typical local details optimization research of SWATH[D]. Shanghai: Shanghai Jiaotong University, 2012. http://cdmd.cnki.com.cn/article/cdmd-10248-1012017798.htm |
| [5] |
陈颖, 岳亚霖, 崔维成. 小水线面双体船典型节点抗疲劳设计[J]. 舰船科学技术 , 2010, 32 (6) :8–13.
CHEN Ying, YUE Ya-lin, CUI Wei-cheng. Anti-fatigue design of SWATH typical local details[J]. Ship Science and Technology , 2010, 32 (6) :8–13. |
| [6] |
任慧龙, 张清越, 胡雨蒙, 等. 基于参数化子模型的SWATH船典型节点抗疲劳设计[J]. 舰船科学技术 , 2015, 37 (6) :11–15.
REN Hui-long, ZHANG Qing-yue, HU Yu-meng, et al. Anti-fatigue design of SWATH typical details based on parametric sub-model method[J]. Ship Science and Technology , 2015, 37 (6) :11–15. |
| [7] |
冯国庆, 刘相春, 任慧龙. 基于PCL语言的波浪压力自动加载方法[J]. 船舶力学 , 2006, 10 (5) :107–112.
FENG Guo-qing, LIU Xiang-chun, REN Hui-long. A PCL based automatic loading approach for wave pressures[J]. Journal of Ship Mechanics , 2006, 10 (5) :107–112. |
| [8] |
冯国庆, 任慧龙, 李辉, 等. 基于PCL的疲劳谱分析直接计算系统开发[J]. 船海工程 , 2006, 39 (5) :4–7.
FENG Guo-qing, REN Hui-long, LI Hui, et al. Development of the direct spectral fatigue analysis system based on patran command language[J]. Ship & Ocean Engineering , 2006, 39 (5) :4–7. |
 2016, Vol. 38
2016, Vol. 38
