柴油机作为舰船的主要动力装置,其性能的好坏对舰船的技战术性能有着很大影响,因此对其进行状态检测和故障诊断具有重要的意义。振动诊断方法由于其速度快、精度高、适用范围广、可实现在线监测诊断,且振动信号易于测取,一直是柴油机故障诊断的前沿和热点。但柴油机振动响应信号十分复杂,具有典型的非平稳和非线性特点,使振动诊断存在一定难度。究其原因是由于柴油机结构的复杂性,在工作过程中即包含有旋转运动,又有往复运动,激励源复杂且数量多,多变的边界条件及恶劣的工作环境。为了解决在故障诊断中面临的非平稳非线性信号的强耦合、弱故障特提取难题,国内外大量学者进行了深入的研究,大量的时频分析方法被提出,如短时傅里叶变换、S 变换、小波变换、WVD 时频分布、MHD 时频分布、HHT 时频分布[1-6]。这些方法的提出为处理非线性和非稳态信号提供了必要方法,但由于柴油机的循环波动性,形成的柴油机振动谱图像千差万别,就“如何提取振动谱图像中敏感特征,实现不同故障的自动识别诊断”,到现在还没有一个统一的认识。
鉴于此,本文提出一种基于图像的柴油机在线故障诊断方法。该方法直接将采集到的一维柴油机振动信号生成二维的小波包振动谱图像,通过对二维图像进行特征参数提取和分类,来实现对柴油机的智能故障诊断。最后将其应用到柴油机气门间隙的故障诊断实例中,可实现在线诊断。
1 小波包振动谱图像的生成根据柴油机工作机理,若某一元件出现损伤时,在柴油机负载运行过程中会撞击与之相互作用的其它元件表面,产生周期性的脉冲激励,因此,若柴油机出现故障,信息必然会直接在元件就近柴油机表面的振动信号中得以反映。振动谱图像的生成方法有以下几类:1)线性时频分析:短时傅里叶变换,小波变换,谱图等;2)二次型时频分布:WVD 时频分布、MHD 时频分布、S 变换时频分布等;3)改进的二次型时频分布:EMD-WVD 时频分布[7]、自适应最优核时频分布[8]等;4)伪相图、吸引子图、递归图等其他类型振动谱图。为实现在线诊断的实时性,本文选取运算速度较快的小波包时频分析来进行振动谱的图像生成。
小波包方法是对信号进行分析的一种方法,它具有对信号特征的自适应性,因而能够使低频和高频成分都达到很精细的程度,小波包分解通过正交镜像滤波器进行[9]。假设信号为 y(t),则有以下递推公式:
| ${{y}_{2n}}(t)=\sqrt{2}\sum{h(k){{y}_{n}}\left( 2t-k \right)},$ | (1) |
| ${{y}_{2n+1}}(t)=\sqrt{2}\sum{g(k){{y}_{n}}\left( 2t-k \right)}\circ $ | (2) |
其中:
信号经过小波包分解后,将分解结果在时频面上表示出来即小波包时频振动谱图。如果原离散信号的样本数为 N,则分解结果为时频面上 N 个面积为
然而小波包变换中,小波基一旦选定,在对信号的分析过程中是无法随着信号的变化而变化的。一般情况下,根据柴油机非平稳振动信号时频域的变化特性,按照
在柴油机振动故障诊断的过程中,不同的类型故障的振动信号往往生成的振动谱图像也具有不同的特征,如何提取振动谱图像的这些敏感特征参数,是柴油机故障诊断的难点,直接影响着故障诊断的识别准确率。针对提取振动谱图像单一特征参数、易遗失重要信息及诊断精度低等问题,提出用灰度共生矩阵提取图像的纹理特征作为小波包振动谱图像的特征参数方法。纹理作为一种区域特征,是对于图像各像元之间空间分布的一种描述。由于纹理能充分利用图像信息,无论从理论上或常识出发它都可以成为描述与识别图像的重要依据,与其他图像特征相比,它能更好地兼顾图像宏观性质与细微结构 2 个方面。
2.1 图像压缩在用灰度共生矩阵直接对生成的振动谱图像进行特征提取时,往往计算效率低下,耗时较长,难以满足在线故障诊断实时性的要求。究其原因是得到的振动谱图像维数较大,因此需要对得到的时频图像进行降维。文中选用的是运算速率相对较快,缩放质量较高的双线性内插值算法。
|
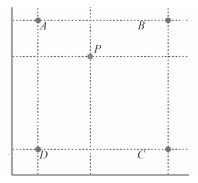
图 1 双线性内插值简图 Fig. 1 Schematic Diagram of Quadratic Interpolation Method |
双线性内插值是指缩放之后的图像像素坐标映射回原来的坐标空间时,如果出现了没有对应到整数点的情况,需要做 2 次线性的插值计算出新的坐标的像素值。设已知图像上单位正方形的 A,B,C,D 四个顶点值分别为
1)首先对上端的 2 个点进行线性插值
| $f(x,0)=f(0,0)+x[f(1,0)-f(0,0)];$ | (3) |
2)对下端的 2 个顶点进行线性插值
| $f(x,1)=f(0,1)+x[f(1,1)-f(0,1)];$ | (4) |
3)对垂直方向进行线性插值得到:
| $f(x,y)=f(x,0)+y[f(x,1)-f(x,0)];$ | (5) |
4)综合以上三式得最终的插值公式:
| $\begin{align} & f(x,y)=x[f(1,0)-f(0,0)]+y[f(0,1)-f(0,0)]+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ xy[f(1,1)+f(0,0)-f(1,0)]+f(0,0)\circ \\ \end{align}$ | (6) |
灰度共生矩阵[11]的定义为从图像灰度级为 i 的象元
| $\begin{align} & P(i,j,d,\theta )=\{({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})|f({{x}_{1}},{{y}_{1}})=i, \\ & f({{x}_{2}},{{y}_{2}})=j,\left| ({{x}_{1}},{{y}_{1}})-({{x}_{2}},{{y}_{2}}) \right|=d, \\ & \ \ \ \ \ \ \ \ \ \ \ \ \angle (({{x}_{1}},{{y}_{1}})-({{x}_{2}},{{y}_{2}}))=\theta \}\circ \\ \end{align}$ | (7) |
式中(x2,y2)为灰度级为 j 的象元。通常 d = {1,2,3,4},θ = {0°,45°,90°,135°}。
本文采用灰度共生矩阵的 11 个具有显著物理意义的特征参量用于纹理分析,进行特征提取:
1)二阶角矩。又称为能量,是图像灰度分布均匀程度和纹理粗细的一个度量。当图像较细致、均匀时,二阶角矩值较大,最大时为 1,表明区域内图像灰度分布完全均匀;反之,当图像灰度分布很不均匀、表面呈现出粗糙特性时,此时二阶角矩值较小。其数学表达式为:
| ${{f}_{1}}=\sum\limits_{i=1}^{{{N}_{g}}}{\sum\limits_{j=1}^{{{N}_{g}}}{{{P}^{2}}}(i,j,d,\theta )}\circ $ | (8) |
2)对比度。反映邻近象素的反差,是纹理定域变化的度量,可以理解为图像的清晰度、纹理的强弱。对比度值越大,表示纹理基元对比越强烈、纹理效果越明显;对比度值较小,表示纹理效果越不明显;当对比度值为 0,表明图像完全均一、无纹理。
| ${{f}_{2}}=\sum\limits_{n=0}^{{{N}_{g}}-1}{{{n}^{2}}}\left[ \sum\limits_{i=1}^{{{N}_{g}}}{\sum\limits_{j=1}^{{{N}_{g}}}{{{P}^{2}}}(i,j,d,\theta )} \right]\circ $ | (9) |
3)相关度。衡量共生矩阵在行或列方向上的相似程度,是灰度线性关系的度量。不同图像的相关值之间并无太大差异,而同一幅图像自身 4 个方向的相关值之间却往往存在较大的差异,一般表现为在纹理方向上的相关值明显高于其它方向的相关值。因此,相关可用来指明纹理的方向性。
| ${{f}_{3}}=\sum\limits_{i=1}^{{{N}_{g}}}{}\sum\limits_{j=1}^{{{N}_{g}}}{\left[ (i\times j)\times P(i,j,d,\theta )-{{\mu }_{x}}\times {{\mu }_{y}} \right]}/\left( {{\sigma }_{x}}\times {{\sigma }_{y}} \right)\circ $ | (10) |
式中:
4)熵、和熵及差熵。代表图像的信息量,是图像内容随机性的量度,指示纹理的复杂程度。当图像复杂程度高时,此时熵值最大,分形值也相对较高;当图像复杂程度低时,熵值较小或为 0。
和熵:
| ${{f}_{\text{4}}}=-\sum\limits_{k=2}^{2{{N}_{g}}}{{{P}_{x+y}}(k)\log \left[ {{P}_{x+y}}(k) \right]};$ | (11) |
熵:
| ${{f}_{\text{5}}}=-\sum\limits_{i=1}^{{{N}_{g}}}{\sum\limits_{j=1}^{{{N}_{g}}}{{{P}^{2}}(i,j,d,\theta )}}\log \left[ P(i,j,d,\theta ) \right];$ | (12) |
差熵:
| ${{f}_{\text{6}}}=-\sum\limits_{k=0}^{{{N}_{g}}-1}{{{P}_{x-y}}(k)\log \left[ {{P}_{x-y}}(k) \right]}\circ $ | (13) |
5)均值和。图像区域内像素点平均灰度值的度量,反映图像整体色调的明暗深浅。
| ${{f}_{\text{7}}}=\sum\limits_{k=2}^{2{{N}_{g}}}{k\times {{P}_{x+y}}(k)}\circ $ | (14) |
6)方差、方差和。反映纹理变化快慢、周期性大小的物理量。值越大,表明纹理周期越大。方差、方差和的值均随图像纹理的不同有较大的变异,可作为区分纹理的一个重要指标。
方差:
| ${{f}_{\text{8}}}=\sum\limits_{i=1}^{{{N}_{g}}}{\sum\limits_{j=1}^{{{N}_{g}}}{{{(1-u)}^{2}}P(i,j,d,\theta )}},$ | (15) |
其中 μ 为
方差和:
| ${{f}_{\text{9}}}=\sum\limits_{k=2}^{2{{N}_{g}}}{{{(k-{{f}_{\text{7}}})}^{2}}{{P}_{x+y}}(k)}\circ $ | (16) |
7)差的方差。表明邻近像素对灰度值差异的方差,对比越强烈,值越大;反之,值越小。
| ${{f}_{\text{10}}}=\sum\limits_{k=0}^{{{N}_{g}}-1}{\left[ k-\sum\limits_{k=1}^{{{N}_{g}}-1}{k\times {{P}_{x-y}}(k)} \right]}\times {{P}_{x-y}}(k)\circ $ | (17) |
8)逆差矩。反映纹理的规则程度。纹理杂乱无章、难于描述的,逆差矩值较小;规律较强、易于描述的,逆差矩值较大。
| ${{f}_{\text{11}}}=\sum\limits_{i=1}^{{{N}_{g}}}{\sum\limits_{j=1}^{{{N}_{g}}}{P(i,j,d,\theta )}}/\left[ 1+{{(i-j)}^{2}} \right]\circ $ | (18) |
这样由以上 11 个特征量,可以作为振动谱图像的纹理特征向量:
| $t=[{{f}_{1}},{{f}_{2}},{{f}_{3}},{{f}_{4}},{{f}_{5}},{{f}_{6}},{{f}_{7}},{{f}_{8}},{{f}_{9}},{{f}_{10}},{{f}_{11}}]\circ $ | (19) |
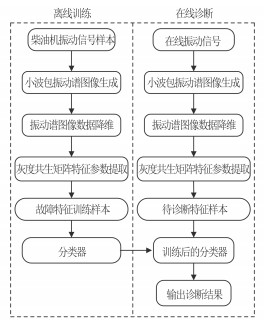
基于小波包振动谱图像的在线故障诊断方法,有以下几个步骤:首先采集柴油机典型故障的振动信号;用小波包时频分析方法对采集到的典型故障信号进行振动谱图像的生成;对生成的图像进行数据降维;使用灰度共生矩阵对得到的振动谱图像进行特征参数提取,并将其作为训练样本对智能分类器进行训练;有了训练好的分类器之后,就可以对在线采集的信号按照上述提取特征参数的方法构造待诊断故障样本并将其输入训练好的分类器,完成在线故障诊断。具体诊断过程如图 2 所示。
|
图 2 基于小波包振动谱图的柴油机在线故障诊断步骤 Fig. 2 Diesel Engine Online Fault Diagnosis Method Based on Wavelet Packet Vibration Image |
在柴油机工作过程中,进气阀会受到进气流的冷却作用,热负荷较小,故障发生率较低,而排气阀底部承受了极大的热负荷和交变冲击载荷,因而故障率较高,且不易对其进行检测,因此本文以排气阀作为研究对象。实验平台如图 3 所示,由 6135 型柴油机、传动轴、电机和控制台四部分组成。取柴油机 2 缸缸盖表面振动信号,采样频率 25 kHz,转速为 1 500 r/min,测试过程中,柴油机空载运行。气门间隙工况共设置以下 4 种:正常进、排气门间隙 0.3 mm、0.4 mm,排气门间隙过小为 0.06 mm,排气门间隙过大为 0.6 mm,严重漏气为开口 4 mm(长)× 1 mm(宽),如表 1 所示。实验共采集柴油机气门 4 种故障状态下各 60 种振动信号样本,总计 240 个。

|
图 3 试验平台 Fig. 3 Experimental Platform |
|
|
表 1 四种实验工况设置(单位:mm) Tab.1 Four states of IC engine’s valve train (mm) |
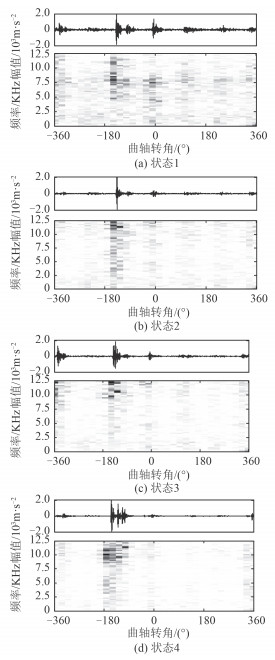
在选择小波基时,主要满足一定区间的紧支撑和足够的消失矩阶数,这样可以有效地表征振动信号的故障特征。Symlets 系列小波基是典型具有仅支撑性的正交小波基,并且拥有 N 阶消失矩阶数和近似对称的对称性,因此文中取 Symlets 小波基,分解层数为 6 层。分别取 4 种典型工况下信号进行小波包振动谱图像生成,结果如图 4 所示。
|
图 4 四种典型工况下的小波包振动谱图像 Fig. 4 Wavelet Packet Vibration Image for Four States |
在图 4 中,位于上方的是信号的时域波形图,位于下方的是小波包时频图,图中横坐标对应于曲轴的转角,纵坐标对应于频率,灰度值代表对应点的幅值大小。可以看出,不同气阀工况下的振动信号经小波包时频分析后,生成的振动谱图有较大差异,主要表现在位于曲轴转角 -340° 附近,-140° 附近的排气阀和进气阀关闭相继关闭引起的冲击,和位于曲轴转角 0° 附近,气体燃烧做工引起的冲击在时频平面上的灰度值的差异。因此通过小波包振动谱图生成,来对气门机构的状态进行识别可行。
4.3 振动谱图像数据降维上述生成的小波包振动谱图像的维数为 420 × 560,维数较大,经双线性内插值降维运算后维数为 42 × 56,大大减小了计算量,降维后图像如图 5 所示。图中横坐标表示列维数,纵坐标表示行维数,均为无量纲量,可以看出,使用双线性内插值算法对图像降维后,得到的振动谱图较好的保留了原始图像的敏感特征,有利于进一步特征提取。

|
图 5 数据降维后的小波包振动谱图像 Fig. 5 Wavelet Packet Vibration Images after Data Dimension Reduction |
对上述降维后得到的时频图像进行灰度共生矩阵的 11 个特征量提取。在灰度共生矩阵的提取中,灰度级 j = 50,距离 d = 2,角度 θ = 45°。由于文章篇幅有限,每种工况的特征参量展示 3 个,如表 2 所示。从表中可看出,同种工况间的数据大小比较接近,不同工况间的数据差别较大,说明该方法提取的特征参量有较好的分类特性。
|
|
表 2 降维和灰度级对振动谱图像识别耗时的影响(单位:s) Tab.2 Feature Parameters Extracted By Gray Level Co-Occurrence Matrix |
在对柴油机气门间隙四种典型工况进行分类时,选用最近邻分类器(KNNC)作为智能学习分类工具。首先从每一类故障样本中随机选取 30 个故障样本,共 120 个,进行小波包振动谱图像生成和特征参量提取,并用提取的特征参量组成训练集对分类器进行训练。为测试文中方法识别准确性,选用剩余的 120 个故障样本作为测试集,用训练好的分类器对其进行分类。为减小误差带来的影响,重复上述试验 10 次,取平均值作为最终的识别准确率结果。
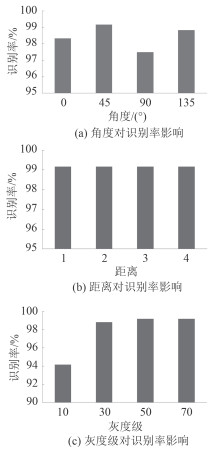
为进一步分析灰度共生矩阵参数选择对识别率的影响,首先取灰度级 j = 50,距离 d = 2,观察角度 θ 等于不同值时的识别准确率,结果如图 6(a)所示;然后取灰度级 j = 50,距离角度 θ = 45°,观察距离 d 取不同值时的识别准确率,结果如图 6(b)所示;最后取距离 d = 2,角度 θ = 45°,观察灰度级 j 取不同值时的识别准确率,结果如图 6(c)所示。
|
图 6 灰度共生矩阵不同特征参数对识别率影响 Fig. 6 The Influence of Gray Level Co-Occurrence Matrix Parameters to Recognition Rate |
从图 6 可看出,距离 d 的取值,对识别率几乎没有影响;角度 θ 的取值,对识别率的影响也比较小;对识别率影响较大的是灰度级 j 的取值。当 j 的取值过小,会丢失特征信息,造成识别率下降;随着 j 取值的增大,识别率随之上升,但计算量也随之增加,不利于在线诊断。因此,取距离 d = 2,角度 θ = 45°,观察灰度级 j 取不同值时的故障诊断消耗时间,如表 2 所示。故障诊断消耗时间从待诊断信号采集完成开始计时,到诊断完成计时停止,取振动谱图像降维与否进行对比。
从表 3 可看出,对振动谱图像降维后,特征提取识别消耗的时间大大小于降维前所耗时间;并且灰度级取值越大,计算量随之增大,消耗时间越长。因此合理选择灰度级的值,减小数据计算量,是实现在线诊断的关键。通过识别率和消耗时间综合考虑,本文通过数据降维,选取的灰度级 j = 50,距离 d = 2,角度 θ = 45°在识别精度达到 99.17% 的情况下仅耗时 0.24 S,可以满足在线诊断的要求。
|
|
表 3 采用灰度共生矩阵提取的特征参量 Tab.3 The Influence of Dimensionality Reduction and Gray Level to The Time Consuming (s) |
1)小波包振动谱图能够有效地反映柴油机气门间隙不同工况下时频分布特点,可用于对柴油机气门间隙故障的判别。
2)用双线性内插值算法对生成的振动谱图进行压缩,能够在极大较小计算量的同时保留图像的敏感信息。
3)用灰度共生矩阵对得到的振动谱图进行特征参数提取,并用分类器进行分类,完成故障诊断。将该方法应用于柴油机气门间隙的故障诊断中,结果表明,文中提出的基于小波包振动谱图像的柴油机在线故障诊断方法识别精度高,耗时短,适用于柴油机气门间隙的故障诊断,可实现舰船柴油机的在线监测诊断。
| [1] | DURAK L, ARIKAN O. Short-time Fourier transform: Two fundamental properties and an optimal implementation[J]. IEEE Transactions on Signal Processing , 2003, 51 (5) :1231–1242. DOI:10.1109/TSP.2003.810293 |
| [2] | DJUROVIĆ I, SEJDIĆ E, JIANG J. Frequency-based window width optimization for S-transform[J]. AEU-international Journal of Electronics and Communications , 2008, 62 (4) :245–250. DOI:10.1016/j.aeue.2007.03.014 |
| [3] | SMITH C, AKUJUOBI C M, HAMORY P, et al. An approach to vibration analysis using wavelets in an application of aircraft health monitoring[J]. Mechanical Systems and Signal Processing , 2007, 21 (3) :1255–1272. DOI:10.1016/j.ymssp.2006.06.008 |
| [4] | QAZI S, GEORGAKIS A, STERGIOULAS L K, et al. Interference suppression in the Wigner distribution using fractional Fourier transformation and signal synthesis[J]. IEEE Transactions on Signal Processing , 2007, 55 (6) :3150–3154. DOI:10.1109/TSP.2007.893971 |
| [5] | MARGENAU H, HILL R N. Correlation between measurements in quantum theory[J]. Progress of Theoretical Physics , 1961, 26 (5) :722–738. DOI:10.1143/PTP.26.722 |
| [6] | 王珍, 马孝江. 局域波时频法在柴油机缸套活塞磨损诊断中的应用研究[J]. 内燃机学报 , 2002, 20 (2) :157–160. |
| [7] | 蔡艳平, 李艾华, 王涛, 等. 基于 EMD-Wigner-Ville 的内燃机振动时频分析[J]. 振动工程学报 , 2010, 23 (4) :430–437. |
| [8] | 孙斌, 万鹏威, 陶达, 等. 基于自适应最优核时频分布的鸟类识别[J]. 数据采集与处理 , 2015, 30 (6) :1187–1195. |
| [9] | 葛哲学, 陈仲生. Matlab 时频分析技术及其应用[M]. 北京: 人民邮电出版社, 2006 . |
| [10] | 郭亚. 振动信号处理中的小波基选择研究[D]. 合肥: 合肥工业大学, 2003. |
| [11] |
郑红, 李钊, 李俊. 灰度共生矩阵的快速实现和优化方法研究[J]. 仪器仪表学报 , 2012, 33 (11) :2509–2515.
ZHENG Hong, LI Zhao, LI Jun. Study on fast implementation and optimal methodof gray level co-occurrence matrix[J]. Chinese Journal of Scientific Instrument , 2012, 33 (11) :2509–2515. |
 2016, Vol. 38
2016, Vol. 38
