2. 中国人民解放军92819部队, 辽宁 大连 116018
2. No.92819 Unit of PLA, Dalian 116018, China
毫米波频谱介于微波和红外波段之间,因此兼有微波和红外波段的优点。与微波相比,毫米波制导系统的绝对频带较宽,天线波束窄,旁瓣低,具有较高的制导精度和抗干扰性能;与红外相比,毫米波通过烟、雾、灰、尘的能力强,具有较好的全天候战斗能力;并且毫米波系统体积小、质量轻、易于高度集成化,是精确制导武器较为理想的频段。越来越多的反舰导弹采用了毫米波制导或毫米波参与下的复合制导技术。
水面舰艇的雷达截面积(RCS)是影响反舰导弹作战能力的重要因素,微波制导的反舰导弹就是靠检测舰艇 RCS 而导向目标的。由于目标的雷达散射特性与雷达的频率密切相关,现有以厘米波为主的舰艇雷达散射特性相关研究结论与应用,已不能适用于毫米波。研究水面舰艇的毫米波雷达散射特性,探讨水面舰艇毫米波 RCS 的评估方法,对水面舰艇的导弹攻击与防御作战均有重要的实际意义。
1 RCS 经验公式及其局限性20 世纪 70 年代,美国海军研究室目标特性部对海上舰船的雷达截面积进行了大量的实际测量。测量时使用 L,S,X 波段的微波雷达,以低倾角在贴近水面照射进行,按目标舷角每 2° 实测 1 组数据,共 180 个点,修正尖峰值后取平均值,得到了海上目标 RCS 的统计平均值估算公式,即被广泛应用的经验公式。
| ${{\sigma }_{\text{平均}}}=104\cdot {{f}^{0.5}}\cdot {{T}^{1.5}}\circ $ | (1) |
式中:σ平均为舰艇雷达截面积的总平均值,m2;f 为雷达频率,MHz;T 为目标舰艇满载排水量,kt。
利用该经验公式可对常规舰艇的 RCS 进行估算。但该公式的局限性也显而易见:仅适用于 L,S,X 等厘米波段,对毫米波段外推计算的适用情况还有待验证,不能直接用于水面舰艇毫米波雷达散射特性的研究。
2 水面舰艇雷达散射特性仿真原理随着仿真理论与技术的迅速发展,计算机仿真在各个领域均得到广泛应用。对于水面舰艇毫米波雷达散射特性的研究,可以通过仿真方法,首先模拟雷达电波的传播、散射机理,建立雷达工作的仿真模型并进行验证,然后在计算机上模拟各种条件,对水面舰艇的毫米波 RCS 进行仿真分析。
2.1 水面舰艇的雷达散射机理同一目标对于不同的雷达频率呈现不同的雷达截面积特征。当入射波波长远小于散射体本身和构成散射体各散射中心的尺寸时,目标雷达截面积就位于高频区。水面舰艇对毫米波末制导雷达的电磁散射基本上都是高频散射。在高频区域,目标的每一部分均可认为是独立地散射能量,而与其他各部分无关。这样,便可以将整艘舰艇分解为不同形状的散射单元集合,并根据各散射单元的形状特征和尺寸,分别计算各单元的散射场,组合形成舰艇的 RCS 特征。
高频散射主要包括,镜面散射、表面不连续性的散射(如边缘、拐角和尖顶)、表面导数不连续性的散射、爬行波或阴影边界的散射、行波散射、凹形区域的散射(如二面角、三面角)和相互作用散射(如多路径叠加或并排散射中心之间的多次往返) 7 种散射机理。将这些机理组合起来及可构成复合目标高频散射的总 RCS 特征。
2.2 水面舰艇 RCS 理论计算方法对于水面舰艇这样 RCS 较高的复杂目标,如果舰体结构设计为全封闭式,则只有镜面反射和表面不连续性的散射属于强散射机理,会显著影响舰艇的 RCS 特征,而其余 5 种都是弱散射机理,可忽略不计。在处理上述 2 种强散射机理时,常用的方法有几何光学法、物理光学法和几何或物理绕射理论方法等。
其中,几何光学法从射线追踪出发,在极高频的极限情况下,将麦克斯韦方程用光学定律来表达。当波长足够小,以至能量沿着射线路径流动时,光学原理规定了散射场的属性。几何光学的任务就是确定能量传播的路径,以及能量从远点传播到观测点的方式,具体计算场的振幅、相位和极化。
应用物理光学时,假设由物体上某一点对该物体其他点的散射场贡献和入射场强相比很小。同积分方程矩量解法一样,物理光学法的出发点是运用斯特拉顿—朱兰成散射场积分方程,在求解表面感应电流时,根据高频场的局部性原理,完全忽略各部分感应电流之间的相互影响,仅根据入射场独立地近似确定表面感应电流。
当必须考虑来自边缘、尖顶、拐角的散射场或阴影区内的散射场时,几何光学和物理光学都无法使用,必须利用几何或物理绕射理论来处理这一类绕射问题,依靠尖劈散射等典型结构的严格解来确定其绕射系数,把散射场表示为表面的物理光学贡献和边缘的绕射贡献之和,并利用二维尖劈问题的严格解来提取边缘贡献。
3 水面舰艇 RCS 仿真建模及验证 3.1 仿真建模1)建立 RCS 仿真计算模型
根据微波雷达的高频散射特点和水面舰艇的基本舰体结构特征,综合考虑镜面反射和表面不连续性的散射机理,运用几何光学法、物理光学法、几何绕射和物理绕射理论方法,建立水面舰艇 RCS 仿真模型。
2)建立水面舰艇三维模型
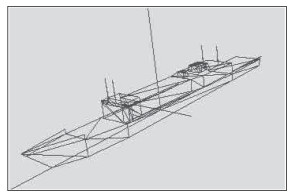
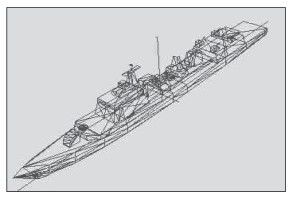
利用 Creator 三维制作软件,以“佩里”级导弹护卫舰和某型导弹驱逐舰为模板,建立 OpenFlight 格式的水面舰艇三维模型,作为仿真的舰艇模型输入。如图 1 和图 2 所示。
|
图 1 “佩里”级导弹护卫舰模型 Fig. 1 Model of Perry-class frigate |
|
图 2 某型导弹驱逐舰模型 Fig. 2 Model of a certain missile destroyer |
1)微波传播参数
根据水面舰艇的结构特点,设置微波在舰体的散射特征参数,包括电波返回接收机前,在舰艇各部位之间的反弹次数,以及允许进行绕射计算时尖顶或拐角的角度范围等。
2)雷达工作参数
根据反舰导弹末制导雷达的性能特点,设置雷达工作参数,包括雷达载频、极化方式、不同电波入射方位角、俯仰角计算目标雷达截面积值、振幅和相位数值等。
3)其他计算参数
入射方位角设置为:0°~359° 范围,1° 间隔。由于反舰导弹多为掠海飞行,因此仿真计算时设置电波俯仰角为 0°,这也符合经验公式中“低仰角”的测试条件,得到的仿真结果便于与经验公式进行比对。
3.3 仿真数据处理由于雷达电磁波到达目标后产生二次散射,散射波在某些相位上相互加强,导致雷达截面积在某些特定方位上的“突然越出”,这些越出的点并不能反映雷达截面积的整体特点。采用经验公式对越出点的处理方法,对计算结果进行峰值修正后,再计算 RCS 算术平均值。计算公式如下:
| $\text{ }\left\{ \begin{array}{*{35}{l}} {{\sigma }_{\text{平均}}}=(\sum\limits_{1}^{n}{{{10}^{\frac{RC{{S}_{i}}}{10}}}})/n, \\ RC{{S}_{\text{平均}}}=10\times \log ({{\sigma }_{\text{平均}}})\circ \\ \end{array} \right.$ | (2) |
式中,σ平均为 RCS 算术平均值,m2;RCSi 为仿真输出第 i 个方位角的 RCS 值,dB·m2;n 为输入的电波入射方位角的个数;RCS平均为 σ平均换算后的 RCS 平均值,dB·m2。
3.4 仿真模型验证分别以经验公式和仿真 2 种方法对舰艇的厘米波及毫米波 RCS 进行计算比对,以验证仿真模型的有效性及经验公式的外推可用性。
厘米波取 L、S、X 波段,其中心频率的典型值分别为 1.3 GHz,2.8 GHz,9.23 GHz。由于毫米波的大气传播衰减非常严重,末制导雷达应尽量选择在“大气窗口”工作,其典型波段为 Ka 波段,中心频率典型值为 35 GHz。
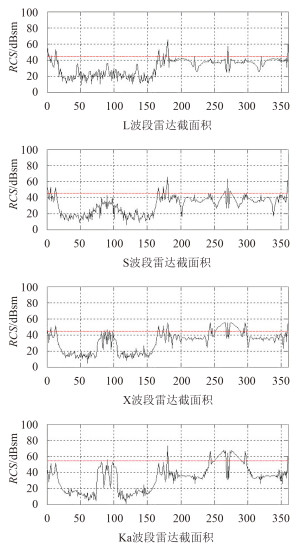
对“佩里”级导弹护卫舰 RCS 的仿真计算结果如图 3 所示。
|
图 3 “佩里”级导弹护卫舰雷达截面积仿真 Fig. 3 RCS simulation of Perry-class frigate |
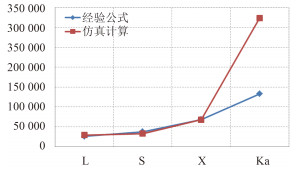
图中,横坐标为电波入射方位角,纵坐标为舰艇 RCS 值。以舰艇右正横为基准旋转一周,得到 RCS 曲线,横线为 RCS 仿真值的算术平均值 σ仿真。σ仿真与经验公式计算值σ经验的比对结果如图 4 和图 5 所示。通过比对,不难发现:
|
图 4 “佩里”级导弹护卫舰 RCS 计算比对 Fig. 4 RCS comparisons of Perry-class frigate |
|
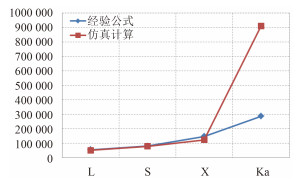
图 5 某型导弹驱逐舰 RCS 计算比对 Fig. 5 RCS comparisons of a certain missile destroyer |
1)厘米波段(L,S,X)2 种计算值相差不大。由于经验公式是在对海上目标进行大量实测得到的统计结果,计算比对结果表明仿真与实测基本相符。因此可认为仿真模型有效,可用于水面舰艇 RCS 的研究。
2)毫米波段(Ka)2 种计算值相差很大。由于仿真是基于水面舰艇的雷达散射机理进行建模,适用于任何雷达波段,且经过验证有效,计算比对结果表明经验公式在 Ka 波段的计算误差较大。因此可认为经验公式不能直接外推使用,仿真方法是获取水面舰艇毫米波 RCS 数据的有效途径。
4 水面舰艇毫米波 RCS 估算公式如果借鉴美海军研究室目标特性部对海上舰船 RCS 经验公式的处理方法,将大量仿真计算结果进行归纳总结,推导得出水面舰艇毫米波 RCS 的估算公式,可大大提高仿真方法的应用范围和灵活性。
通过仿真可以看出,雷达波长越短,舰艇 RCS 越大,且其加强程度随舰艇吨位增大而增大,舰艇 RCS 与雷达载频 f、目标吨位 T 之间是复杂的非线性关系。以 Ka 波段为突破进行分析,将水面舰艇 Ka 波段 RCS 分别与 L,S,X 波段 RCS 进行比对,如果用 Kj 表示二者的比值,那么 Kj 值应是 f 的递减函数、T 的递增函数。建立其他几型常规水面舰艇模型进行仿真计算,得到 Kj 与 f、T 的拟合关系如下:
| ${{K}_{j}}={{(\frac{{{f}_{ka}}}{f})}^{0.5}}\times {{T}^{0.7}},$ | (3) |
如果将 Kj 作为“毫米波修正系数”,与原 RCS 经验公式相乘,即可得到水面舰艇 Ka 波段 RCS 估算公式:
| ${{\sigma }_{Ka}}=104\times {{f}_{Ka}}^{0.5}\times {{T}^{2.2}}\circ $ | (4) |
该估算公式以传统 RCS 经验公式为基础,并依据大量仿真计算的统计结果进行修正,实现了 RCS 经验公式在 Ka 波段的外推使用。
5 结语仿真方法是获取水面舰艇毫米波 RCS 数据的有效途径,依据仿真方法获得的水面舰艇 Ka 波段 RCS 估算公式,具有较强的可操作性。应该指出,要想进一步提高仿真方法及估算公式的实际应用价值,还需进行大量的研究工作,包括更高精度的水面舰艇模型、海杂波模型、舰艇隐身涂层的电波传导模型,以及开展毫米波 RCS 的海上实测研究等。
| [1] |
余宏明, 张志坚. 毫米波雷达及其对抗[J]. 舰船电子工程 , 2007, 27 (2) :168–172.
YU Hong-ming, ZHANG Zhi-jian. Millimeter-wave radar and its countermeasures[J]. Ship Electronic Engineering , 2007, 27 (2) :168–172. |
| [2] |
肖芳, 周涛, 杨劲飞. 杂波对毫米波雷达 RCS 测量的影响[J]. 舰船电子对抗 , 2006, 29 (4) :57–59.
XIAO Fang, ZHOU Tao, YANG Jin-fei. Influence of clutter on RCS measurement in millimeter wave radar[J]. Shipboard Electronic Countermeasure , 2006, 29 (4) :57–59. |
| [3] |
胡守军. 毫米波多单元线散射体的雷达散射截面计算[J]. 红外与毫米波学报 , 1999, 18 (2) :163–166.
HU Shou-jun. RCS calculation for the multiple linear scattering units in millimeter waveband[J]. Journal of Infrared and Millimeter Waves , 1999, 18 (2) :163–166. |
| [4] |
马国忠, 韦高, 许家栋. 雷达目标的角闪烁及 RCS 的计算[J]. 系统工程与电子技术 , 1995, 17 (2) :14–20, 37.
MA Guo-zhong, WEI Gao, XU Jia-dong. Glint analysis and RCS computation for radar target[J]. Systems Engineering and Electronics , 1995, 17 (2) :14–20, 37. |
| [5] |
张德保, 沈鹏. 对海上目标毫米波 RCS 测量中的大气衰减修正方法[J]. 水雷战与舰船防护 , 2012, 20 (2) :26–28, 82.
ZHAND De-bao, SHEN Peng. The revision method of atmosphere attenuation to millimeter wave RCS measurement for sea target[J]. Mine Warfare & Ship Self-Defence , 2012, 20 (2) :26–28, 82. |
| [6] |
宋广, 李永新, 刘攀龙, 等. 海上毫米波大气衰减建模分析[J]. 水雷战与舰船防护 , 2011, 19 (2) :9–12.
SONG Guang, LI Yong-xin, LIU Pan-long, et al. Research on the model of millimeter-wave attenuation in atmosphere over sea[J]. Mine Warfare & Ship Self-Defence , 2011, 19 (2) :9–12. |
| [7] |
孙永侃, 康凤举, 熊正祥. 对毫米波制导反舰导弹实施质心干扰的仿真研究[J]. 系统仿真学报 , 2005, 17 (6) :1487–1489.
SUN Yong-kan, KANG Feng-ju, XIONG Zheng-xiang. Research on ship chaff centriod jamming against millimeter guided anti-ship missile simulation[J]. Journal of System Simulation , 2005, 17 (6) :1487–1489. |
| [8] |
孙卫东, 刘鼎臣. 毫米波雷达制导反舰导弹作战性能研究[J]. 战术导弹技术 , 2004 (5) :29–32.
SUN Wei-dong, LIU Ding-chen. Research on performance of millimeter wave radar homing anti-ship missile[J]. Tactical Missile Technology , 2004 (5) :29–32. |
 2016, Vol. 38
2016, Vol. 38
