1 舰船消磁线圈

钢制舰船在地球磁场的磁化作用下，会产生舰船磁场，其存在对舰船生命力构成严重威胁^[1]。舰船消磁即是利用消磁线圈、消磁电源与电流调整器等设备组成消磁系统，基于无磁滞磁化原理，在线圈中通以特定波形的消磁电流，打乱舰船铁磁物质的磁畴排序，使其分布各向均匀，从而达到消除舰船磁场的目的。消磁线圈电感是重要的物理参数。

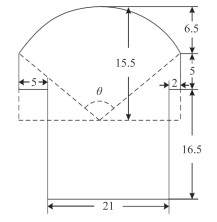
某消磁线圈轴向总长为 200 m，采用肋骨形式布设。从消磁区一端至另一端每隔 5 m 留有 1 道电缆槽，共 41 个槽，第 2 和第 40 道电缆槽各敷设 4 匝线圈，其余每槽敷设 2 匝，共计 86 匝。单匝线圈形状如图 1 所示（单位：m），图中 θ = 129.2°。

2 消磁线圈电感计算

线圈自感磁通链 ψ 与电流 i 的关系曲线即电感元件的韦安（Wb-A）特性，理想化的线性非时变电感元件磁通链 ψ 与电流 i 之比始终为正实常数，记作 L = ψ/i，称为元件的自感系数或电感系数，简称自感或电感。实际线圈电感的计算通常十分困难^[2-4]，对于形状很不规则的线圈尤其如此。

2.1 经验公式计算法

文献[5]提供了一系列电感计算公式。但对于复杂形状的线圈，仅有一些经验公式，且需先将线圈形状作近似规则化。将消磁线圈近似看成圆形螺线管，使单匝线圈周长与实际相等，其底面圆的直径取为 34 m。文献^[5]提供了如下经验公式：

$L=\frac{\pi }{4}{{\mu }_{0}}{{w}^{2}}\frac{{{d}^{2}}}{a}{{K}_{\alpha }},$

(1)

式中：μ₀ 为真空磁导率；w 为螺线管匝数；d 为螺线管直径；a 为螺线管长度；K_α 为随比值 α = a/d 变化的系数。根据实际参数，得 α = a/d = 200/34 ≈ 5.88，由文献[5]，查到 K_α = 0.939 143。从而由式（1）计算得到线圈电感值为：

$L=\frac{\pi }{4}\times {{\mu }_{0}}\times {{86}^{2}}\times \frac{{{34}^{2}}}{200}\times 0.939143\approx 30.85\text{mH}\circ $

(2)

2.2 基于 Matlab 编程计算法

用式（1）求解消磁线圈电感，因对其形状作了大幅简化，必然存在相当误差。借助计算机工具，可提高计算结果的准确性。

相对于电工学其他场合的各类线圈，消磁线圈的体积是巨大的，不论是其截面积还是其纵向长度的数值都过于庞大；而且线圈尺寸与其导线尺寸之比也非常大，这给其电感计算带来很大难度。若使用目前常用的电磁场计算软件 Ansoft 给消磁线圈建立模型，可采取有限元方法，利用公式 L = 2 Wm/I² 由磁场能量来计算线圈自感。然而通过多次建模试验发现，线缆尺寸远小于线圈尺寸，网格剖分量非常大，普通计算机无法完成，而且计算精度很不稳定，结果不可靠。

恒定电流产生的磁场不随时间变化，磁感应强度 $\mathop {B}\limits^{\rightharpoonup} $ 只是空间位置的函数。把电流看作许多微段电流连接而成，求出各微段电流在某点产生的磁感应强度，利用叠加原理即可算出整段电流在此点的磁感应强度。设载流导线电流为 I，导线横截面的线度略去不计，称该电流为线电流。在线电流上取长为 dl 的定向线元 $d\mathop l\limits^{\rightharpoonup}$，规定 dl 方向与电流方向相同，将 $Id\mathop l\limits^{\rightharpoonup}$ 称为电流元。依据毕奥-萨伐尔定律，$Id\mathop l\limits^{\rightharpoonup}$ 在与其距离为 r 的点 P 处产生的磁感应强度为：

$d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B}=\frac{{{\mu }_{0}}}{4\pi }\frac{Id\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {l}\times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}{{{r}^{3}}},$

(3)

式中，${{\mu _0}}$ 为真空磁导率，${{\mu }_{0}}=4\pi \times {{10}^{-7}}$。

穿过磁场中任一给定面的磁感线总数称为该面的磁通量 Φ，$\phi = \int_S {\mathop B\limits^{\rightharpoonup} \cdot {\rm d}\mathop S\limits^{\rightharpoonup}} $。由毕奥-萨伐尔定律，任意给定闭合回路在空间任一点产生的磁感应强度大小与回路电流成正比，即对于电感元件，有 Φ = LI。

因此，将舰船消磁线圈看作由许多个完全相同的单匝独立导线线圈排列而成，每个线圈通以相同大小方向的恒定电流，基于上述定律及公式，可利用 Matlab 软件编制程序计算出在线圈中通电 1 A 时其内部区域的磁通量及消磁线圈电感值。编程试验表明其计算结果比较稳定，可靠性好。

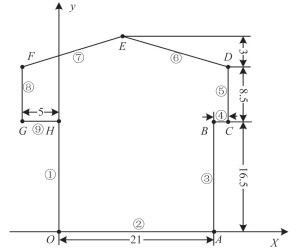
为了尽可能减小计算量，降低计算过程对计算机性能的过高要求，本着尽量不改变线圈截面积及周长，以减少计算结果与实际情况之间误差的思路，将单匝线圈的上半部分做一定简化以使其形状规则化。在此基础上建立二维坐标系，如图 2 所示。

图 2中各点坐标如下：O（0，0）；A（21，0）；B（21，16.5）；C（23，16.5）；D（23，25）；E（9，28）；F（-5，25）；G（-5，16.5）；H（0，16.5）。EF 所在直线方程为 $y = \frac{3}{{14}}(x + 5) + 25$，ED 所在直线方程 $y = - \frac{3}{{14}}(x - 23) + 25$。为了编写程序的方便，对图中线圈各段导线进行编号：HO 为第 1 段，OA 为第 2 段，AB 为第 3 段，BC 为第 4 段，CD 为第 5 段，DE 为第 6 段，EF 为第 7 段，FG 为第 8 段，GH 为第 9 段。

2.2.1 区域离散化

计算电感的关键在于计算穿过线圈截面的磁通量^[6-7]。利用 Matlab 编制电感计算程序如下。

[X,Y] = meshgrid（-4.999∶0.011∶23,28∶ -0.011∶0）；% 生成 2 维平面网格，

Z₁ =（Y <（3/14*（X + 5）+ 25））；% 第 7 段导体所在直线下方区域为逻辑 1，

Z₂ =（Y <（-3/14*（X - 23）+ 25））；% 第 6 段导体所在直线下方区域为逻辑 1，

Z₃ =（X > -4.984 9）；% 第 8 段导体所在直线右方区域为逻辑 1，

Z₄ =（X < 22.984 9）；% 第 5 段导体所在直线左方区域为逻辑 1，

Z₅ =（Y > 16.515 1）；% 线圈腰部上方区域为逻辑 1，

A₁ = Z₁ & Z₂ & Z₃ & Z₄ & Z₅；% 线圈内上半区域为逻辑 1，

Z₆ =（X > 0.015 138 8）；% 第 1 段导体所在直线右方区域为逻辑 1，

Z₇ =（X < 20.984 9）；% 第 3 段导体所在直线左方区域为逻辑 1，

Z₈ =（Y > 0.015 138 8）；% 第 2 段导体所在直线下方区域为逻辑 1，

Z₉ =（Y < 16.6）；% 线圈腰部下方区域为逻辑 1，

A₂ = Z₆ & Z₇ & Z₈ & Z₉；% 线圈内下半区域为逻辑 1，

Z=A₁|A₂；% 上下半区域组成完整的线圈内部区域，即计算有效区域。

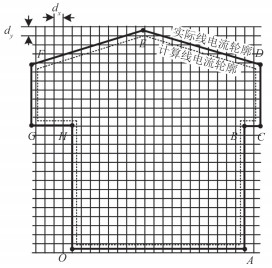
程序中变量 X，Y 为矩形区域所有网格节点在二维坐标系下的位置矩阵，Z 为线圈内部网格节点的索引号。图 3 为线圈截面的离散示意图。

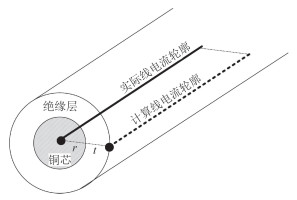
需要指出，线电流是理想化的模型，本文将实际的通电导线等效为线电流是为了方便利用现成的磁场解析公式，但线电流附近的磁场与距离成反比，当距离线电流无限近时，磁场趋于无穷大。在磁通区域离散化的过程中，必须避免这一点。计算线电流轮廓可根据实际电缆铜芯线规与绝缘层厚度确定。以圆导线为例，如图 4 所示，实际线电流轮廓与计算线电流轮廓之间的区域对线圈磁通没有贡献，其宽度为：

$d=r+t,$

(4)

另由线圈敷设形式可知，在 X-Y-Z 三维坐标系中，将第一个导线槽为起点，则第 i 个导线槽的 Z 坐标为：

$Z=5(i-1)\circ $

(5)

2.2.2 磁链计算

本文的消磁线圈沿轴向分布在 41 个导线槽内，彼此相互串联。计算磁链时，为了计算方便且不改变其物理本质，可等效为 41 组通有相同电流的独立线圈。不考虑电感非线性，则消磁线圈电感与电流无关，以下分析假设线圈电流为 1 A。

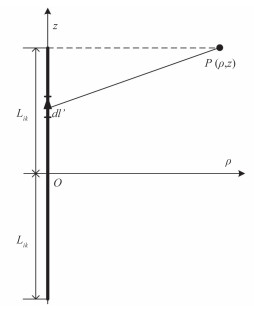
设第 i 个导线槽内匝数为 N_i，其中第 k 段（k = 1，2，…，8，9）导体长度为 2 L_ik，由电磁场理论可知，第 k 段导线在导线外任意点 P 产生的磁感应强度为：

$\begin{align} & \underset{ik}{\mathop{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B}}}}\,(\rho ,z)= \\ & \underset{\phi }{\mathop{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}}}}\,\frac{{{\mu }_{0}}{{N}_{i}}}{4\pi \rho }\left[ \frac{z+{{L}_{ik}}}{\sqrt{{{\rho }^{2}}+{{(z+{{L}_{ik}})}^{2}}}}-\frac{z-{{L}_{ik}}}{\sqrt{{{\rho }^{2}}+{{(z-{{L}_{ik}})}^{2}}}} \right]\circ \\ \end{align}$

(6)

式中：$\underset{\phi }{\mathop{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}}}}\,$ 为单位矢量；ρ 和 z 为空间某点在以导线段中心为坐标原点的局部坐标系中的坐标，如图 5 所示。

第 i 槽线圈在空间产生的磁密为 9 段导体产生的磁密合成：

$\underset{i}{\mathop{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B}}}}\,(\rho ,z)=\sum\limits_{k=1}^{9}{\underset{ik}{\mathop{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B}}}}\,(\rho ,z)},$

(7)

设第 j 槽线圈匝数为 N_j（i，j = 1，2，3…41），则第 i 槽线圈通 1 A 电流时在第 j 槽线圈产生的磁链为：

${{\phi }_{ij}}=\underset{i}{\mathop{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B}}}}\,({{\rho }_{j}},{{z}_{j}})\cdot \underset{j}{\mathop{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {S}}}}\,{{N}_{j}},$

(8)

式中 ${\mathop S\limits^{\rightharpoonup}_j}$ 为第 j 个槽线圈平面的法向矢量，其幅值大小为线圈面积。线圈电流设定为 1 A，那么所有槽线圈电感等于所有线圈磁链之和：

$L=\psi =\sum\limits_{i=1}^{41}{\sum\limits_{j=1}^{41}{{{\phi }_{ij}}}}\circ $

(9)

求解过程中分别取不同的计算步长，会使得结果有少许出入，但相差很小，多次计算的结果稳定在 0.045 H 附近。

与前面用经验公式计算所得的线圈电感值 30.85 mH 相比较，二者之间大约相差 30%。事实上，由于不规则线圈的电感计算的复杂性，经验公式必然比编程计算粗略许多，所以本文消磁线圈电感值应以 Matlab 程序计算结果为准，可取为 45 mH。

3 结语

舰船消磁线圈属于异型线圈，采用经验公式计算其电感值误差较大；而有限元方法虽精度高，但在计算大尺寸空心线圈时空间离散量过于庞大，普通微机根本无法实现。为了解决上述问题，本文基于 Biot-Savart 原理，将线圈区域离散化处理，提出了消磁线圈电感的数值计算方法。该方法为电感计算提供了新思路，且方便转化为计算机程序，推广到其他异型线圈的电感计算。