在数字采集系统中,一方面希望信号采样时用尽可能高的采样率;另一方面在信号处理时又希望尽可能降低信号速率,以降低对信号处理器件的性能要求[1]。这两者看似矛盾的需求,在数字下变频技术的支持下,成为一个有机整体。在水声声呐系统的接收机中,也正不断借鉴其技术,对水声信号的数字下变频技术实现有实际应用价值。
1 基本原理数字变频的概念是指把信号搬移到更高或者更低的载频上,可通过信号x(t)与1个旋转向量相乘得到,即$y(t)=x(t){e^{j2{\rm{\pi}}{f_c}t}}$,其中fc为载波频率。把基带信号搬移到该频点上就是上变频,将该信号从该频点搬移到基带则称为下变频。
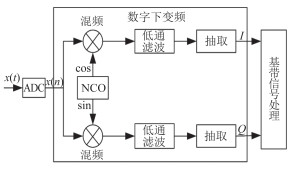
1.1 数字下变频数字下变频器(DDC)主要由数控振荡器(NCO)、混频器、低通滤波器及抽取器等组成[2-3]。DDC的核心部分是将A/D采样得到的信号与DDC中的数控振荡器(NCO)产生的本振信号混频,进行频谱搬移,得到零中频的基带复信号,分别为同相分量和正交分量。经过数字混频之后,此时信号的采样率仍然是ADC采样频率,数据率可能较高,信号的带宽远小于采样频率,所以需要经过低通抽取滤波器降低信号采样率,完成了下变频的过程。DDC的原理如图 1所示。
|
图 1 DDC的原理框图 Fig. 1 Schematic diagram of DDC |
数字控制振荡器(NCO)是产生一个给定频率信号的信号发生器,更确切的说是产生一个频率可变的正弦或余弦样本。
| $s(n) = \sin (2\pi {f_0} \cdot /{f_s}),(n = 0,1,2, \cdot \cdot \cdot )。$ |
其中
产生正弦或余弦信号样本最直接、最简便的方法是查表法[4],即事先根据正弦或余弦波的各个相位计算好相应的值,并按相位角度作为地址存储各相位的正、余弦样本值。
DDC以
数字混频器是将原始采样信号与本振信号正、余弦量分别相乘,最终得到正交的信号[5]。自然界中物理可实现的信号都是实信号,其频谱具有共轭对称性。因此,对于一个实信号,只需正频或者负频部分就能完全加于描述。对于一个实的窄带信号:
| $x(t)=a(t)\cos[{\omega_0}t+\phi(t)]。$ |
其解析信号可表示为:
| $s(t)=a(t){e^{j\phi(t)}}{e^{j{\omega_0}t}}。$ |
其中
| $\begin{array}{l} z(t)=s(t)\cdot{e^{-j{w_0}t}}=a(t)\cdot{e^{j\phi(t)}}=\\ a(t)(\cos\phi(t)+j\sin\phi(t))=I(t)+jQ(t)。 \end{array}$ |
基带信号为解析信号的复包络,是复信号,既有正频分量又有复频分量。在数字信号处理中,常常采用数字混频正交变换来进行数字信号的正交分解,即将原始信号
在数字下变频器中,关键的问题是数据抽取后的数字滤波。对于基带数据抽取,数字滤波器为低通滤波。数字滤波器的输入为
| $y(n)=\sum\limits_{k=-\infty}^\infty{h(k)\cdot(n-k)},$ |
数字滤波器可以用,有限冲激响应(FIR)和无限冲击响应(IIR)滤波器2种形式[6]。FIR滤波器是指冲激响应
| $H({e^{j\omega }}) = \sum\limits_{k = 0}^{N - 1} {h(k) \cdot {e^{ - j\omega k}}}。 $ |
相比于IIR滤波器,FIR滤波器具有线性相位、稳定性等特点,适于声呐中信号处理的要求,并且其设计相对成熟。常用的设计方法有窗函数设计法、频率采样设计法和等同纹波设计法等,其中窗函数设计法是最简单,也是最常用的设计方法。该方法是用一个FIR滤波器的频率响应来逼近所要求的理想滤波器的频率响应:
| $h(n) = \frac{1}{{2\pi }}\int_{ - \pi }^\pi {H({e^{j\omega }}){e^{j\omega n}}} {\rm{d}}\omega 。$ |
窗函数法就是选择已知的窗函数
常见的窗函数有矩形窗、三角窗、汉宁窗、布拉克曼和凯塞窗函数等。
1.5 多速率信号抽取在完成信号的基带搬移后,还需要降低数据率,以满足基带信号处理的要求,此为多速率信号处理过程要解决的问题。其最基本2个过程为抽取和内插,抽取就是降低数据率而内插为提高数据率[7]。
整数倍的抽取是指把原始采样序列
| $x(m)=x(mN)。$ |
如果序列
上述各功能模块级联起来,形成一个下变频系统。在水声声呐系统中,信号频率较软件无线电中低很多,其高频声呐也只有千赫兹级,信号形式多为线性调频、单频等信号。
下变频中主要包括部分:混频和滤波。将输入信号与NCO产生的本振信号做乘法运算,输出运算结果,构成混频部分。而滤波部分是为滤除杂散的频率成分,得到预期信号。
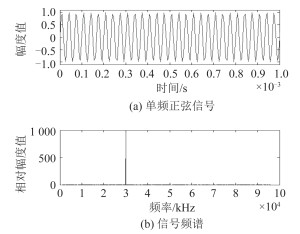
2.1 NCO产生和混频器当输入信号为单频信号
|
图 2 频率为30 kHz的正弦信号时频图 Fig. 2 30 kHz Sine signal in time and frequency domain |
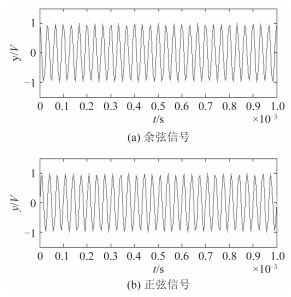
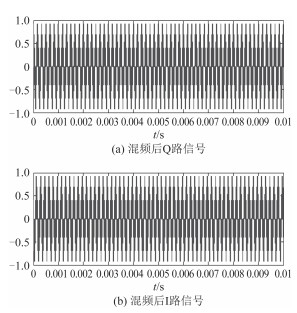
NCO本振信号频率为24kHz,采样率为192kHz,产生正交的正、余弦分量,与输入信号混频,进行频谱搬移。图 3为正余弦分量信号时域波形,截取一定时间。图 4为混频后的输出信号。
|
图 3 本振信号24 kHz Fig. 3 24 kHz Sine and cosine signal |
|
图 4 混频后的I、Q时域信号 Fig. 4 I and Q singal after frequency mixing |
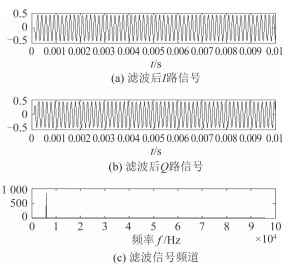
以汉宁窗函数作为FIR滤波器的滑动窗口,n=50阶,混频后的数据通过FIR滤波器,得到的波形如5图所示,可以看出其I和Q路信号的时域波形,并且分析得到频谱,符合理论计算。
|
图 5 FIR滤波后的时频图 Fig. 5 I and Q signal in time and frequency domain after FIR filter |
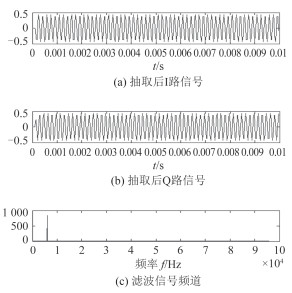
经数字FIR滤波滤除杂散频率,进一步以6:1抽取数据,以降低数据率,原采样率为192kHz,抽取后为32kHz。在Matlab中,以该比例抽取数据,重组数据得到新的数据序列,如图 6所示,可以看出其I和Q路信号的时域波形,采样率明显降低,但其频谱成分不会改变。
|
图 6 数据抽取的时频信号图 Fig. 6 I and Q signal in time and frequency domain after data decimation |
FPGA芯片选择为Altera公司的CycloneIII的EP3C120型号,芯片内部具有119k的LE单元,288个18bit×18bit的乘法器,片内RAM有3.88kbits,系统的主时钟为50MHz,应用Verilog语言编程+IP核的设计的设计方法。
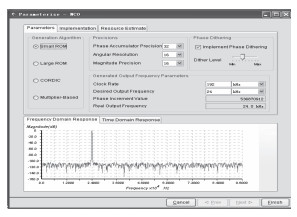
3.1 NCO模块的实现NCO主要产生正交的正余弦分量,其实质是实现频率的合成,而直接数字频率合成(DDS)技术是一种全新的频率合成技术,具有频率分辨率高、转换速度快和相位连续等特点。在EP3C120的IP核库中,具有DDS模块,可以配置参数生成特定的输出信号。其模块如图 7所示。
|
图 7 DDS的配置参数示意图 Fig. 7 DDS configuration diagram |
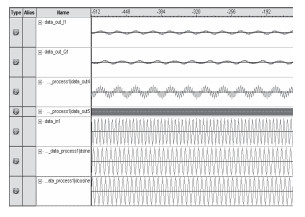
其中clk为输入时钟192kHz,phi_inc_i为参数值,决定输出信号的频率,字长为16bit。图 8中dsine和dcosine是在signaltapII中DDS的输出信号本振信号。
|
图 8 Signaltap中DDS输出信号 Fig. 8 DDS outputs in signaltap II |
混频的实质是将中频信号的采样值与本振信号进行乘法运算,因此混频器可用乘法器代替。在EP3C120中,内部有一定的乘法器资源,在Quartus编程设计时例化乘法器宏模块。
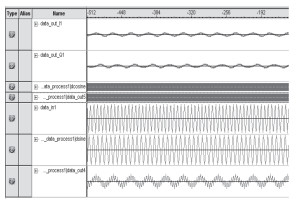
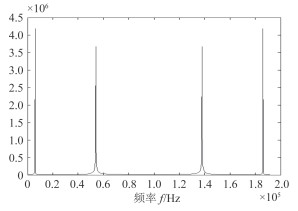
设data_in1为输入信号30kHz,作为乘法器的输入变量,dsine为24kHz的本振正弦信号,作为乘法器的另一变量。在FPGA内部嵌入式逻辑分析仪signaltap中,各变量如图 9所示,其中的data_out4即为乘法器的输出结果,把相应的变量值保存为tbl数据格式,导入Matlab中,分析其混频后变量data_out4的频谱,如图 10所示。
|
图 9 混频后的signaltap中的信号量 Fig. 9 Signals in signaltap after multiplication |
|
图 10 混频后的频谱图 Fig. 10 The frequency spectrum after multiplication |
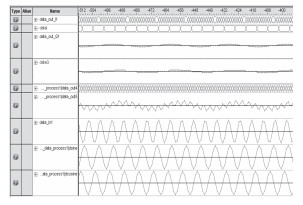
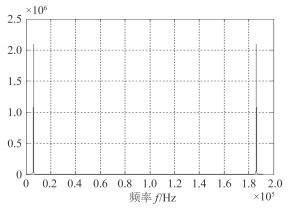
在混频器完成频带的搬移之后,从频谱图 13可看出存在着其他频率成分。Cyclone系列FPGA支持FIRII型滤波器IP核,设置低通滤波为50阶,选择Hanning窗函数,截止频率为7kHz。图 11是经过FIP滤波和数据抽取后相关信号量的示意图,其中dataI和dataQ是滤波器的输出。图 12是经滤波后的信号频谱示意图,比较图 10和图 12,能很好地滤除带外的分量。
|
图 11 滤波及数据抽取后的信号量 Fig. 11 Signals in signaltap after filter and decimation |
|
图 12 滤波后的信号频谱图 Fig. 12 The frequency spectrum after filter |
|
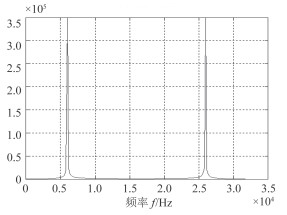
图 13 数据抽取后的频谱图 Fig. 13 The frequency spectrum after data decimation |
设计数据抽取器,以6:1的系数抽取,原始数据采样率为192kHz,抽取后数据率为32kHz,基带信号为6kHz,仍满足采样定理。在FPGA中,将数据信号进行同步时钟的6分频,然后利用该时钟去采样得到的新序列数据即为抽取后的信号。如图 11所示,其中data_out_I1和data_out_Q1为抽取前数据,dataI和dataQ为抽取后正交、同相分量。可以看出其波形的正确性。在Matlab中频谱分析如图 13所示,分析其频谱为6kHz,与理论上的数字下变频仿真一致。
4 结 语水声信号数字下变频的实现,实现了信号的基带频谱搬移、系统处理数据率的降低,因此大大降低了对信号处理机处理能力的要求。本文所设计的模块已经应用到某水声声纳设备的前置预处理分机中,假设原始信号频率为30kHz,采样率为192kHz,数据16位,50个通道,则数据率为16bit×50×192kHz=150Mb/s,下变频后的基带信号频率为6kHz,采样率为32kHz,则数据率为16bit×50×32kHz=25Mb/s,经整机联调测试,以及湖试等验证功能的正确性。
| [1] | 曹李秋.软件无线电数字下变频FPGA实现的研究[D].武汉:武汉理工大学, 2006. http://cdmd.cnki.com.cn/article/cdmd-10497-2006061306.htm |
| [2] | 高亚军. 基于FPGA的数字信号处理[M]. 北京: 电子工业出版社, 2012 : 121 -130. |
| [3] | 陈东坡.数字下变频电路的FPGA实现[D].西安:西安电子科技大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10701-2009195642.htm |
| [4] | 周俊峰, 陈涛. 基于FPGA的直接数字频率合成器的设计和实现[J]. 电子技术应用 , 2002, 28 (8) :34–36. |
| [5] | 胡跃, 张正鸿. 基于FPGA的数字正交混频变换算法的实现[J]. 国外电子测量技术 , 2007, 26 (5) :9–11. |
| [6] | 奥本海默A V, 谢费R W, 巴克J R.离散时间信号处理[M].刘树棠, 黄建国, 译.西安:西安交通大学出版社, 2007: 352-412. |
| [7] | 西瑞克斯(北京)通信设备有限公司. 无线通信的MATLAB和FPGA实现[M]. 北京: 人民邮电出版社, 2009 : 90 -97. |
| [8] | 胡广书. 数字信号处理理论、算法与实现第3版[M]. 北京: 清华大学, 2012 : 355 -363. |
 2016, Vol. 38
2016, Vol. 38
