一般来说大型船舶的机舱等舱室内部空间有限,使得系统管路没有足够的空间布置,系统管路走向会直接影响设备的进流状况,进而会导致设备的振动加剧[1-2],长期如此会缩短设备的使用寿命。限于舱室的空间大小,通过增加水泵进口直管段的长度,以及增大水泵进口弯头半径来优化进流状态是不现实的。
针对水泵进口流场恶化导致的振动加剧问题,通常有优化进口流道和添加流场均匀设备等办法。有很多文献对泵站的进口流道造型曲线[3]开展了研究,合理的型线设计可以提高水泵进口流场的均匀度,防止水泵发生气蚀。有部分研究在弯头内部转弯半径方向添加导流叶片[4],用于引导流体通过弯头时的流场,减弱漩涡区域范围和强度,抑制脱落涡的生成。
对于流场均匀性的评价,相关的研究主要集中在水洞和风洞设计上,对于流场品质的考察主要体现在流速不均匀度、流场平均速度角、压力不均匀度等方面[3-5]。陆林广[6-9]在研究水泵进口流道造型时,提出了进口流道优化设计的目标函数,主要包括流速分布均匀度和水流入泵平均角度。我国航空领域对于对风洞的品质有更为严格的要求,GJB 1179A-2012《低速风洞和高速风洞流场品质要求》[10]中明确规定了高低速风洞的湍流度[11]、轴向静压梯度、动压稳定性等性能参数值范围。
本文选取水泵进口段弯头流场作为研究对象,设计了3种流场均匀装置安装于水泵进口管段,分别对其开展数值仿真计算和试验研究,获取不同流场均匀装置的流阻系统、速度场、方向场的分布,并对安装不同流场均匀装置后水泵的振动及噪声进行分析。
1 流场均匀装置模型本文的主要研究对象为安装在水泵进口位置管道内的流场均匀装置,其工作介质为水,主要用于改善泵入口流场,进而降低泵的振动及辐射噪声。流场均匀装置的初始设计方案分别对应矩形格栅、导流锥体、同心圆3种方案,长度分别为0.5、1倍的管道通径d。
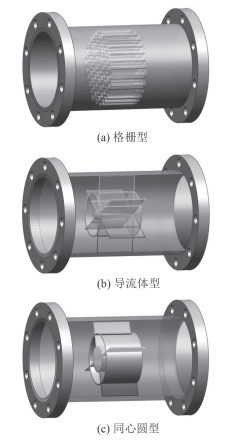
|
图 1 流场均匀装置 Fig. 1 The rectifer of flow field |
为了真实模拟水流通过水泵前弯头的流场紊乱状况,按照实际水泵管路布置进行建模,计算管道模型三维布置如图 2所示。本文重点关注水泵进口流场的均匀效果,只针对进口管路装置进行数值模拟,不考虑阀门开启状态。其中泵进口弯头半径为1D,进口远端弯头半径为2D,在均匀装置出口位置段上即水泵进口位置处设置监控点M、出口评价平面S2和进口评价平面S1,平面S1和S2离进出口距离均为0.5 m。

|
图 2 数值计算模型及网格 Fig. 2 The geometry of the rectifer and the gird |
为了降低不同的网格结构尺度对数值计算结果的影响,对管道模型不同段进行分区处理,将数值计算模型划分如图 2所示,其中A、C部分为圆管段,采用结构化网格;B区为流场均匀化装置段,考虑到均匀化装置格栅的微小结构,采用非结构化网格进行计算,在其壁面添加附面层进行加密。在进行不同均匀化装置及不同阀门开度模型计算时,只需更换B区网格,所有模型数值计算时采用相同的拓扑结构和网格,网格量统计如表 1所示。
|
|
表 1 不同均匀化装置模型对应的网格量 Tab.1 The grids number of the different rectfiers |
采用Fluent商用软件作为数值计算求解器,利用interface作为不同块之间的交界面进行数据传递和处理。进口边界条件给定为流量,进口速度方向给定为normal to boundary,软件根据实际计算情况自动调节进口速度方向;出口给定大气压。采用标准k-ε两方程湍流模型和SIMPLE算法,近壁面处理采用标准的壁面函数,其他给定为壁面边界条件。压力采用二阶离散,动量方程、k方程、ε方程均采用二阶迎风格式进行离散,保证计算精度。详细的数值模拟工况如表 2所示,对应水泵不同的转速工况,共6 × 7=42组计算文件。
|
|
表 2 数值模拟工况表 Tab.2 The conditions of numerical simulation |
在数值计算中分别对出口平面的面积加权平均速度进行了监控,同时对出口段内点M的压力和速度进行了监控。以直管,流量为250 t/h为基础算例,它的Fluent数值计算残差收敛曲线以及M点压力速度监控曲线如图 3所示。通过残差收敛曲线以及监控点的压力速度曲线可以得到,在数值计算进行到1 500步以后各分量残差以及监控点的压力速度均保持不变,监控点的表压保持在89.5 Pa,速度保持在2.17 m/s,视为数值计算结果收敛,其它算例保持相同的设置,收敛情况相同。

|
图 3 数值计算收敛曲线 Fig. 3 The convergence curves of numerical simulation |
将流场均匀化装置安装在管道中,会增加流道的阻力。评价均匀化装置的水力性能用阻力系数λ来表示,其定义如下式:
| ${\rm{ }}\lambda {\rm{ }} = \frac{{2\Delta {p_j}}}{{{\rm{ }}\rho {\rm{ }}{{\bar U}^2}}},$ | (1) |
| $\Delta {p_j} = \Delta {p_t} - \Delta {p_g}$ | (2) |
式中:ΔPt,ΔPg,ΔPi分别为计算模型总压差、管路总压差,及均匀流装置总压差;0.5 pU2为通道截面平均动压。在模型计算阻力系数时选取S1、S2截面做对比参考,并减去相同流量下直管的管道阻力损失,即为流场均匀装置的流阻,参考式(2)。
图 4给出了不同流场均匀装置阻力系数与流量的关系图。可以看出,随着流量的增加(流速的增大),均匀装置的阻力系数逐渐降低。同心圆0.5D的阻力系数在所有工况下最小,网格1D最大。计算流场均匀装置各工况下平均阻力系数,同心圆0.5D的阻力系数约为网格1D阻力系数的13%。流场均匀装置流阻系数由大到小排序为:网格1D > 网格0.5D > 导流体1D > 同心圆1D > 导流体0.5D > 同心圆0.5D。流场均匀装置网格0.5D和网格1D的阻力系数至少为其它流场均匀装置的3.4倍。
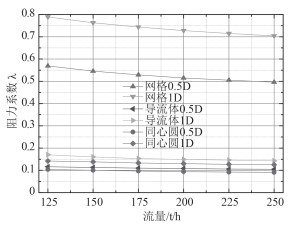
|
图 4 流场均匀装置阻力系数与流量关系图 Fig. 4 The relationship between the flow rate with the resistance coefficent for different rectfiers |
参考水洞、风洞等文献及标准对流场品质的要求,本文主要选取速度场、压力场进行流场均匀性分析,分别对应轴向速度不均匀度、平均轴向速度角、压力不均匀度。
1)轴向速度不均匀度
定义轴向速度不均匀系数
| ${\rm{ }}\xi {{\rm{ }}_u} = \frac{1}{{\rm{Q}}}\int {\sqrt {{{\left( {u - \bar U} \right)}^2}} {\rm{d}}A} 。$ | (3) |
式中:Q为截面流量;u为截面上各网格单元dA上的轴向速度;$\bar U$为截面的平均速度,ξu为截面的速度不均匀系数。
图 5给出了S1和S2截面的轴向速度不均匀系数与流量关系,通过对比分析可知:1)所有的流场均匀装置几乎具有相同的进口轴向速度分布;2)出口截面S2流场不均匀系数排序分别为导流体1D > 导流体0.5D > 同心圆1D > 同心圆0.5D > 网格0.5D > 网格1D > 直管。

|
图 5 均匀装置的轴向速度不均匀系数与流量关系 Fig. 5 The relationship between the flow rate with the uniformity of the axial velocity for different rectfiers |
图 6选出部分流场均匀装置进出口速度分布云图,对应泵的流量为250 t/h。选取截面分别位于距离流场均匀装置进口0.5D,距离均匀装置出口0.5D,1D,1.5D,2D,2.5D。在没有布置流场均匀装置的情况下,靠近弯头内壁出的速度较小,靠近弯头外侧的速度较大,形成了流场高低速分布的差异性,经过3倍通径长度的直管段整流,截面的流速分布均匀性仍然较差。
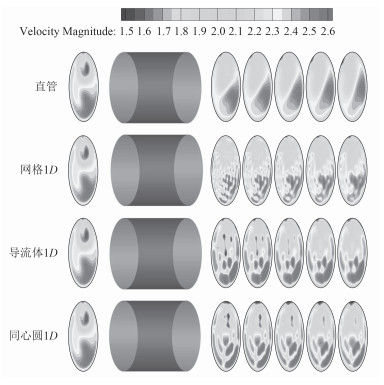
|
图 6 均匀装置进出口的速度分布云图 Fig. 6 The colormap of velocity at the inlet and outlet of rectfiers |
在添加了流场均匀装置以后,对于流场均匀装置进口速度分布几乎没有影响,主要的差异体现在经过流场均匀装置以后速度场的分布。
对于网格式的流场均匀装置,其将流道划分为多个蜂窝型的狭长流道,最大程度上破坏了原有涡系结构,经过狭长流道的整流作用,在到达流道出口位置时内部整流已经初步达到均匀。在出口位置由于流道截面积的增加,不同细小流道之间的流场二次混合,且出口流速较高;后经过直管段的整流作用,不同网格流道间的差异性逐渐减小。
导流体1D分别从周向和径向将流道划分为几个区间,流体在进入均匀装置以后,轴向上流道由窄逐渐变宽,在流出均匀装置的过程中流动损失要小于网格1D,出口流场经过直管段的整流后,原有速度场在径向上的分布要优于网格1D。
流场均匀装置同心圆1D在径向上划分为2部分,均匀装置的中心部分为圆柱,流体通过同心圆1D以后在径向上明显被划分为3部分,且3部分通过3倍通径长度的直管段整流后分层现象仍然明显,尤其是对于低流速分布的整流效果较差。
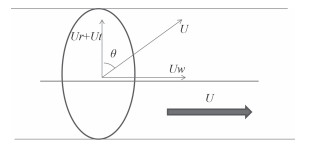
|
图 7 轴向速度角定义 Fig. 7 The definition of the axial velocity angle |
2)轴向速度角分析
对截面轴向速度角以及截面平均速度角定义如下:
| $\theta = \arctan (Uw/(Ur + Ut)),$ | (4) |
| $bar\theta = \sum\limits_{i = 1}^n {{\theta _i}{A_i}} /\sum\limits_{i = 1}^n {{A_i}}。 $ | (5) |
式中:Ai为截面单元微元面积;θi为截面上各网格单元dA上的轴向速度,$\bar \theta $为截面的平均速度角。
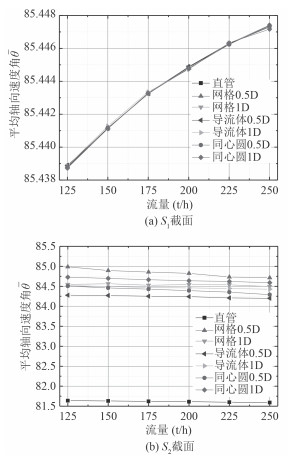
图 8给出了轴向速度角与流量的关系图。对比不同状态下均匀装置的轴向速度角分布可以得出:
|
图 8 均匀装置的轴向速度角度与流量关系 Fig. 8 The relaiton between the axial velocity angle with the flow coefficent |
1)安装不同的流场均匀装置后,进口S1平面的轴向速度角几乎保持不变,且随着流速的增加,平均速度角微弱增加;
2)随着流量/流速的增加,流场均匀装置后的S2截面平均轴向速度角微降;对比直管段,流场均匀装置都能够明显的改善流体轴向速度角,各流场均匀装置间差距较小,最大相差只有0.8°,水流经流场均匀装置整流以后至少提高了2.5°,流场均匀能够显著提高平均速度角;
3)轴向速度角总体变化规律为:网格0.5D > 同心圆1D > 网格1D > 导流体1D > 同心圆0.5D > 导流体0.5D > 直管。
3)压力场不均匀度分析
定义截面压力不均匀系数为:
| ${\rm{ }}\xi {{\rm{ }}_p} = \frac{1}{{\bar PS}}\int {\sqrt {{{\left( {p - \bar P} \right)}^2}} {\rm{d}}A} 。$ | (6) |
式中:S为截面面积;p为截面上各网格单元dA上的平均压力; $\bar p$为截面的平均压力。
图 9给出了流量与S1及S2截面压力不均匀系数与流量的关系。通过对比可知:

|
图 9 均匀装置的压力不均匀系数与流量关系 Fig. 9 The relaiton between the pressure uniformity with the flow coefficent |
1)对于所有的流量工况,S1截面的压力不均匀度都小于1‰,不同流场均匀装置的进口状态相同,差异极小;
2)随着流量的增加(流速增加),S2截面的流场不均匀系数逐渐加大;
3)当不添加流场均匀装置时,其直管段S2截面的流场不均匀系数最大,所有的流场均匀装置都能够有效提高压力均匀分布;
4)对比不同均匀装置S2的,流场均匀装置的压力均匀效果排序为:网格0.5D > 网格1D > 同心圆1D > 同心圆0.5D > 导流体1D > 导流体0.5D > 直管。
3 试验测试及结果分析本文选取大型船舶的水泵附近管路作为研究对象,搭建试验台架,通过变化进口阀门开度获得不同均匀性的进口流场,用于测试流场均匀装置在不同进流条件下的均匀效果,选取水泵出口端叶频线谱值作为最终评价参数。
3.1试验台架组成
流场均匀装置的试验台架如图 10所示,主要由水泵、截止止回阀、进口阀、测试段、流场均匀装置、进口弯头组成;其中流场均匀装置安装于水泵进口位置,测试管段位于水泵出口下游,通过调整进口阀开度实现对进流条件的控制。测试针对不同流场均匀装置,分别对应水泵转速1(高转速)、转速2(低转速)两个转速状态,对应进口阀90,60,30°三个开度状态。
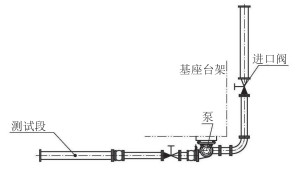
|
图 10 流场均匀装置测试布置图 Fig. 10 The test rig of the rectfier |
试验为流场均匀装置测试,每次测试时分别测试3个进口阀门开度。固定泵进口弯头为1D弯头,保持其他管路安装状态不变,更换流场均匀装置进行测试。测试工况如表 3所示。
|
|
表 3 流场均匀装置测试工况表 Tab.3 The condition of experiments |
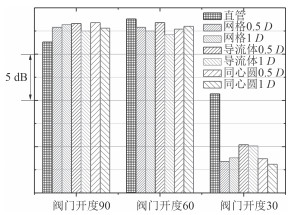
图 11给出了泵在转速1时,测试段对应的不同流场均匀装置流噪声测试结果。由图可知:
|
图 11 泵转速叶频值分布直方图(转速1) Fig. 11 The BPF noise of the pump(No. 1) |
1)在进口阀门开度为90°状态下,此时泵的进流状态较好,直管对应的叶频线谱均小于其它流场均匀装置。导流体0.5D和同心圆0.5D叶频线谱值最大,比直管高约2.1 dB;导流体1D对比于直管,增加值约为1.2 dB,同心圆1D增加为1.5 dB;
2)当进口阀门开度为60°时,此时泵的进流状态相比于阀门开度为90°出现了一定恶化,测试得到的直管对应叶频线谱值最高,所有的流场均匀装置对降低叶频线谱都开始体现出一定的效果;其中导流体1D的叶频线谱最小效果最佳,比直管段减低了1.9 dB;网格1D降低了1.3 dB;
3)当进口阀开度为30°时,此时泵的进流状态急剧恶化,所有流场均匀装置都有较好的降噪效果,至少有5 dB的降噪效果,其中同心圆1D的降低效果最明显,达到了7.6 dB。
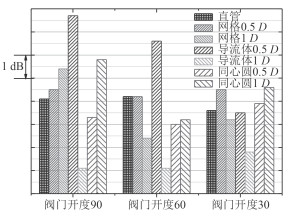
图 12给出了泵在转速2时,测试段对应的不同流场均匀装置流噪声测试结果。由图可知:
|
图 12 泵转速叶频值分布直方图(转速2) Fig. 12 The BPF noise of the pump(No. 2) |
1)当进口阀开度为90°时,此时泵的进流状态较好,导流体1D降低泵叶频线谱值最佳,达到了3 dB;同心圆0.5D也有0.8 dB的叶频降低效果;其他的流场均匀装置的叶频线谱值均大于直管段;
2)当进口阀开度为60°时,此时泵的进流状态相比于阀门开度90°出现一定的恶化,网格1D和导流体1D显示出了比较明显的降噪效果,其中在进口阀60°时分别降低约1.8 dB和3.1 dB;
3)当进口阀开度为30°时,导流体1D的降低效果最明显,约为1.8 dB。
纵向对比图 11和图 12水泵在相同进口阀门开度、不同转速下对应的出口叶频线谱可以得出:
1)流场均匀装置的叶频降低效果与流速、泵进流状态密切相关;
2)当泵转速较高、进流状态较好时,流场均匀装置并不能够很好的降低泵出口叶频线谱;
3)当泵进流状态恶化时(进口阀门开度30°),流场均匀装置能够有效的降低叶频线谱值。
综上分析可以得出:
1)当泵转速较高进流状态较好时,流场均匀装置会小幅度的增加泵出口叶频线谱;当进流状态开始恶化时,流场均匀装置开始显示一定的降噪效果;当进流状态大幅度恶化,流场均匀装置可以大幅降低泵叶频线谱,最低的降噪效果有5.5 dB。
2)当泵转速较低时,在不同的阀门开度小,部分流场均匀装置能够有效的降低泵出口叶频线谱,其中导流体1D能够适应不同的泵进流状态,在所有的阀门开度下都有较大的降低效果。
4 结语本文对不同流场均匀装置对降低水泵出口叶频效果开展了研究,对针对3型6个流场均匀装置进行了详细数值计算,通过对比出口叶频水声线谱及流场均匀性评估参数,结论如下:
1)网格1D和网格0.5D均流装置的流阻系数至少是设计方案的3倍,远大于其它均流装置。进口截面轴向平均速度角是影响水泵进流状态最关键的参数,在不考虑网格0.5D和网格1D的情况下,同心圆1D、导流体1D、同心圆0.5D、导流体0.5D都具有相当的一定流场均匀效果。根据压力不均匀度和轴系速度不均匀度分布可知,各流场均匀装置与直管之间差异极小,这2个参数对泵进进流状态影响有限。
2)导流体1D对比直管以及其他流场均匀装置,能够适应较宽水泵转速及进流状态。泵在高转速运转时,进口阀门开度为30°时导流体1D降噪效果能够达到5.7 dB;当进流状态较好且泵位于高转速时,进口阀开度为90°时,虽然没能够降低叶频线谱,但其使得增加值只有1.2 dB,具有较广的使用范围。
 2016, Vol. 38
2016, Vol. 38
