为了达到安全航行及节省能源的目的,需要设计出有效的控制器使船舶按照期望的航线航行。但由于船舶是典型的欠驱动系统,缺少横向推动装置,因此仅仅依靠基于向量的控制方法难以有效解决欠驱动船舶的航迹跟踪控制问题[1]。同时,考虑到船舶的非线性、大时滞、大惯性等特点,很难设计出完全基于精确数学模型的控制器,因此,有必要进一步对船舶航迹跟踪控制进行探索和研究。
目前,国内外学者对船舶运动控制进行了大量的研究。文献[2]将重定义输出和Backstepping方法引入控制器,提出全局k指数稳定及状态反馈航迹直线跟踪控制律,但忽略了横漂对船舶运动造成的影响,难以实现曲线跟踪控制;文献[3]和采用2个级联子系统构造出船舶航迹误差跟踪系统,通过Backstepping技术和Lyapunov方法对变换后的系统设计出船舶航迹跟踪控制律,但它是基于精确数学模型设计的控制器,局限性大,调参难度较大;文献[4-5]设计的船舶航迹跟踪自适应控制律对模型参数不确定及外界干扰具有较强的鲁棒性,但由于调参个数较多,计算复杂,难于工程实现;文献[6]采用反馈线性化方法建立模型等价式,将其解耦为2个线性系统,设计出动态反馈控制律,确保跟踪误差稳定,实现了存在干扰下的船舶航迹跟踪控制;文献[7]将非线性滑模迭代和增量反馈结合,设计出可应用与船舶直线和曲线控制的非线性反馈控制律,克服了对精确数学模型的依赖,但多次对函数求微分增大了计算量,给工程应用带来很大阻碍。
本文利用自抗扰控制器(ADRC)中的扩张状态观测器(ESO)模块对船舶内部不确定扰动和外界干扰进行实时估计,使得系统不需要依赖于精确的船舶数学模型;将快速终端滑模(FTSM)切换面引入非线性状态反馈(NLSEF)中,结合幂指数趋近律,设计出快速终端滑模自抗扰(FTSM-ADRC)控制律,在保证自抗扰控制器优点的前提下提高系统状态的收敛速度,改善系统抖振,减少可调参数,易于工程实现。
1 船舶运动数学模型考虑受到恒定风、浪和流的外界干扰,以及舵机特性的欠驱动水面船舶的运动数学模型如下:
| $ \left\{ \begin{gathered} \dot x = u\cos \varphi -v\sin \varphi\text{,} \\ \dot y = u\sin \varphi + v\cos \varphi\text{,} \\ \dot \varphi = r \text{,} \\ \dot r = f(r) + \omega (t) + b\delta\text{。} \\ \end{gathered} \right. $ | (1) |
式中:x,y分别为以大地坐标系为参考的船舶纵向位置和横向位置;u,v分别为船舶对地前进速度和横向速度;φ,r分别为船舶的船首向和转首速率;f(r)为船舶内部转首速率造成的扰动,取
本文将船舶模型与舵机系统组成串联系统,船舶考虑舵机特性,可用以下方程表示:
| $ \dot \delta = {K_E}({\delta _r}-\delta )/{T_E}\text{。} $ |
韩京清于20世纪80年代末提出了自抗扰控制技术,至今已被应用到电力系统、化工过程等其他领域,取得了显著的社会和经济效益。
自抗扰控制器包括,跟踪微分器(TD)、扩张状态观测器(ESO)和非线性误差反馈控制律(NLSEF)3部分,其核心部分是ESO,主要用于实时估计系统内部和外界干扰。本文主要对NLSEF进行改进,引入快速终端滑模面(FTSM),在幂指数趋近律的作用下,设计出有效的控制律。
针对2阶非线性系统,参考文献[10],可得到跟踪微分器的离散形式:
| $ \left\{ \begin{gathered} {\sigma _1}(k + 1) = {\sigma _1}(k) + h{\sigma _2}(k)\text{,} \\ {\sigma _2}(k + 1) = {\sigma _2}(k) + hfh \text{,} \\ fh = fhan({\sigma _1}(k)-\sigma (k),{\sigma _2}(k),r,h)\text{。} \\ \end{gathered} \right. $ | (2) |
其中:h,r分别为系统的积分步长和快速因子;σ为输入信号,σ1,σ2分别为σ的跟踪信号和跟踪微分信号,即
针对2阶非线性系统:
| $ \left\{ \begin{gathered} {{\dot x}_1} = {x_2} \text{,} \\ {{\dot x}_2} = f({x_1},{x_2}) + \omega (t) + bu(t) \text{,} \\ y = {x_1} \text{。} \\ \end{gathered} \right. $ | (3) |
式中:
令
| $ \left\{ \begin{gathered} {{\dot x}_1} = {x_2} \text{,} \\ {{\dot x}_2} = {x_3} + bu(t)\text{,} \\ {{\dot x}_3} = g \text{,} \\ y = {x_1} \text{。} \\ \end{gathered} \right. $ | (4) |
根据参考文献[11-12]可以得到系统(3)的线性扩张状态观测器(LESO)如下:
| $ \left\{ \begin{array}{l} {\mathop {\hat x}\limits^ \cdot _1} = {{\hat x}_2} - 3{\eta _0}({{\hat x}_1} - y),\\ {\mathop {\hat x}\limits^ \cdot _2} = {{\hat x}_3} - 3{\eta _0}^2({{\hat x}_1} - y) + bu(t),\\ {\mathop {\hat x}\limits^ \cdot _3} = - {\eta _0}^3({{\hat x}_1} - y). \end{array} \right. $ | (5) |
其中:
滑模变结构控制出现于20世纪60年代,通过设计滑模切换面,使得系统的状态变量沿着滑模面滑动,当系统受到参数摄动和外界干扰时,能够保持不变。正是这种特性使得其受到众多学者的重视。
针对2阶不确定非线性系统,传统终端滑(TSM)设计的切换面为
| $ u = - {b^{ - 1}}(f(x) + \beta \frac{p}{q}{x_1}^{q/p - 1}{x_2} + ({l_g} + \eta ){\mathop{\rm sgn}} (s))。 $ |
由于上述控制律中含有
为克服传统TSM带来的奇异问题及其收敛速度问题,本文引入快速终端滑模面(FTSM),不仅克服了传统滑模的奇异问题,也提高了系统的收敛速度。
| $ s = {x_2} + \alpha {x_1} + \beta {x_1}^v $ | (6) |
式中:α>0;β>0;1<v<2;x1;x2为系统的状态变量,且
结合船舶欠驱动系统(1),将船舶实际船首向和期望船首向的差值φe,即船首向误差作为系统的状态变量,变形转化为全驱动系统:
| $ \left\{ \begin{gathered} {{\dot \varphi }_e} = \dot \varphi -{{\dot \varphi }_d} \text{,} \\ {{\ddot \varphi }_e} = f(r) + \omega (t)-{{\ddot \varphi }_d} + bu \text{,} \\ y = {\varphi _e} \text{。} \\ \end{gathered} \right. $ | (7) |
式中:f(r)为系统的内部不确定扰动;ω(t)为外界风、浪和流的干扰;φd为期望船首向;φ为船舶实际船首向。
因此,可设计关于船舶船首向角误差e的FTSM:
| $ s = {\dot \varphi _e} + \alpha {\varphi _e} + \beta {\varphi _e}^v \text{。} $ | (8) |
式中参数与式(6)相同。
对式(8)求导:
| $ \begin{aligned} \dot s = & {{\dot \varphi }_e} + \alpha {\varphi _e} + \beta {\varphi _e}^v = \\ & f(r) + \omega (t)-{{\ddot \varphi }_d} + bu + \alpha {{\dot \varphi }_e} + v\beta {\varphi _e}^{v-1}{{\dot \varphi }_e} \text{。} \end{aligned} $ | (9) |
采用取幂指数趋近律,保证系统能以较大的速度趋近于滑动模态,并可有效减小系统抖振:
| $ \dot s = -\varepsilon {\left| {{s}} \right|^2}\operatorname{sgn} (s)-ks \text{,} $ | (10) |
则有:
| $ f(r) + \omega (t) \!-\! {\ddot \varphi _d} + bu \!+\! \alpha {\dot \varphi _e} \!+\! v\beta {\varphi _e}^{v-1}{\dot \varphi _e} \!=\! -\varepsilon {\left| {\text{s}} \right|^2}\operatorname{sgn} (s)-ks \text{,} $ |
整理得:
| $ u = - {b^{ - 1}}[\varepsilon {\left| s \right|^2}{\mathop{\rm sgn}} (s){\rm{ + }}ks + v\beta {\varphi _e}^{v - 1}{\dot \varphi _e} + \alpha {\dot \varphi _e} - {\ddot \varphi _d} + f(r) + \omega (t)]。 $ | (11) |
通过扩张状态观测器实时估计出船舶内部不确定扰动和外界干扰时,即
| $ {{u}} \!=\! -{b^{-1}}[Js \!+\! {\sigma _{ESO}}{\left| {{s}} \right|^2}\operatorname{sgn} (s) \!+\! v\beta {\varphi _e}^{v-1}{\dot \varphi _e} \!+\! \alpha {\dot \varphi _e} \!-\! {\ddot \varphi _d} \!+\! {\hat x_3}]\text{。} $ | (12) |
其中
对于FTSM-NLSEF控制律,引入快速终端滑模,可提高系统的收敛速度,减少原始自抗扰控制器的可调参数;采用幂指数趋近律减小了系统达到平衡状态时的抖振。本文考虑了舵机(SE)特性。图 1为考虑舵机特性后的快速终端滑模船舶曲线航迹跟踪控制器结构图。
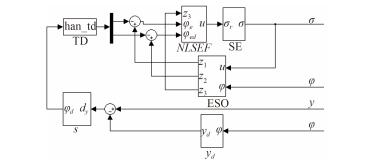
|
图 1 FTSM-ADRC控制器结构图 Fig. 1 FTSM-ADRC controller structure chart |
对于航行中的船舶,在大地坐标系下,假设其初始位置为p(x,y),其中x,y分别为船舶的纵向和横向位移,在受到风、浪和流的影响时,船首向和计划航迹向之间会形成一个风流压差角。为了使船舶沿着固定的曲线航迹行驶,构造期望船首向角方程,在确保船舶纵向和横向位置偏差
参考文献[14],构造期望船首向角方程如下:
| $ \left\{ \begin{aligned} \Delta \dot x = & u\cos \Delta \varphi -v\sin \Delta \varphi \text{,} \\ \Delta \dot y = & u\sin \Delta \varphi + v\cos \Delta \varphi \text{,} \\ \Delta \varphi = & {\varphi _d}(t)-{\varphi _p}(t) \\ {\varphi _d}(t) \!\!= & \!\! -{a_2}\!\!\!\int_0^t {\tanh [\Delta \dot y(\delta ) \!\!+\!\! {a_1}\!\!\tanh ({a_0}\Delta y)]d\delta \!\!+\!\! {\varphi _p}(t)} \text{。} \\ \end{aligned} \right. $ | (13) |
式中:∆x和∆y为船舶的位置偏差;φd为期望船首向;φp为船舶计划航迹向;a0,a1,a2为可调参数,并且a0 > 0, a1 > 0, a2 > 0。
证明:
假设
讨论:
船舶计划航迹向和其实际船首向之间的夹角∆φ,当
同理可知:当σ<0,由于
证明完毕。
由上述证明可知,当船舶偏航时,在期望船首向方程的作用下,将船舶航迹跟踪控制问题转化为航向镇定问题,纵向和横向航迹偏差收敛于0,船舶可以沿着期望的曲线航迹航行。
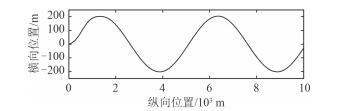
4 Simulink仿真以大连海事大学教学实习船“育龙”轮为对象,通过Simulink进行仿真实验。船舶参数为:船长126 m,型宽20.8 m,型深11.4 m,平均吃水8.8 m。船舶模型初始状态和控制器参数如下:船舶模型参数K=0.478,T=216,a=30,ω(t)=0.001,v=0.5,b=K/T;TD模块中参数r=30,h=0.05;ESO模块中参数η0=5;控制律中参数β=0.01,v=5/3,α=0.02,J=0.01,δESO=0.000 001,期望船首向角方程参数a0=0.003,a1=2.5,a2=0.001。初始条件设置为:前进速度u=7 m/s,v=0,3 m/s,船舶初始位置在原点,计划航迹为yd=200sin(0.000 4πx),即振幅200 m,当船舶纵向前进5 000 m时,完成1个周期。仿真结果如图 2~图 5所示:

|
图 2 横向位置 Fig. 2 Horizontal positions |
|
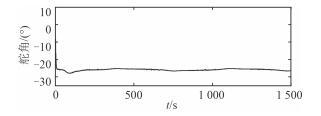
图 3 舵角 Fig. 3 Rudder angle |
|
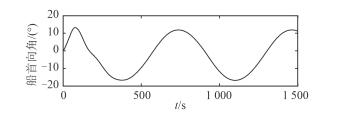
图 4 船首向角 Fig. 4 Heading angle |
|
图 5 船位 Fig. 5 Position of vessel |
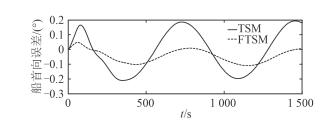
分析传统线性滑模和采用了幂指数趋近律的快速终端滑模的船首向误差如图 6所示,发现后者误差更小,提高了控制精度。
|
图 6 船首向角误 Fig. 6 Heading angle error |
为了简化船舶控制系统并改善其性能,在自抗扰控制器的非线性误差状态反馈模块引入快速终端滑模,确保误差较大时能快速趋于平衡状态,提高了系统状态的收敛速度,减少了可调参数;结合幂指数趋近律,减小了滑模的固有抖振,改善了系统性能。根据仿真图像,当船舶受到恒定外界干扰时,在FTSM-ADRC控制律的作用下,船舶能跟踪期望曲线轨迹,控制器效果良好,具有较强的鲁棒性。
| [1] |
郭晨, 汪洋, 孙富春, 等. 欠驱动水面船舶运动控制研究综述[J]. 控制与决策 , 2009, 24 (3) :321–329.
GUO Chen, WANG Yang, SUN Fu-chun, et al. Survey for motion control of underactuated surface vessels[J]. Control and Decision , 2009, 24 (3) :321–329. |
| [2] | DO K D, JIANG Z P, PAN J, et al. A global output-feedback controller for stabilization and tracking of underactuated ODIN: a spherical underwater vehicle[J]. Automatica , 2004, 40 (1) :117–124. DOI:10.1016/j.automatica.2003.08.004 |
| [3] |
曾薄文, 朱齐丹, 于瑞亭. 欠驱动水面船舶的曲线航迹跟踪控制[J]. 哈尔滨工程大学学报 , 2011, 32 (10) :1317–1322.
ZENG Bo-wen, ZHU Qi-dan, YU Rui-ting. Curve tracking control of an underactuated surface vessel[J]. Journal of Harbin Engineering University , 2011, 32 (10) :1317–1322. |
| [4] |
孟威, 郭晨, 孙富春, 等. 欠驱动水面船舶的非线性滑模轨迹跟踪控制[J]. 哈尔滨工程大学学报 , 2012, 33 (5) :585–589.
MENG Wei, GUO Chen, SUN Fu-chun, et al. Nonlinear sliding mode tracking control of underatuated surface vessels[J]. Journal of Harbin Engineering University , 2012, 33 (5) :585–589. |
| [5] |
朱齐丹, 于瑞亭, 刘志林. 欠驱动船舶全局K指数航迹跟踪的级联反步法[J]. 船舶工程 , 2012, 34 (1) :47–51.
ZHU Qi-dan, YU Rui-ting, LIU Zhi-lin. Cascaded backstepping approach for global K-exponential tracking control of an underactuated surface vessel[J]. Ship Engineering , 2012, 34 (1) :47–51. |
| [6] |
韩冰, 赵国良. 基于微分平滑的欠驱动船舶航迹控制[J]. 哈尔滨工程大学学报 , 2004, 25 (6) :709–713.
HAN Bing, ZHAO Guo-liang. Path tracking control of underactuated surface vessels based on the differential flatness[J]. Journal of Harbin Engineering University , 2004, 25 (6) :709–713. |
| [7] |
卜仁祥.欠驱动水面船舶非线性反馈控制研究[D].大连:大连海事大学, 2008.
BU Ren-xiang. Nonlinear feedback control of underactuated surface ships[D]. Dalian: Dalian Maritime University, 2008. http://cdmd.cnki.com.cn/article/cdmd-10151-2008210036.htm |
| [8] |
胡江强.基于遗传优化的船舶航向混合智能控制[D].大连:大连海事大学, 2003.
HU Jiang-qiang. Genetic-based hybrid intelligent control for ship steering[D]. Dalian: Dalian Maritime University, 2003. http://cdmd.cnki.com.cn/article/cdmd-10151-2005129670.htm |
| [9] |
霍学亮, 任光, 张均东, 等. 基于Simulink的船舶舵机系统的建模与动态仿真[J]. 大连海事大学学报 , 2007, 33 (S1) :74–76.
HUO Xue-liang, REN Guang, ZHANG Jun-dong, et al. Modeling and dynamic simulation of steering gear system of ship based on simulink[J]. Journal of Dalian Maritime University , 2007, 33 (S1) :74–76. |
| [10] |
韩京清.
自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008 : 66 -69.
HAN Jing-qing. Active disturbance rejection control technique——the technique for estimating and compensating the uncertaintics[M]. Beijing: National Defense Industry Press, 2008 : 66 -69. |
| [11] | GAO Z Q. Active disturbance rejection control: A paradigm shift in feedback control system design[C]//Proceedings of the 2006 American control conference. Minneapolis, MN: IEEE, 2006: 2399-2405. |
| [12] | GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American control conference. Denver, CO, USA: IEEE, 2003: 4989-4996. |
| [13] |
张巍巍, 王京. 基于指数趋近律的非奇异Terminal滑模控制[J]. 控制与决策 , 2012, 27 (6) :909–913.
ZHANG Wei-wei, WANG Jing. Nonsingular terminal sliding model control based on exponential reaching law[J]. Control and Decision , 2012, 27 (6) :909–913. |
| [14] |
李荣辉, 李铁山, 卜仁祥. 欠驱动水面船舶航迹跟踪自抗扰控制[J]. 大连海事大学学报 , 2013, 39 (2) :5–8.
LI Rong-hui, LI Tie-shan, BU Ren-xiang. Active-disturbance-rejection control based underactuated surface vessel path following[J]. Journal of Dalian Maritime University , 2013, 39 (2) :5–8. |
 2016, Vol. 38
2016, Vol. 38
