1. 中国计量学院 浙江流量计量技术重点实验室, 浙江 杭州 310018
;
2. 浙江水利水电学院 机械与汽车工程学院, 浙江 杭州 310018
收稿日期: 2016-02-02, 修回日期: 2016-03-15.
基金项目: 浙江省自然科学基金资助项目(Y14E090034,Y13F020140);浙江省青年科学家培养计划资助项目(2013R60G7160040)
作者简介: 谢卓(1990-), 男, 硕士研究生, 研究方向为流体检测与仿真技术
1. Zhejiang Provincial Key Laboratory of Flow Measurement Technology, China Jiliang University, Hangzhou 310018, China
;
2. Zhejiang Water Conservancy and Hydropower College, Mechanical and Automotive Engineering, Hangzhou 310018, China
0 引言 作为海洋石油、天然气资源开发的重要基地,海洋平台的开发、研究和利用越来越受到人们的广泛关注[1];从渤海2号被推倒,我国相继开展了对于固定式平台的研究并取得一系列研究成果。近海结构的受力研究是海洋工程领域的重要专题,田宏升[2]研究计算了小构件的波浪载荷。张金平[3]综述了近年来海洋平台波浪理论及波浪载荷计算方法的研究与发展概况。何懋华[4]分析研究了冰载荷作用下的固定式平台的极限承载能力以及波浪荷载作用下的固定式平台的极限承载能力。刘为民等[5]从入射波角度、波高以及周期方面探讨了规则波下张力腿平台的动力特性。Sang-Yun BAE[6]采用高阶边界元法对非线性波浪流共同作用下的FPSO进行了数值模拟,并对衍射和辐射波进行了时域计算。Jimmy Ng K.T等[7]于2010年对只有在波、流以及波流联合作用下的多立柱进行试验并进行频谱、受力分析,研究了上游立柱尾流对下游立柱的影响及下游立柱的动力响应。海洋平台结构的可靠性尤为重要。一旦结构失效,不仅会造成巨大的经济损失,而且还会有严重的人员伤亡和环境污染[8-10]。
本文从动力学的角度分析时域内结构的响应特征,以不同的入射波作为激励条件,分析比较结构的位移、速度以及加速度响应,并得出一些有意义的结论,从而可以为固定式海洋平台的相关设计提供理论计算依据。
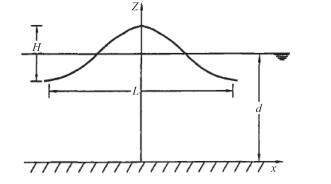
1 理论分析 Airy线性波理论是波浪理论中最基本最常用的波浪理论。Airy波浪理论将非线性的波浪自由面条件,近似以线性的边界条件代替,这一线性边界适应于波高很小的情况。Airy线性波的速度势为:
|
$
\varphi (x,t) = \frac{{gH}}{{2\omega }}\frac{{\cos h kz}}{{\cos h kd}}\sin (kx-\omega t)\text{,}
$
|
(1) |
波面表达式为:
|
$
\eta (x,t) = \frac{H}{2}\cos (kx-\omega t)\text{,}
$
|
(2) |
式中:H为波高;k为波数,k=2π/L;L为波长;d为水深。
|
$
L = T\sqrt {\frac{{gL}}{{2{\rm{\pi }}}}\tan h\frac{{2{\rm{\pi }}d}}{L}} 。
$
|
(3) |
设θ=kx-ωt,由线性波速度势可以得到波浪水质点速度和加速度的表达式为:
|
$
u = \frac{{\partial \varphi }}{{\partial x}} = \frac{{gkH}}{{2\omega }}\frac{{\cos h kz}}{{\cos h kd}}\cos \theta \text{,}
$
|
(4) |
|
$
\mathop u\limits^. = \frac{{\partial u}}{{\partial t}} = \frac{{gkH}}{2}\frac{{\cos h kz}}{{\cos h kd}}\sin \theta \text{。}
$
|
(5) |
莫里森方程作为计算海洋结构物上波浪力的常用方法,其计算的波浪力包括与水平速度的平方成正比的阻力项以及与水平加速度成正比的惯性力项。阻力项是由于水质点的速度引起的,而惯性力项则是由于水质点的加速度引起的。其表达式为:
|
$
f = {C_M}{A_I}\mathop u\limits^. + {C_D}{A_D}u\left| u \right| \text{。}
$
|
(6) |
式中: AI=0.25 ρπD2;AD=0.5 ρD;CD和CM为拖曳力系数和惯性力系数;D为桩柱直径;u为海水质点水平速度;$ \mathop u\limits^. $为海水质点的水平加速度。
将式(4)和式(5)带入式(6),整理得到线性波理论波浪力的表达式为:
|
$
\begin{array}{*{20}{c}}
{f(x,t) = {C_M}{A_I}\frac{{gkH}}{2}\frac{{\cos hkz}}{{\cos hkd}}\sin \theta + }\\
{\sqrt {\frac{8}{{\rm{\pi }}}} {C_D}{A_D}{\sigma _u}\frac{{gkH}}{{2\omega }}\frac{{\cos hkz}}{{\cos hkd}}\cos \theta ,}\\
{f(x,t) = {C_M}{A_I}gk\frac{{\cos hkz}}{{\cos hkd}}\eta (x,t + T/4) + }\\
{\sqrt {\frac{8}{{\rm{\pi }}}} {C_D}{A_D}{\sigma _u}\frac{{gk}}{\omega }\frac{{\cos hkz}}{{\cos hkd}}\eta (x,t)}
\end{array}{\rm{ }}
$
|
(7) |
式中:
|
$
\sigma _{{u}}^2 = \int_0^\infty {{{(\omega \displaystyle\frac{{\cosh kz}}{{\sinh kh}})}^2}{S_\eta }(\omega )} {\rm d}\omega
$
|
式(7)同样适用于不规则的波浪场,可以将不规则的波浪场的波面表达函数η(x,t)看作是多个不同频率和不同幅值的规则波浪场相叠加的结果。对波浪力f(x,t)进行积分,可求得整根柱体上所受的波浪力。
固定式平台的振动方程为
|
$
M\ddot Y + C\dot Y + KY = P(t)。
$
|
(8) |
式中:M为质量矩阵;$ \ddot Y $为广义振动加速度列阵;C为阻尼系数矩阵;$ \dot Y $为广义振动速;Y为振动位移偏移量;K为结构刚性矩阵。
采用模态叠加法求解振动位移响应,通过各个模态振动响应的叠加可求得几何坐标表示的位移即y1=y1(t)和y2=y2(t)解。其中λdi和λi分别为有阻尼固有频率和无阻尼固有频率,ξi为结构阻尼比。
|
$
y(t) = \sum\limits_{i = 1}^n {{\phi _i}{q_i}(t)} \text{,}
$
|
(9) |
进一步可求得平台振动的速度和加速度为:
|
$
v(t) = \sum\limits_{i = 1}^n {{\phi _i}{{\mathop q\limits^. }_i}(t)} \text{,}
$
|
(10) |
|
$
a(t) = \sum\limits_{i = 1}^n {{\phi _i}{{\mathop q\limits^{..} }_i}(t)} \text{。}
$
|
(11) |
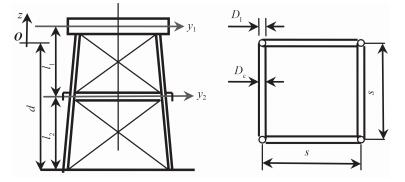
2 算例分析 以一简化的具有上下2层甲板的固定平台为算例,文中不牵涉流载荷分布问题,故简化为2层甲板完全可取。其结构示意图如图 2所示,工作水深为d,集中质量到上下2层甲板,其中2层甲板质量为m1和m2,平台具有2个质量独立的响应位移分别为y1和y2。
2.1 参数设置 算例采用固定式平台的参数如表 1所示,其中Kij为平台的刚度系数,ξ为阻尼比,Nl=4表明平台为四垂直立柱架构,Nc=2为平台的2个平行支撑。采用的入射波参数如表 2所示。由表 1和表 2可知:此平台垂直立柱外径Dl=5.5 m,入射波波长Lw>224 m,Dl/Lw<0.024<0.2,满足Morison方程的使用条件。结构的直径尺寸相对于波浪要小得多,假设结构的运动相对于波浪的运动小得多,这样Morison方程中的惯性系数CM和流体阻力中的CD相比,前者处于主导地位,即惯性体系下,流体流动占主导地位。
表 1(Tab. 1)

表 1 固定式平台参数
Tab. 1 stationary platform parameters
| 平台参数 |
| m1/kg |
4.69 E + 06 |
| K11/N·m–1 |
7.35 E + 07 |
| K12=K21/N·m–1 |
–1.15 E + 08 |
| l1=l2/m |
38 |
| Nl |
4 |
| Dl /m |
5.5 |
| s/m |
30 |
| m2/kg |
3.13 E + 06 |
| K22/N·m–1 |
3.59 E + 08 |
| d/m |
61 |
| Dc /m |
4.3 |
| Nc |
2 |
| ξ1=ξ2 |
0.05 |
|
表 1 固定式平台参数
Tab.1 stationary platform parameters
|
表 2(Tab. 2)

表 2 波浪参数
Tab. 2 Wave parameters
| 参数 |
波浪 |
| η1 |
η2 |
η3 |
| 波高H/m |
12.5 |
16.6 |
20.8 |
| 周期T/s |
12.39 |
14.07 |
15.9 |
| 波数k/m–1 |
0.028 |
0.023 |
0.019 |
| 波长L/m |
224.243 |
273.471 |
325.818 |
|
表 2 波浪参数
Tab.2 Wave parameters
|
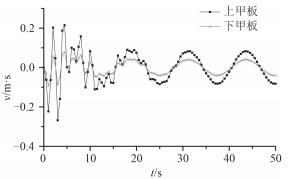
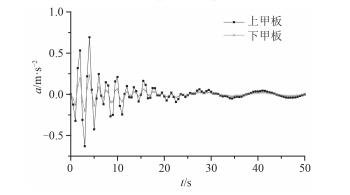
2.2 计算结果 以规则波为入射波,根据某海域气象资料,取波浪周期12.39 s,波高12.5 m,计算得到波长L=224.243 m,如表 2中η1所示,进行计算并得到平台上甲板和下甲板的位移y、速度v及加速度a,对比得到结果如图 4~图 6所示。
由图 4-图 6可以观察到,平台架构的位移响应、速度响应及加速度响应在经过2个波浪周期时间的振荡后逐渐趋于稳定,且响应均在t=4 s时达到峰值。同一时刻平台上甲板的位移响应、速度响应和加速度响应均要大于下甲板的。由此得出,平台在某一特定入射波激励下上甲板的振动相比下甲板更为剧烈。
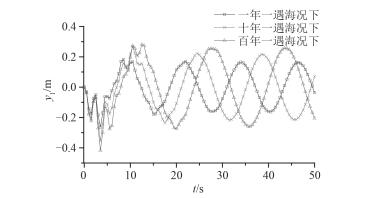
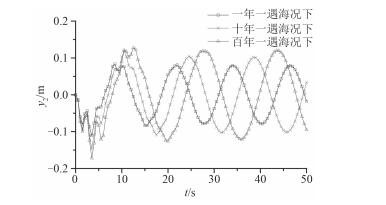
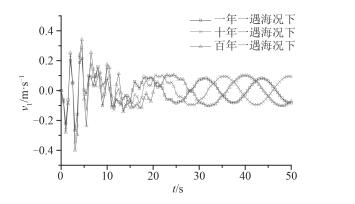
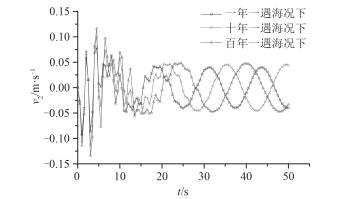
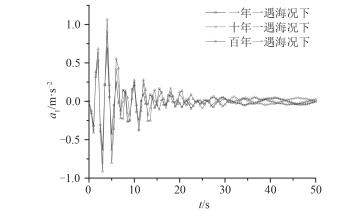
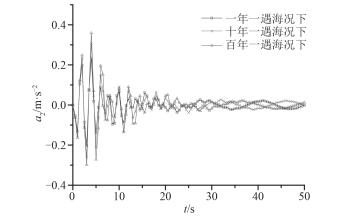
采用3种不同条件的规则波为入射波进行计算,3种波浪即表 2中的η1,η2及η3,周期及波高等参数如表 2所列。计算得到平台结构的位移响应,速度响应以及加速度响应,所得结果如图 7~图 12所示。
以3种不同条件的规则波为入射波,由上、下甲板的位移响应对比图 7和图 8可知,结构上甲板和下甲板的位移响应均在t=4 s处达到峰值,且波浪η1激励下位移响应峰值最大,波浪η3激励下最小;由图 9和图 10可以看出结构上甲板和下甲板的速度响应均在t=3 s处达到响应峰值,且3种波浪条件中η3激励下的平台速度响应峰值大于其它波浪条件激励下的响应,η1时响应的峰值最小;由图 11和图 12得到结构上、下甲板的加速度响应均在t=4 s处达到响应峰值,且同位移响应和速度响应一样,波浪η3激励下的加速度响应峰值最大,η1时的响应峰值最小。综上可得结构的位移响应、速度响应及加速度响应随着入射波强度的增大而趋于增大,故随着入射波强度的增大,结构的振动也变得更为剧烈。
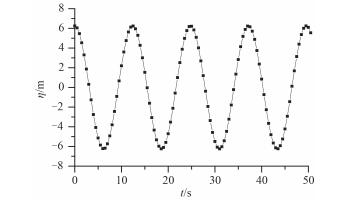
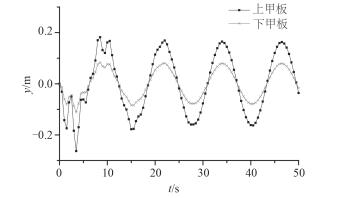
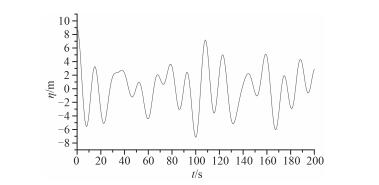
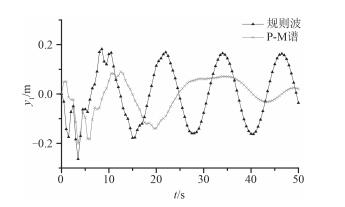
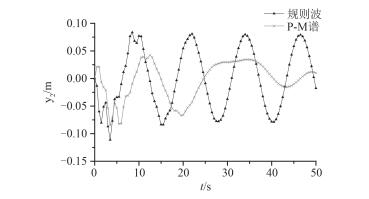
Pierson-Moskowitz波高谱于1966年被国际船模水池会议定为标准海浪谱,目前广泛应用于海浪研究及有关工程问题。采用以P-M谱为随机波浪谱作为入射波,取波浪周期12.39 s,有义波高12.5 m,其波面高程如图 13所示。计算结构位移、速度和加速度响应并与同条件下以规则波为入射波所得振动响应结果进行比较,限于篇幅这里仅给出位移响应的对比结果,如图 14和图 15所示。
由图 14和图 15上、下甲板位移响应对比可看出在周期相同,并取有义波高与规则波波高相同的2种不同入射波激励时,结构位移响应会在同一时刻达到峰值,且以规则波为入射波时的位移响应峰值要大于P-M谱激励下的位移响应峰值。由此可知,结构在规则波的激励下的振动响应要比相同强度以P-M谱为随机波浪谱的振动响应更为剧烈。综上所述,结构的振动响应不仅与入射波的周期和波高有关,与波浪的形式也有一定的关系。
3 结语 本文分析了固定式平台的振动响应问题,将立柱上分布的波浪力处理为集中作用在上甲板和下甲板2个结点上的集中载荷。对比分析了上、下甲板的振动响应;研究了以不同海况(一年一遇,十年一遇和百年一遇)的规则波为入射条件,固定式平台结构的响应以及相同海况不同形式入射波(规则波和以P-M谱为随机波浪谱)下结构的运动响应。主要结论如下:平台在入射波激励下上甲板比下甲板的振动更为剧烈;随着入射波强度的增大,结构的振动也变得更为剧烈;结构的振动响应不仅与入射波的周期和波高有关,与波浪的形式也有一定的关系。
 2016, Vol. 38
2016, Vol. 38
