气层减阻技术可大幅降低船舶阻力,是实现我国航运业节能减排新目标的重要途径。相对于模型试验,目前气泡船的数值研究相对较少,以下学者开展了有意义的研究:Jin-Keun Choi等[1]联合采用面元法与求解UN-RANS(Unsteady Reynolds Averaged Navier-Stokes equation)的方法分别计算了喷气下瘦长型船的兴波、船底气层形态、粘性阻力;D.Kim等[2]采用直接数值模拟(DNS)的方法计算了断阶后气层的非定常流动形态,并与试验结果进行对比,数值结果较为精确的与试验结果吻合;Hoang Cong Liem等[3]结合边界层积分方程及经验公式,计算了喷气对船舶阻力的影响,该方法可用于计算实尺度气泡船的减阻效果;李云波等[4-6]基于势流理论,采用边界元方法计算了船底凹槽内的气层形态;王家楣等[7]基于PHOENICS软件中的IPSA(相间滑移模型)计算了二维气泡船的喷气减阻效果,计算结果与试验结果在趋势上一致;蔡红玲等[8-10]开展了高速气泡船流场数值模拟,在Fluent平台上采用气液两相流模型进行计算,所得结果在规律上合理,但是由于在船体表明仅采用非结构网格,因而不能较好地模拟边界层流动。
上述研究均为湍流模型、网格、壁面函数等进行系列探讨,所得结果尚需提高。本论文针对气液混合流,系统研究湍流模型、网格、壁面函数对计算结果的影响,最终形成可较好模拟气液混合流的数值方案,对肥大型气泡船气层形态及减阻率预报具有指导意义。
1 Mixture两相流模型Mixture模型的控制方程由连续性方程和动量方程构成,其具体表达形式如下:
连续性方程为:
| $ \frac{\partial }{{\partial t}}({\rho _m}) + \nabla \cdot ({\rho _m}{\vec v_m}) = 0 \text{,} $ | (1) |
其中
| $ {\vec v_m} = \frac{{\sum\limits_{k = 1}^n {{\alpha _k}{\rho _k}{{\vec v}_k}} }}{{{\rho _m}}} \text{。} $ | (2) |
式中:
混合相的动量方程由各分相的动量方程相加得到,可表示为:
| $ \begin{aligned} \frac{\partial }{{\partial t}}({\rho _m}{{\vec v}_m}) \!+\! \nabla \! \cdot \!({\rho _m}{{\vec v}_m}{{\vec v}_m}) \!=\! -\nabla p \!+\! \nabla \cdot [{\mu _m}(\nabla {{\vec v}_m} \!+\! \nabla \vec v_m^T)] + \\ \quad \quad \quad \quad \quad {\rho _m}\vec g + \vec F + \nabla \cdot (\sum\limits_{k = 1}^n {{\alpha _k}{\rho _k}} {{\vec v}_{dr,k}}{{\vec v}_{dr,k}}) \text{。} \\ \end{aligned} $ | (3) |
式中:n为混合流中相的数量;
| $ {\mu _m} = \sum\limits_{k = 1}^n {{\alpha _k}{\mu _k}} \text{,} $ | (4) |
| $ {v_{dr,k}} = {\vec v_k}-{\vec v_m} \text{。} $ | (5) |
式中:
该模型同时考虑了相间的滑移速度,即第p相相对于第q相的滑移速度
| $ {\vec v_{pq}} = \frac{{{\tau _p}}}{{{f_{drag}}}} \cdot \frac{{({\rho _p}-{\rho _m})}}{{{\rho _p}}}\vec a \text{,} $ | (6) |
| $ {\tau _p} = \frac{{{\rho _p}d_p^2}}{{18{\mu _q}}} \text{。} $ | (7) |
式中:
| $ \vec a = \vec g-({\vec v_m} \cdot \nabla ){\vec v_m}-\frac{{\partial {{\vec v}_m}}}{{\partial t}} \text{。} $ | (8) |
式中:
| $ {f_{drag}} = \left\{ \begin{gathered} 1 + 0.15{{Re} ^{0.687}} \text{,} \quad {Re} \leqslant 1000 \text{,} \\ 0.0183{Re} \text{,} \quad \quad \;\;\;{Re} > 1000 \text{。} \\ \end{gathered} \right.\quad \; $ | (9) |
采用光滑平板为对象研究气液混合流数值模型的构建方法。平板的外形及尺寸如图 1所示。平板总长1 200 mm,宽380 mm,厚度10 mm,在距离头部410 mm处安装喷气板。喷气板宽120 mm,长70 mm。

|
图 1 计算平板主尺度示意图 Fig. 1 The main parameters of plate |
计算流域的网格布局如图 2所示。流域总长为6倍板长,总宽为4倍板宽。流域入口距离平板头部1倍板长,设置为速度入口;出口距离平板尾部4倍板长,为静压力出口;喷气入口设置为质量流量入口。由于气体不可压缩,则根据质量流量可换算得到相应的体积流量。

|
图 2 平板流场区域及网格布局 Fig. 2 The flow field of plate and its mesh distribution |
众多研究表明[11-15]:只有当气泡分布在湍流边界层内时才具备较好的减阻效果,因此采用Mixture模型计算混合流边界层时,壁面附近网格的处理方法较为关键。
目前,在船舶粘性流场计算中,壁面的处理方法主要有标准壁面函数法、增强壁面函数法及无壁面函数的直接计算方法。
根据湍流模型、壁面函数的自身特征以及数值计算经验,壁面附近网格的处理办法一般基于如下原则:
1)标准壁面函数法。y+应大于30~60,最好接近30,湍流边界层内应布置一定的网格数量。标准壁面函数不适用于层流底层,因此第1层网格应布置在对数律层内。
2)增强壁面函数法。该方法可用于计算层流底层的流动,当用于计算层流底层时,y+最好取值为1左右,但如果第1层网格布置在了层流层内,略高的y+值也可行。计算过程中,层流底层内应布置至少10个网格节点。
3)对于S-A模型(Spalart-Allmaras),若采用增强壁面函数,则y+=1;若采用标准壁面函数,则y+>30。
4)对于低雷诺数k-ω模型,网格要求与增强壁面函数相同;采用高雷诺数k-ε模型时,网格要求与标准壁面函数相同。
5)对于LES模型,壁面附近的网格要求与增强壁面函数的要求相同。
本文计算了8种壁面函数及湍流模型的组合方案,如表 1所示。表中y+值所对应的来流速度为1.241 m/s。
|
|
表 1 湍流模型及壁面函数 Tab.1 The turbulence models and wall functions |
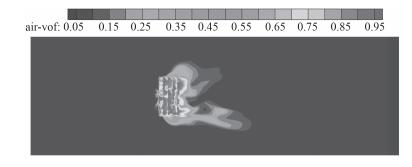
采用上述湍流模型及壁面函数计算了气流量Q=0.5 m3/h,速度V=1.241 m/s时平板底部的气层形态,所得结果如图 3~图 10所示。图 11为相同气流量及来流速度下气层的模型试验观测结果。
|
图 3 计算方案1(S-A模型,y+=3) Fig. 3 The first calculation case by S-A turbulence model at y+=3 |

|
图 4 计算方案2(S-A模型,y+=10) Fig. 4 The second calculation case by turbulence S-A model at y+=10 |
|
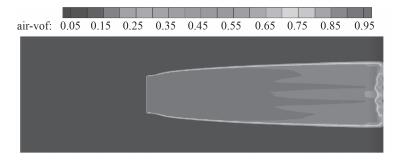
图 5 计算方案3(k-ω模型) Fig. 5 The third calculation case by k-ω model |

|
图 6 计算方案4(LES模型) Fig. 6 The fourth calculation case by LES model |
|
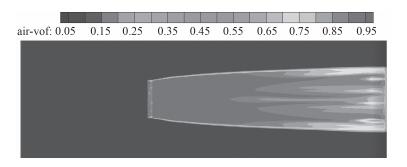
图 7 计算方案5(RNG k-ε模型及增强壁面函数,y+=2) Fig. 7 The fifth calculation case by RNG k-ε model and enhance wall function at y+=2 |
|
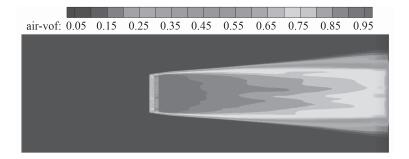
图 8 计算方案6(RNG k-ε模型及增强壁面函数,y+=10) Fig. 8 The sixth calculation case by RNG k-ε model and enhance wall function at y+=10 |
|
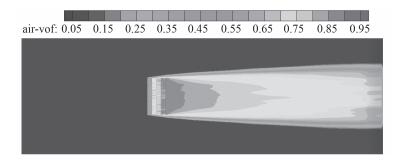
图 9 计算方案7(RNG k-ε模型及增强壁面函数,y+=20) Fig. 9 The seventh calculation case by RNG k-ε model and enhance wall function at y+=20 |

|
图 10 计算方案8(RNG k-ε模型及标准壁面函数,y+=30) Fig. 10 The eighth calculation case by RNG k-ε model and standard wall function at y+=30 |

|
图 11 平板底部气层模型试验照片 Fig. 11 The air layer photo under plate of test result |
从气层的分布上看:计算方案1与计算方案3所得结果与试验结果在变化规律上相差甚远,说明使用S-A模型与LES模型模拟气液混合流时具有较大局限性,在本文建立的网格方案下,尚需进行优化。计算方案2、方案4~方案8在气层的分布规律上与试验结果较一致,但各方案之间存在差别。
从气泡浓度与气层流态上看:计算方案2、方案3与方案5所得气体在壁面上的分布浓度大于0.95,平板表面上几乎形成了分层流;计算方案7与计算方案8所得气体在壁面上的浓度为0.5~0.8,主要为气体与液体的混合流动。从图 11的试验图片可以看出:气体主要气泡群的形式存在,未形成分层流。说明计算方案7或计算方案8所得结果与试验结果较为接近。
从图 7~图 9(计算方案5~方案7)还可以看出:在湍流模型及壁面函数不变的情况下,壁面法向的第1层网格厚度(y+值)对平板表面气泡浓度的计算结果有较大影响。当气流量及来流速度相同时,第1层网格厚度增加,壁面上的气泡浓度降低。
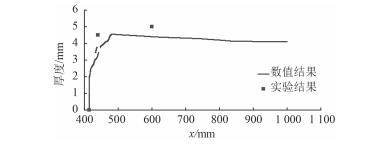
3.2 气层厚度及宽度采用3.1节的计算方案8计算不同流动工况下平板底部的气层,并将计算所得气层厚度与实验结果进行对比(试验中气层厚度的测量见文献[6]),如图 12~图 14所示。图中横坐标x表示与平板头部的距离,其中x=415 mm处为喷气入口;纵坐标表示沿流动方向不同位置处的气层厚度。
|
图 12 V=1.287 m/s,Q=1.08 m3/h气层厚度沿平板长度方向变化的计算值与实验结果 Fig. 12 The air layer thickness of numerical results and test result at V=1.287 m/s and Q=1.08 m3/h |
|
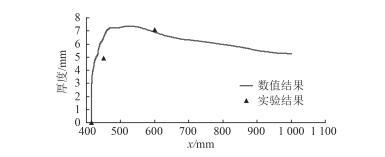
图 13 V=0.838 m/s,Q=1.11 m3/h气层厚度沿平板长度方向变化的计算值与实验结果 Fig. 13 The air layer thickness of numerical result and test result at V=0.838 m/s and Q=1.11 m3/h |
|
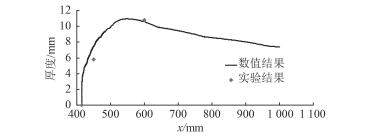
图 14 V=1.287 m/s,Q=2.061 m3/h气层厚度沿平板长度方向变化的计算值与实验结果 Fig. 14 The air layer thickness of numerical result and test result at V=1.287 m/s and Q=2.06 m3/h |
从图 12~图 14可看出,采用Mixture两相流模型与RNG k-ε湍流模型相结合的数值方法,可有效模拟气层厚度沿流动方向的变化规律。
图 15和图 16给出了不同流动工况下气层宽度数值计算结果与实验结果的对比。图中x=0 mm处为喷气入口;纵坐标表示在流动方向上的气层宽度。

|
图 15 V=1.287 m/s,Q=2.061 m3/h沿平板长度方向气层厚度的计算值与实验结果 Fig. 15 The air layer thickness of numerical result and test result at V=1.287 m/s and Q=2.06 m3/h |

|
图 16 V=0.837 m/s,Q=1.04 m3/h沿平板长度方向气层厚度的计算值与实验结果 Fig. 16 The air layer thickness of numerical result and test result at V=0.837 m/s and Q=1.04 m3/h |
从图 15和图 16可看出:采用Mixture模型与RNG k-ε湍流模型相结合的数值方法可有效模拟气层沿平板宽度方向的扩散边界。
4 结语1)采用RNG k-ε湍流模型、标准壁面函数、第1层网格1 mm、y +为31~35的计算方案可较好地模拟平板底部气液混合层的宏观形态。
2)采用Mixture模型与RNG k-ε湍流模型相结合的方法可有效模拟气层沿平板宽度方向的扩散边界和气层厚度沿流动方向的变化规律,说明搞方法对模拟气液混合流气层形态有效。
| [1] | CHOI J K, HSIAO C T, CHAHINE G L. Numerical studies on the hydrodynamic performance and the startup stability of high speed ship hulls with air plenums and air tunnels[C]//Proceedings of the Ninth International Conference on Fast Sea Transportation FAST2007. Shanghai, China, 2007: 476-484. |
| [2] | KIM D, MOIN P. Direct numerical Simulation of air layer drag reduction over a backward-facing step[C]//Proceedings of the 63rd annual Meeting of the APS Division of Fluid Dynamics. Long Beach, California: American Physical Society, 2010: 351-363. |
| [3] | LIEM H C, TODA Y, SANADA Y. A consideration on drag reduction by air lubrication using integral type boundary layer computation[J]. Journal of the Japan Society of Naval Architects and Ocean Engineers , 2011, 13 :59–65. DOI:10.2534/jjasnaoe.13.59 |
| [4] | LI Y B, WU X Y, MA Y, et al. A method based on potential theory for calculating air cavity formation of an air cavity resistance reduction ship[J]. Journal of Marine Science and Application , 2008, 7 (2) :98–101. DOI:10.1007/s11804-008-7077-x |
| [5] | 吴晓宇.气泡船大尺寸多凹槽稳定气穴形成理论研究[D].哈尔滨:哈尔滨工程大学, 2008. http://cdmd.cnki.com.cn/article/cdmd-10217-2009060258.htm |
| [6] | 董文才, 郭日修, 朱凤荣, 等. 平板湍流边界层内气泡流流动实验研究[J]. 海军工程大学学报 , 2001, 13 (3) :34–37. |
| [7] | 郑晓伟, 王家楣, 曹春燕. 二维船舶微气泡减阻数值模拟[J]. 船舶工程 , 2005, 27 (6) :15–18. |
| [8] | 蔡红玲.高速气泡船流场数值模拟[D].武汉:武汉理工大学, 2008. |
| [9] | 杨鹏.气泡船三维粘性绕流的数值模拟[D].武汉:武汉理工大学, 2008. http://cdmd.cnki.com.cn/article/cdmd-10497-2008109663.htm |
| [10] | 曹春燕.船舶微气泡减阻数值模拟[D].武汉:武汉理工大学, 2003. http://cdmd.cnki.com.cn/article/cdmd-10497-2003095411.htm |
| [11] | 荒賀浩一, 松井良輔, 脇本辰郎, 等. 界面活性剤水溶液の水平円管内流れに及ぼす微細気泡の影響[J]. 実験力学 , 2010, 10 (3) :304–311. |
| [12] | 梁志勇, 陈池. 微气泡对平板摩擦阻力影响的分析[J]. 上海大学学报(自然科学版) , 2002, 8 (3) :267–272. |
| [13] | FELTON K, LOTH E. Diffusion of spherical bubbles in a turbulent boundary layer[J]. International Journal of Multiphase Flow , 2002, 28 (1) :69–92. DOI:10.1016/S0301-9322(01)00060-X |
| [14] | 郭峰, 欧勇鹏, 董文才, 等. 平板微气泡减阻预报及影响因素研究[J]. 中国造船 , 2008, 49 (S) :66–74. |
| [15] | MORIGUCHI Y, KATO H. Influence of microbubble diameter and distribution on frictional resistance reduction[J]. Journal of Marine Science and Technology , 2002, 7 (2) :79–85. DOI:10.1007/s007730200015 |
 2016, Vol. 38
2016, Vol. 38
