随着海洋资源开发和海洋科学的不断发展,深海无人遥控潜水器(ROV)的应用越来越广泛,在深海作业过程中由于缆索断裂导致ROV丢失的现象时有发生。母船随海面波浪做升沉运动,在一定的海况条件下,导致缆索张紧松弛状态交替出现,从而产生瞬时张力过大的情况,因而分析导致缆索张力过大的参数空间对ROV安全作业十分有必要。在实际作业中,海浪具有随机性[1],同时,缆索在张紧松弛不同阶段的刚度以及ROV在2个方向运动时受到的流体阻力是非光滑的[2],目前对缆索动力响应的研究都没有涉及这两方面的因素,因而结论与实际偏差较大。
对缆索突变载荷的研究方面,Vassalos和Huang等[3]深入分析了谐波激励下的缆索系统突变载荷,Tjavaras[4]解释了波浪激励下缆索系统突变载荷出现的机理。Niedzwecki和Thampi[5]基于单自由度模型对缆索系统的载荷进行了预估。Koh等[6]基于改进的有限差分法对低张力缆的动力学行为进行了研究。Driscoll等[7]对缆索系统在波浪激励下产生的突变载荷做了大量的工作。Hennessey等[8]对低张力缆突变载荷进行了实验研究。
本文考虑表面随机波的激励以及缆索刚度、流体阻力的非连续变化,建立ROV作业系统的以为动力学方程,并做无因次分析,因为其强非线性的特点,因而通过数值方法进行求解,得到出现突变载荷的参数空间,对ROV作业中避开不利因素,保证安全作业起到指导意义。
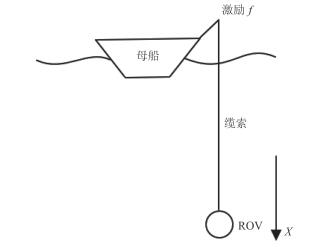
1 缆索动力学模型 1.1 ROV作业系统运动模型ROV作业系统,由母船、缆索和ROV三部分组成,如图 1所示。考虑ROV作业时缆索的动态响应,建立一维垂向运动方程,在缆索张紧阶段,ROV受到缆索的张力与非线性的流体阻力,在缆索松弛阶段,缆索张力为0。缆索上端与母船相连,受到波浪提供的激励项f,为便于分析,忽略缆索张力对母船运动的影响并假定母船运动与波浪运动一致。可以得到ROV作业时的运动方程:
|
图 1 ROV-母船作业系统示意图 Fig. 1 Sketch of cable-body system |
| $ m\ddot x + c\dot x|\dot x| + kx = w + kf\text{,} $ | (1) |
其中:
| $ k = \left\{ {\begin{array}{*{20}{c}} {\frac{{ES}}{L}\;\;\;x-f > 0}\text{,} \\ {0\;\;\;x-f \leqslant 0} \text{。} \end{array}} \right. $ |
式中:m包括ROV质量以及附加质量;x为相对于初始位置的位移,向下为正方向;c为非线性流体阻力系数;E,S和L分别为缆索的杨氏模量、横截面积及长度;w为ROV的水下重量;f为波浪的运动函数。
1.2 运动方程无因次化为了便于分析缆索的张紧松弛状态,把缆索的伸缩量Y=x-f作为变量进行求解,并且对运动方程(1),引入下列无因次参数:
| $ \begin{array}{*{20}{c}} {y = \frac{Y}{{0.5H}},\;\;{y_s} = \frac{w}{{0.5HES/L}},\;\;\tau = \frac{{2\pi t}}{T},}\\ {{\omega _n} = \sqrt {\frac{{ES/L}}{m}} ,\;\;\eta = \frac{{2\pi }}{{T{\omega _n}}},\;\;\zeta = \frac{{ca\pi }}{{T\sqrt {mES/L} }}。} \end{array} $ |
得到运动方程无因次的形式:
| $ \begin{aligned} \frac{{{{\rm d}^2}y}}{{{\rm d}{\tau ^2}}} + & \frac{{2\zeta }}{\eta }\left| {\frac{{{\rm d}y}}{{{\rm {\rm d}}\tau }} + \frac{1}{{0.5H}}\frac{{{\rm d}f}}{{d\tau }}} \right|(\frac{{{\rm d}y}}{{{\rm d}\tau }} + \frac{1}{{0.5H}}\frac{{df}}{{{\rm d}\tau }}) + \\ & \frac{1}{{{\eta ^2}}}y + \frac{{{{\rm d}^2}f}}{{0.5Hd{\tau ^2}}} = \frac{1}{{{\eta ^2}}}{y_s}\;\;\;\;\;\;y > 0\text{;} \end{aligned} $ | (2) |
| $ \begin{aligned} \frac{{{{\rm d}^2}y}}{{{\rm d}{\tau ^2}}} + & \frac{{2\zeta }}{\eta }\left| {\frac{{{\rm d}y}}{{{\rm d}\tau }} + \frac{1}{{0.5H}}\frac{{{\rm d}f}}{{{\rm d}\tau }}} \right|(\frac{{dy}}{{{\rm d}\tau }} + \frac{1}{{0.5H}}\frac{{{\rm d}f}}{{{\rm d}\tau }}) + \\ & \frac{{{{\rm d}^2}f}}{{0.5H{\rm d}{\tau ^2}}} = \frac{1}{{{\eta ^2}}}{y_s}\;\;\;\;\;\;y \leqslant 0 \text{。} \end{aligned} $ | (3) |
式中:ζ为阻尼比,数值越大流体阻力越大;η为激励圆频率与固有圆频率之比;ys为在静止状态下缆索的伸长量与波幅的比值。
2 随机波浪数值模拟母船在波浪中运动,海浪运动具有随机性,可以看作平稳随机过程,由若干具有随机波幅、周期、相位的单元波叠加得到,可表示为:
| $ f(t) = \sum\limits_{i = 1}^\infty {{a_i}\cos ({\omega _i}t + {\varepsilon _i})} \text{。} $ | (4) |
式中:ai和wi分别为第i个单元谐波的波幅和圆频率;εi为第i个谐波的初相位,是均匀分布于0~2 π的随机变量。当单元谐波的频率增量Δω无限小时,单元谐波波幅可由海浪谱密度得出:
| $ {a_i} = \sqrt {2S({\varpi _i})\Delta {\omega _i}} \text{。} $ | (5) |
其中S(ω)为海浪谱密度函数。根据长期的观测和理论研究,海浪谱密度有多种表达形式,本文采用双参数PM波谱,包含了波高和周期2个波浪参数,谱密度函数为:
| $ S(\omega ) = \frac{{173H_{1/3}^2}}{{{\omega ^5}T_p^4}}\exp \left( {-\frac{{691}}{{{\omega ^4}T_p^4}}} \right)\text{。} $ | (6) |
式中:S(ω)为谱密度函数;H1/3为1/3有义波高;Tp为波浪特征周期。
为便于分析计算,需要对随机波浪进行无因次化,单元谐波的频率用与特征频率的比值来表示为:
| $ {\omega _i} = {k_i}\frac{{2{\rm{\pi }}}}{{{T_P}}}。 $ | (7) |
代入随机波浪表达式中,将式(4)和式(6)式合并到一起,并将时间变量改为无因次的τ得到无因次的波浪函数:
| $ \bar f = \frac{f}{{0.5H}} = \sum\limits_{i = 1}^\infty {\sqrt {\frac{{173}}{{2k_i^5{{\rm{\pi }}^4}}}\exp \left( {\frac{{ - 691}}{{{{(2{\rm{\pi }})}^4}k_i^4}}} \right)\Delta \eta } \cos ({k_i}\tau + {\varepsilon _i})} 。 $ | (8) |
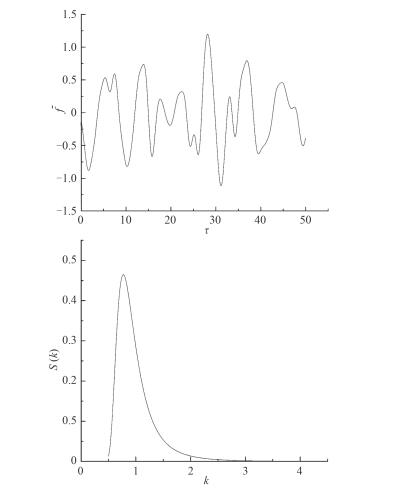
通过数值仿真可以得到时域历程图(见图 2)以及谱密度函数。
|
图 2 无因次随机波浪时域历程图和波浪谱 Fig. 2 Time history of non-dimensional random wave and wave spectrum |
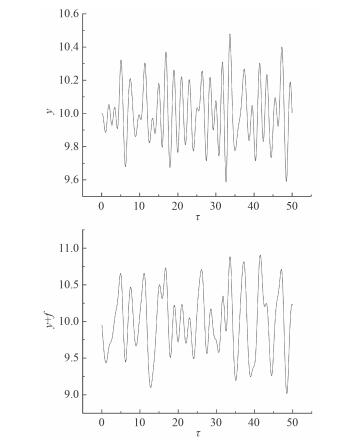
运动方程为强非线性微分方程,无法通过解析方法求解,因此采用龙格库塔法进行求解。方程(2)与方程(3)中3个系数ζ,η和ys分别为无因次的阻尼系数,频率比及初始相对伸长量。ζ=0.1,η=0.3,ys=10时的缆索伸缩量及ROV相对位移的时域历程图如图 3所示,此时缆索的刚度相对较小,缆索的伸长量相对波幅很大,可以看出始终处于张紧的状态。并且ROV的振幅大约为1,与激励幅值十分接近。
|
图 3 ζ=0.1,η=0.3,ys=10时,缆索伸缩量和ROV位移时域历程图 Fig. 3 Time history of cable's tension and ROV's displacement(ζ=0.1, η=0.3, ys=10) |
图 4为ys=1和ys=4时,不同的阻尼比和频率比下缆索张力的最大值与最小值的计算结果

|
图 4 ys=1和ys=4时,随机激励下缆索最大、最小张力与阻尼比、频率比的关系 Fig. 4 Tension of cable under random excitation for various η and ζ with ys=1 and ys=4 |
可以看出,其他参数相同的情况下,阻尼越小,ROV响应幅值越大;缆索初始伸长量越大,离松弛状态越远,缆索相对更加安全。从频率比上看,最大张力出现了多个峰值,其中在η=1处有一固定峰值,出现与谐波激励类似的共振现象;在η=3处附近有另外一个峰值,且随着ys的增大出现该峰值的频率有所后移。在η接近10时,ymax运动方程(2)和方程(3)中的激励项f取为谐波激励f=acos(wt),并用数值仿真得到的ys=1和ys=4的频域计算结果如图 5所示。

|
图 5 ys=1和ys=4时,谐波激励下缆索最大、最小张力与阻尼比、频率比的关系 Fig. 5 Tension of cable under harmonic excitation for various η and ζ with ys=1 and ys=4 |
谐波激励下,缆索最大伸缩量的幅值在η大于2之后下降较快,而随机波浪下,要在η接近于10时才会明显下降。此外谐波激励下尽在ys较小时ymax有多个峰值,张力大的频域范围相比随机波浪时小得多。
4 结语通过建立一维ROV作业系统的运动方程,考虑随机波浪以及非线性流体阻力的作用,并对方程以及随机波无因次化,利用数值仿真对缆索张力的变化进行仿真,并与谐波激励下的仿真结果作对比,结果表明:
1)缆索的最大张力随阻尼的增大而减小,在随机波浪作用下,频域内最大张力有多个峰值,其中不管缆索多长,在固有频率附近的峰值十分明显;频率较大时,由于随机波浪中包含了不同频率的谐波成分,共同作用下,在很大的频率范围内最大张力保持较大的数值。
2)相比谐波激励,随机激励下缆索的最大张力在频域的分布更为分散,虽然峰值较小,但不安全的频率范围大得多,因此在真实海浪中作业时,为避开缆索张力大的频率增加了难度,为ROV作业系统设置补偿系统减小张力十分必要。
| [1] | 俞聿修. 随机波浪及其工程应用[M]. 大连: 大连理工大学出版社, 2000 . |
| [2] |
胡海岩. 分段线性系统动力学的非光滑分析[J]. 力学学报 , 1996, 28 (4) :483–488.
HU Hai-yan. Nonsmooth analysis of dynamics of a piecewise linear system[J]. Chinese Journal of Theoretical and Applied Mechani , 1996, 28 (4) :483–488. |
| [3] | VASSALOS D, HUANG S. Dynamics of small-sagged taut-slack marine cables[J]. Computers & Structures , 1996, 58 (3) :557–562. |
| [4] | TJAVARAS A A, ZHU Q, LIU Y, et al. The mechanics of highly-extensible cables[J]. Journal of Sound and Vibration , 1998, 213 (4) :709–737. DOI:10.1006/jsvi.1998.1526 |
| [5] | NIEDZWECKI J M, THAMPI S K. Snap loading of marine cable systems[J]. Applied Ocean Research , 1991, 13 (1) :2–11. DOI:10.1016/S0141-1187(05)80035-5 |
| [6] | KOH C G, ZHANG Y, QUEK S T. Low-tension cable dynamics: Numerical and experimental studies[J]. Journal of Engineering Mechanics , 1999, 125 (3) :347–354. DOI:10.1061/(ASCE)0733-9399(1999)125:3(347) |
| [7] | DRISCOLL F R, LUECK R G, NAHON M. Development and validation of a lumped-mass dynamics model of a deep-sea ROV System[J]. Applied Ocean Research , 2000, 22 (3) :169–182. DOI:10.1016/S0141-1187(00)00002-X |
| [8] | HENNESSEY C M, PEARSON N J, PLAUT R H. Experimental snap loading of synthetic ropes[J]. Shock and Vibration , 2005, 12 (3) :163–175. DOI:10.1155/2005/734345 |
 2016, Vol. 38
2016, Vol. 38
