汽力装置回汽制动的原理是在正车汽轮机功率较大且舰体速度相对不高时,通过倒车汽轮机的进汽并产生回汽负载,在回汽负载与螺旋桨负载共同作用下,促使正车汽轮机迅速减速至指定转速[1]。回汽制动过程中,由于动力装置倒车汽轮机运行状态变化很大,极可能出现因为变工况速率过大而引起运行参数超限,导致倒车级动叶断裂的问题。
1 回汽制动工况下倒车汽轮机变工况工作过程分析回汽制动工况下,在接到制动指令后,倒车汽轮机进汽阀瞬间全部打开,倒车汽轮机进汽量瞬间增加至最大值,此后保持最大进汽状态。
在倒车进汽阀打开的瞬间,蒸汽经喷嘴、迎着倒车汽轮机动叶运动的方向进入倒车汽轮机动叶栅,产生阻止动叶运动的力,先期用于克服转子与轴系的惯性,促使转子尽快降速;在舰体航速降低、螺旋桨进入水轮机状态后,流过动叶栅的蒸汽将与轴系、主减速齿轮装置和正倒车汽轮机的各轴承一道,消耗螺旋桨产生的水轮机功率,改变拖带特性,增加螺旋桨的制动能力,在使螺旋桨尽快降低转速的同时,降低舰体航速;后期,当舰体航速下降、在螺旋桨上产生的水轮机功率不足以带动汽轮机转子和轴系继续旋转并同时克服蒸汽在倒车汽轮机动叶上产生的制动力之后,倒车汽轮机便处于锁制螺旋桨状态,螺旋桨停止转动;最后,当蒸汽在倒车汽轮机转子上产生的转矩大于螺旋桨上产生的水轮机转矩以及主汽轮机至轴系各转动部件的静摩擦转矩之和后,轴系开始按倒车方向加速旋转,直至舰体停止运动。
回汽制动过程中,由于汽轮机在回汽制动时的转速远高于全速倒车的转速,且从喷嘴流出的高速蒸汽又是迎着动叶运动的方向进入动叶栅,因而在动叶上产生的力和弯矩将大于全速倒车时的力和弯矩,可能导致倒车汽轮机动叶弯曲应力超过安全许用值,影响蒸汽动力装置的安全运行。
2 回汽制动工况下倒车级动叶弯曲应力模型叶片是实现蒸汽能量转换的主要部件,它所承受的负荷很重。在叶片进行能量转换时,叶片各截面因蒸汽力的弯曲作用而产生弯曲应力[2]。在正常做功工况下,汽轮机各级动叶的弯曲应力,在它的总应力中所占的比例不大。但当为了主汽轮机的迅速变向,用高参数蒸汽回汽制动汽力装置时,倒车级动叶的弯曲应力将会显著增大许多倍,以致达到倒车级动叶的抗弯强度。
2.1 回汽制动工况下倒车级受力模型倒车汽轮机正常做功及回汽制动工况下,喷嘴出口蒸汽流在弯曲的动叶栅通道内流动时,都会对动叶片产生冲击力,该力可分解为轴向和圆周方向两个分力。轴向分力是汽流作用在转子上的轴向力。圆周分力在正常做功工况下推动转子旋转做功,而在回汽制动工况下阻碍转子旋转。所以2种工况下,汽流作用在动叶上的力的性质不同。按照叶轮机械原理,用速度三角形法,可得回汽制动工况下,倒车汽轮机第一级实际耗功的单只动叶所承受的圆周力、轴向力及合力分别为[3]:
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{scus1}} = - \frac{{{D_{dc}}}}{{2{n_{dy1}}}}({C_{21sc}}^\prime \cos {\alpha _{21}}^\prime + {C_{11sc}}\cos {\alpha _{11}}),}\\ {{F_{scas1}} = \frac{{{D_{dc}}}}{{2{n_{dy1}}}}({C_{11sc}}\sin {\alpha _{11}} - {C_{21sc}}^\prime sin{\alpha _{21}}^\prime ),}\\ {{F_{bscs1}} = \sqrt {{F_{scus1}}^2 + {F_{scas1}}^2} .} \end{array}} \right. $ | (1) |
式中:Fscus1、Fscas1和Fbscs1分别为回汽制动工况下,倒车汽轮机第一级动叶栅单只叶片承受的圆周力、轴向力及合力;Ddc为倒车调节阀蒸汽流量;
倒车汽轮机第二级单只动叶受力与第一级动叶类似,这里不再赘述。
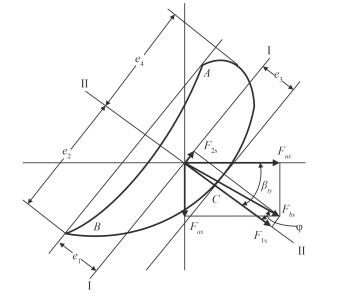
2.2 倒车级动叶的最大弯曲应力模型图 1是汽轮机单只动叶基面的受力分析图,通过截面重心取相互垂直的最小惯性轴线Ⅰ-Ⅰ和最大惯性轴线Ⅱ-Ⅱ,其中Ⅰ-Ⅰ轴平行于叶片进、出口边联线AB[4]。
|
图 1 汽轮机动叶基面的受力分析图 Fig. 1 Stress analysis diagram of basal plane for moving blade |
图 1中,蒸汽作用力Fbs投影到圆周方向、轴向方向的分力分别为Fus和Fas,投影到2个主惯性轴的分力F1s,F2s可分别表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{1s}} = {F_{bs}}\cos \varphi } \text{,}\\ {{F_{2s}} = {F_{bs}}\sin \varphi } \text{,}\\ {\varphi = {\beta _{ty}}-\arctan \frac{{{F_{as}}}}{{{F_{us}}}}} \text{。} \end{array}} \right. $ | (2) |
式中:φ为Fbs与Ⅱ-Ⅱ轴的夹角;βty为Ⅱ-Ⅱ轴与圆周方向的夹角。
根据式(2)可得F1s和F2s对应于根部截面以Ⅰ-Ⅰ轴和Ⅱ-Ⅱ轴为中性轴的弯矩分别为[5]:
| $ \left\{ {\begin{array}{*{20}{c}} {{M_{1s}} = \frac{1}{2}{F_{1s}}{l_{dy}} = \frac{1}{2}{F_{bs}}{l_{dy}}\cos \varphi ,}\\ {{M_{2s}} = \frac{1}{2}{F_{2s}}{l_{dy}} = \frac{1}{2}{F_{bs}}{l_{dy}}\sin \varphi .} \end{array}} \right. $ | (3) |
式中:M1s为F1s对叶型截面的最小主惯性轴(Ⅰ-Ⅰ轴)的弯矩;M2s为F2s对叶型截面的最大主惯性轴(Ⅱ-Ⅱ轴)的弯矩,
由图 1可看出,相对于Ⅰ-Ⅰ轴与Ⅱ-Ⅱ轴,最大弯曲应力发生在A,B,C点。因此,M1s及M2s作用在进、出汽边及背弧上的最大弯曲应力分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{As}} = \frac{{{F_{bs}}{l_{dy}}{e_1}\cos \varphi }}{{2{I_{\rm{I}}} \times {{10}^6}}} - \frac{{{F_{bs}}{l_{dy}}{e_4}\cos \varphi }}{{2{I_{{\rm{II}}}} \times {{10}^6}}},}\\ {{\sigma _{Bs}} = \frac{{{F_{bs}}{l_{dy}}{e_1}\cos \varphi }}{{2{I_{\rm{I}}} \times {{10}^6}}} + \frac{{{F_{bs}}{l_{dy}}{e_1}\cos \varphi }}{{2{I_{{\rm{II}}}} \times {{10}^6}}},}\\ {{\sigma _{Cs}} = - \frac{{{F_{bs}}{l_{dy}}{e_3}\cos \varphi }}{{2{I_{\rm{I}}} \times {{10}^6}}}.} \end{array}} \right. $ | (4) |
式中:σAs,σBs和σCs分别为M1s及M2s作用在进汽边、出汽边及背弧的应力;II和III分别为叶型最小主惯性轴Ⅰ-Ⅰ轴和最大主惯性轴Ⅱ-Ⅱ轴的惯性矩;e1为Ⅰ-Ⅰ轴与进、出口边联线AB的水平距离;e2为B点到Ⅱ-Ⅱ轴的距离;e3为C点到Ⅰ-Ⅰ轴的距离;e4为蒸汽入口到Ⅱ-Ⅱ轴的距离。
对于倒车汽轮机动叶片来说,Fbs与Ⅱ-Ⅱ轴的夹角φ很小,可近似认为等于0,按此方法计算得出的弯曲应力偏大,更安全。则式(4)可进一步简化为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{As}} = {\sigma _{Bs}} = \frac{{{F_{bs}}{l_{dy}}{e_1}}}{{2{I_{\rm{I}}} \times {{10}^6}}},}\\ {{\sigma _{Cs}} = - \frac{{{F_{bs}}{l_{dy}}{e_3}}}{{2{I_{\rm{I}}} \times {{10}^6}}}.} \end{array}} \right. $ | (5) |
由于动叶出口边缘点B离形心距离最远,该处的弯曲应力最大,从强度方面考虑,回汽制动过程中该处应力应为动叶上最大弯应力为[6]:
| $ {{\sigma _{\max }} = \frac{{{F_{bs}}{l_{dy}}{e_1}}}{{2{I_{\text{I}}} \times {{10}^6}}}}\text{。} $ | (6) |
式中:σmax为动叶上最大弯应力;II为叶型最小主惯性轴Ⅰ-Ⅰ轴的惯性矩;e1为Ⅰ-Ⅰ轴与进、出口边联线的水平距离;ldy为倒车汽轮机动叶叶高。
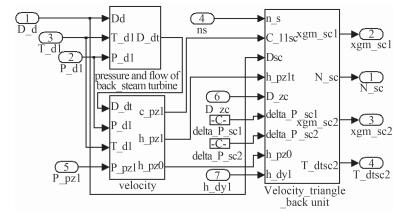
3 仿真模型 3.1 倒车级动叶最大弯曲应力的Simulink仿真模型在构建上述回汽制动工况下倒车级动叶的最大弯曲应力数学模型后,本文采用Matlab/Simulink仿真工具箱建立其仿真模型,用于实现汽力装置回汽制动工况下,倒车级动叶上最大弯曲应力的仿真计算,其详细框图如图 1所示。通过输入正车进汽量、倒车进汽量、倒车阀出口蒸汽压力及温度等变量参数随时间变化曲线,计算输出汽流对倒车级第一级及第二级动叶片产生的最大弯曲应力随时间变化曲线。
|
图 1 回汽制动工况下倒车级动叶弯曲应力的仿真模型 Fig. 1 Simulation model of bending stress of moving blade of the astern turbines in the Back-steam braking condition |
建立仿真模型,给定仿真环境为汽力装置采用理想回汽制动策略,即船舶在接到制动指令的瞬间,正车汽轮机迅速停止供汽,倒车汽轮机迅速打开进汽阀以全参数蒸汽回汽制动。本节依据正、倒车进汽量以及蒸汽状态参数,分析回汽制动工况下,各倒车级动叶最大弯曲应力随时间的变化曲线。
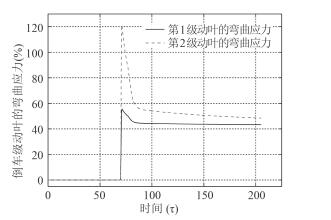
图 2给出了理想回汽制动策略下,倒车级两级动叶的最大弯曲应力随时间变化曲线。从图中可看出,理想制动策略下,主机以正车全速惰转用倒车全参数蒸汽回汽制动瞬间时,倒车汽轮机两级叶片的弯曲应力会骤增,第1级和第2级动叶的弯曲应力分别变为56.66%、126.98%。且第2级动叶弯曲应力增加的倍数比第1级动叶大,第1级动叶的弯曲应力增大为全速倒车工况的1.32倍,第2级动叶的弯曲应力增大为全速倒车工况的2.78倍。随后,伴随回汽制动负载转矩的作用,倒车汽轮机转速随之降低,动叶弯曲应力也降低。
|
图 2 倒车级两级动叶最大弯曲应力随时间变化曲线 Fig. 2 Change curve of maximum bending stress of the double moving blade according to the time |
因此,理想制动策略下,倒车级第1级动叶的弯曲应力在许用范围内,而倒车级第2级动叶的最大弯曲应力为126.98%,超过倒车级动叶许用弯曲应力,会影响倒车汽轮机的安全运行。
4 结语通过对回汽制动工况下,蒸汽动力装置的运行状态分析,建立了回汽制动工况下倒车级两级动叶的弯曲应力数学模型及其仿真模型,分析倒车汽轮机在回汽制动工况下的安全性能。
仿真结果表明,回汽制动工况下,采用理想制动策略时,倒车级第2级动叶弯曲应力可能超过安全许用值,影响汽力装置的安全运行。因此,在实际回汽制动过程中,应在理想回汽制动策略的基础上,适当减缓倒车汽轮机进汽阀开启的时机及幅度。
| [1] |
朱泳, 金家善, 刘东东. 舰用蒸汽动力装置回汽刹车与回汽保护技术研究[J]. 汽轮机技术 , 2012, 54 (6) :404–407.
ZHU Yong, JIN Jia-shan, LIU Dong-dong. Study of back-steam braking and back-steam protection technology for marine steam power plants[J]. Turbine Technology , 2012, 54 (6) :404–407. |
| [2] | BASSEL W S, GOMES A V. A metastable wet steam turbine stage model[J]. Nuclear Engineering and Design , 2002, 216 (1/3) :113–119. |
| [3] |
朱泳, 金家善, 刘东东. 蒸汽动力舰船回汽制动机理与系统建模仿真[J]. 中南大学学报(自然科学版) , 2013, 44 (7) :2771–2777.
ZHU Yong, JIN Jia-shan, LIU Dong-dong. Numerical modeling and mechanism of back-steam braking for steam-powered ships[J]. Journal of Central South University (science and technology) , 2013, 44 (7) :2771–2777. |
| [4] | 于瑞侠. 核动力汽轮机[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000 : 50 . |
| [5] | 张俊迈, 胡德明. 舰船汽轮机[M]. 北京: 国防工业出版社, 1988 : 112 -115. |
| [6] | SHANKAR P V G. Simulation model of a nuclear reactor turbine[J]. Nuclear Engineering and Design , 1977, 44 (2) :269–277. DOI:10.1016/0029-5493(77)90034-6 |
 2016, Vol. 38
2016, Vol. 38
