螺旋桨是舰船的主要推进装置,由于它直接在水中运转,产生的噪声在船体外形成,并直接辐射到海水中。近年来,国内外对无空泡状态下螺旋桨噪声的辐射特性和频率特性等开展了大量的理论研究和试验研究[1-3],对螺旋桨噪声的产生机理有了一定的认识[4]。但由于影响螺旋桨噪声的因素很多,采用试验和理论预报方法都存在一定的不足,目前随着CFD技术的发展使得用数值方法处理螺旋桨噪声问题成为可能[5-10]。本文采用LES方法计算分析螺旋桨近场脉动压力分布特性,并结合FW-H声比拟理论将声场计算和流场计算结合在一起,计算分析螺旋桨无空泡噪声。
1 数值方法 1.1 计算方法Lighthill将流体运动发声的复杂现象用静态介质中存在等效声源的声学问题来进行类比,认为流噪声是由速度波动、熵波动、粘性应力的非线性相互作用而产生的流动非稳定引起。Lighthill方程为:
| $ c_0^2{\nabla ^2}{\rho ^{'}}-\frac{{{\partial ^2}{\rho ^{'}}}}{{{\partial ^2}{t^2}}} = -\frac{{\partial Q}}{{\partial t}} + \nabla \cdot \vec F-\frac{{{\partial ^2}{T_{ij}}}}{{\partial {x_i}\partial {y_j}}}\text{,} $ | (1) |
| $ {T_{ij}} = \rho {U_i}{U_j} + {\delta _{ij}}(p-c_0^2{\rho ^{'}})-{\tau _{ij}}\text{。} $ | (2) |
式中:
| $ c_0^2{\nabla ^2}{\rho ^{'}}-\frac{{{\partial ^2}{\rho ^{'}}}}{{{\partial ^2}{t^2}}} = -\left[{\frac{{\partial Q}}{{\partial t}}-\nabla \cdot \vec F + \frac{{{\partial ^2}({\rho _0}{U_i}{U_j})}}{{\partial {x_i}{x_j}}}} \right]\text{。} $ | (3) |
Lighthill方程为自由空间假设下得到,FW-H方程考虑了流体中包含任意运动表面的情况:
| $ \begin{array}{l} c_0^2{{\bar \nabla }^2}{\rho ^{'}}-\displaystyle\frac{{{{\bar \partial }^2}{\rho ^{'}}}}{{{\partial ^2}{t^2}}} = -\displaystyle\frac{{\bar \partial }}{{\partial t}}\left\{ {{\rho _0}{\nu _n}\left| {\nabla f} \right|\delta (f)} \right\} + \\[10pt] \quad \quad \quad \quad \!\!\displaystyle\frac{{\bar \partial }}{{\partial {x_i}}}\left\{ {{L_i}\left| {\nabla f} \right|\delta (f)} \right\}-\frac{{{{\bar \partial }^2}{T_{ij}}}}{{\partial {x_i}\partial {x_j}}}\text{,} \end{array} $ | (4) |
| $ {L_i} = {p{'}_{ij}} \cdot {n_j} = {p{'}_{ij}}\frac{{\partial f/\partial {x_j}}}{{\left| {\nabla f} \right|}}\text{。} $ | (5) |
FW-H方程包含以下3部分噪声源:分布在表面以外的密度为Tij的四极子源;分布在表面上密度为Li的偶极子源;分布在表面上密度为ρ0νn的单极子源。
1.2 计算对象本文的计算对象为INSEAN E1619型7叶螺旋桨,直径D=0.35 m。计算中将螺旋桨置于与其同轴线的圆柱形流场区域中,进流面取为上游3 D,出流面取为下游7 D,径向取为5 D,如图 1所示。计算采用非结构网格,在螺旋桨叶片表面及旋转区域网格分布较密,在外部静止区域网格分布较稀疏,整个计算域的网格数约为200万。
|
图 1 螺旋桨计算域示意图 Fig. 1 Schematic of the propeller computational domain |
首先采用Fluent定常计算模块,采用Fluent提供的旋转坐标系计算均匀来流情况下螺旋桨的定常性能;待定常计算稳定后,采用k-ε湍流模型结合滑移网格计算非定常流场,得到周期性的流场结果;以此作为LES计算的初场,计算桨的非定常流场;待计算稳定后,启动Fluent声学计算模块,采用FW-H方法计算螺旋桨的水动力噪声。计算中空间离散格式和时间离散格式均采用2阶精度。
计算中取来流速度为3 m/s,桨叶转速为600 r/min,对应的叶频为70 Hz,时间步长dt=5 × 10-4s。待LES计算结果收敛稳定后,继续运行2 000步,运用FW-H方程计算远场辐射噪声,根据声学相关理论,此时得到的声场频率分辨率为1 Hz,能够得到的最高频率为1 000 Hz。本文螺旋桨噪声计算时选取桨叶表面的偶极子声源计算远场辐射噪声。
计算中的边界条件设置如下:入口及计算域周向设置为速度入口,速度方向平行于桨轴,为x轴方向;出口设置为压力出口;螺旋桨、桨毂、桨轴表面均设置为无滑移壁面条件。
2 计算结果及分析 2.1 近场脉动压力频率特性分析图 2为桨盘面脉动压力均方根分布,脉动压力在叶梢处较大,螺旋桨近场脉动压力主要来自于桨叶叶梢的速度扰动。为了进一步分析螺旋桨近场脉动压力频率特性,在螺旋桨近场设置20个脉动压力监测点,记录LES计算得到的时域压力信号,这20个监测点的位置如表 1所示。

|
图 2 桨盘面脉动压力均方根分布云图 Fig. 2 RMS of fluctuating pressure in the disk plane |
|
|
表 1 近场监测点位置 Tab.1 Location of near-field fluctuating pressure monitor |
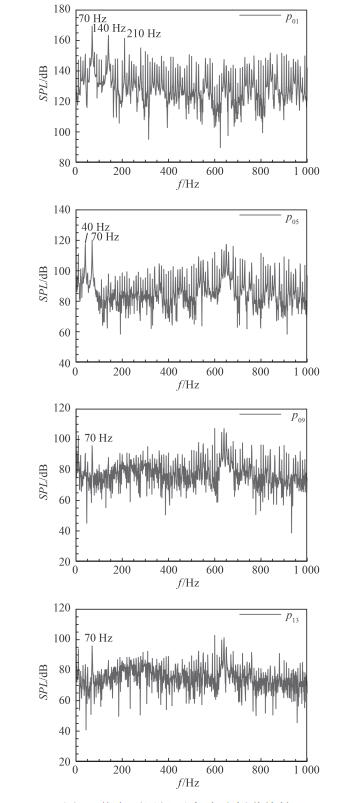
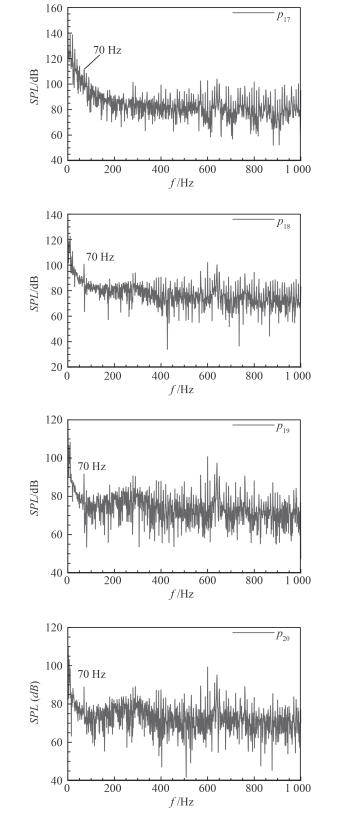
参考值取10-6 Pa,得到脉动监测点压力随频率的分布。从图 3中桨盘面p01,p05,p09,p13监测点的脉动压力分布情况对比可知,桨盘面压力在叶频(70 Hz)及其倍频处存在强线谱;叶梢处叶频特征明显,随着距离桨盘面中心径向距离增大,脉动压力叶频强线谱特征减弱,600 Hz附近出现了强线谱。图 4中,从桨轴方向p17,p18,p19,p20监测点的脉动压力分布情况对比可知,桨轴方向脉动压力频谱主要由轴频和600 Hz附近线谱占主导,叶频线谱特征不明显。因此,近场脉动压力在桨盘面和桨轴方向频谱特性存在差异,这可能是近场螺旋桨线谱噪声具有指向性的原因[6]。以上分析结果证实,脉动压力主要来自于湍流小扰动,在湍流区内以其低频分量为主,在湍流区外由低、高频分量占主导。
|
图 3 桨盘面近场压力脉动频谱特性 Fig. 3 Frequency characteristic of near-field fluctuating pressure in the disk plane |
|
图 4 桨轴方向近场压力脉动频谱特性 Fig. 4 Frequency characteristic of near-field fluctuating pressure in the axis plane |
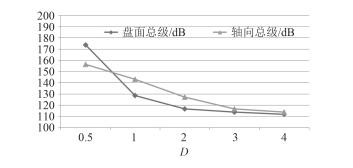
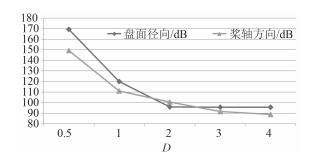
脉动压力起因于湍流速度扰动引起的动量脉动,它直接平衡与动量起伏。图 5和图 6进一步给出了脉动压力总级(1~1 000 Hz)和一阶叶频线谱幅值随着距离的变化关系。从图中可知,随着距离增大,轴向和盘面径向脉动压力总级、一阶叶频线谱幅值均随着距离增大迅速衰减。
|
图 5 脉动压力总级沿盘面径向和轴向分布 Fig. 5 Distribution of total fluctuating pressure in the radial and axis direction |
|
图 6 脉动压力一阶叶频幅值沿盘面径向和轴向分布 Fig. 6 Distribution of BPF fluctuating pressure in the radial and axis direction |
由于Fluent中FW-H方法只适用于求解紧致性声源的远场辐射噪声,对各声压接收点的结果转换到1 m处的声压总级并不相同,即各声压接收点得到的声压总级随距声源距离并不符合球面波衰减规律。为了得到声压总级随距声源距离的关系,在桨叶盘面径向每隔D取一个声压接收点,得到总声级随距离的分布关系。同时,由于远场辐射噪声随着距声源的距离符合球面波衰减规律,即距声源r处的总声级与1 m处的总声级满足:
| $ {\left( {SPL} \right)_r} = {\left( {SPL} \right)_{100 {\rm m}}}{\text{-}}20\log \left( {r/100} \right)\text{。} $ | (6) |
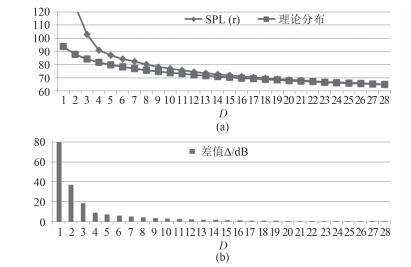
将100 m处的远场声压计算结果代入上述公式,得到总声级随距离的分布曲线,其与计算结果的对比如图 7(a)所示。从图中可知,距离声源较近时,声场接收点得到的声压较大,声压随距离并不符合球面波衰减的规律;随着距离的增大,声压计算值与理论值逐渐趋于一致,计算得到的声压总级基本符合理论的球面波衰减规律。图 7(b)进一步给出了声压总级计算与理论分布的差值随距离的变化关系,考虑到数值计算的误差,二者相差3 dB以内即可认为计算结果符合球面波衰减规律。从图中可知,此时声压接收点距离桨叶中心距离为10 D。因此,为了得到螺旋桨噪声的远场声辐射,声压监测点离声源的距离必要大于10倍的桨叶直径。
|
图 7 总声级随距离的变化情况 Fig. 7 Distribution of total sound pressure level with different distance |
在螺旋桨噪声的理论设计和工程应用中,需要得到全方位的噪声特性。因此,螺旋桨噪声的指向性研究对于开展低噪声螺旋桨设计以及衡量舰船噪声性能和进行水下目标识别都具有十分重要的意义[6]。为此,本文分别在桨盘面(YZ平面)和纵向平面(XY平面),距离转子中心r=30 D位置进行声场指向性研究。
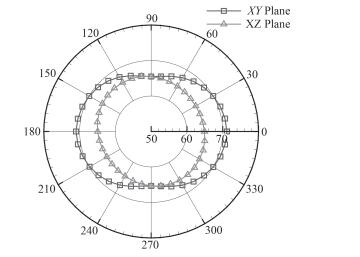
图 8为桨盘面和桨轴向平面总声压级(1~1 000 Hz)指向性图,在桨盘面,不同半径处总声压级虽然在周向存在一定的波动,但波动范围相对于平均值很小,总声压级在周向基本为定值。在纵向平面,螺旋桨远场噪声总级在轴向呈现椭圆形分布,轴向方向接收点的总声级比桨盘面高约6 dB。这是由于螺旋桨的远场声辐射主要来源于桨叶尾缘漩涡脱落引起的压力变化,由于螺旋桨尾涡沿着桨轴方向传播,因此桨轴方向的声辐射总级比桨盘面周向的大。
|
图 8 桨盘面和纵向平面噪声指向性分布 Fig. 8 Directivity of noise in disk plane and axis plane |
在螺旋桨远场设置8个声场接收点,记录FW-H计算得到的声场信号,这8个接收点的位置及计算得到的声压总级如表 2所示。桨盘面和桨轴方向总声级相差约5 dB。
|
|
表 2 远场声压接收点位置 Tab.2 Location of far fieled sound pressure receiver |
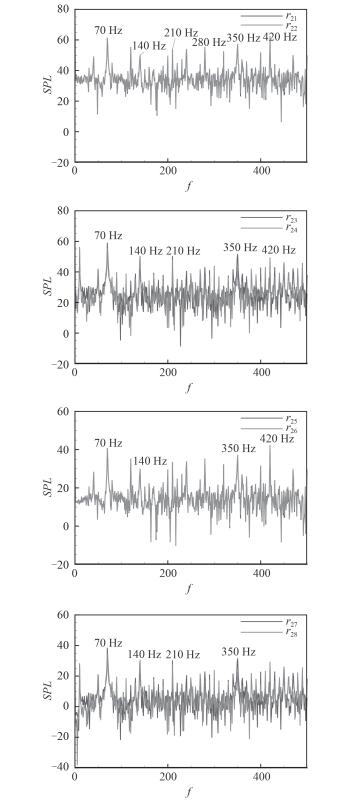
进一步分析远场声辐射的频率特性,图 9给出了采用Fluent中FW-H方法计算远场声压接收点的结果。从图中可知,所有的远场声压接收点在桨叶叶频及其倍频存在线谱,但仅桨叶盘面(点23、点24、点27、点28)接收点声压在轴频及其谐频处存在线谱。此外,r21,r22声压总级比r23,r24大,r25,r26声压总级比r27,r28大,与上一节的分析结论一致。因此,螺旋桨远场声辐射幅值不仅具有指向性,而且声辐射的频率特性在轴向和桨盘面也存在差异,在桨盘面声辐射轴频线谱突出,在轴向声辐射轴频线谱不明显。
|
图 9 远场声压频谱分布 Fig. 9 Distribution of far field sound pressure level with frequency |
本文采用LES方法结合FW-H声学模型计算分析了螺旋桨的近场脉动压力和远场声辐射特性。得到了以下结论:
1)螺旋桨近场脉动压力频率特性在桨盘面和桨轴方向存在差异,桨盘面叶频线谱突出,桨轴方向主要由轴频线谱占主导,随着距离增大,脉动压力迅速衰减;采用Fluent中FW-H方法计算辐射噪声时,声场接收点距声源距离必须大于10倍的桨叶直径。
2)螺旋桨远场声辐射的指向性分析表明,噪声总级在桨盘面轴向均匀分布,在纵向平面呈现椭圆形分布,桨轴方向声压比桨盘面声压大。进一步分析远场声辐射的频率特性发现,桨盘面声辐射轴频线谱突出,而桨轴方向声辐射轴频线谱不明显。
| [1] | 汤渭霖. 螺旋桨涡旋噪声预报[J]. 船舶力学 , 1999, 3 (2) :49–57. |
| [2] | 朱锡清, 吴武生. 螺旋桨负荷噪声研究[J]. 声学学报 , 1999, 24 (3) :259–268. |
| [3] | 朱锡清, 唐登海, 孙红星, 等. 船舶螺旋桨低频噪声研究[J]. 船舶力学 , 2000, 4 (1) :50–55. |
| [4] | 张永坤, 熊鹰, 赵小龙. 螺旋桨无空泡噪声预报[J]. 噪声振动与控制 , 2008, 28 (1) :44–47. |
| [5] | 王超.螺旋桨水动力性能、空泡及噪声性能的数值预报研究[D].哈尔滨:哈尔滨工程大学, 2010. http://www.oalib.com/references/18936664 |
| [6] | 谢剑波, 周其斗. 非均匀流场中螺旋桨线谱噪声指向性分析[J]. 中国舰船研究 , 2010, 5 (6) :6–11. |
| [7] | 杨琼方, 王永生, 曾文德, 等. 大侧斜螺旋桨负载噪声的边界元数值声学方法频域内计算分析[J]. 兵工学报 , 2011, 32 (9) :1118–1125. |
| [8] | 张漫.螺旋桨无空泡噪声的数值预报研究[D].大连:大连理工大学, 2013. http://cdmd.cnki.com.cn/article/cdmd-10141-1013198835.htm |
| [9] | SEOL H, JUNG B, SUH J C, et al. Prediction of non-cavitating underwater propeller noise[J]. Journal of Sound and Vibration , 2002, 257 (1) :131–156. DOI:10.1006/jsvi.2002.5035 |
| [10] | SEOL H, SUH J C, LEE S. Development of hybrid method for the prediction of underwater propeller noise[J]. Journal of Sound and Vibration , 2005, 288 (1/2) :345–360. |
| [11] | SCHRAM C, MARTÍNEZ-LERA P, TOURNOUR M. Two-dimensional in-duct vortex leapfrogging as a validation benchmark for internal aeroacoustics[C]//Proceedings of the 13th AIAA/CEAS aeroacoustics conference (28th AIAA Aeroacoustics Conference). Rome, Italy: AIAA, 2007. |
 2016, Vol. 38
2016, Vol. 38
