2. 哈尔滨工程大学, 黑龙江 哈尔滨 150001
2. Harbin Engineering University, Harbin 150001, China
潜艇的艇体、鱼雷等水下航行体外壳以及海洋平台的柱腿等结构大多可以简化为变截面加筋柱壳结构。在这些结构中,由于截面突变,使得它们往往是产生振动和辐射噪声的重要部分,且这些结构处于流场当中,其振动不能忽略流体的影响,因此对流场中变截面加筋柱壳结构的声振动特性进行研究具有重要的实际意义。
国内外关于圆柱壳结构的声振特性研究较多。通常采用能量法计算圆柱壳和肋骨的动能、应变能以及壳体表面声压、静水压力和激励力的势能,再运用哈密顿原理推导出系统的动力学方程[1],进行求解。也可以采用Flügge壳体理论和Helmholtz波动方程[2],计算圆柱壳体的声振特性。对于变截面柱壳结构声振特性分析通常采用能量法或幂级数展开的方法[3],并利用摄动法或波传播法[4]对变截面柱壳的振动和声辐射进行研究。但目前,针对船舶工程中复杂的变截面加筋柱壳结构的研究还不多见。
本文采用传递矩阵法给出变截面加筋柱壳结构在受集中力、声压作用下振动响应的求解过程,并探讨计算所取周向波数、声压系数、积分步长对计算精度的影响。在此基础上开展对结构振动特性的研究,分析结构损耗因子、流体介质、壳体厚度、环肋数目对变截面加筋柱壳结构声振特性的影响。
1 外界激励作用下的振动响应的求解流场对变截面加筋柱壳结构的作用即将声压Kmn(P)激励力中单项广义声压作为外激励力考虑进去,相对于考虑集中激励力单独作用的情况更加复杂,同时对于环肋或者变截面处的传递矩阵则可沿用文献[5]的处理方法,对于变厚度加筋柱壳结构流场压力的处理方式参考文献[6],对于锥壳-圆柱壳、环板-圆柱壳组合结构的流场作用参考文献[7]。外界激励作用下结构振动响应的求解过程如下:
1)将结构沿着母线方向分成N个分段。
2)对N个分段分别进行分析,若第j个分段之中没有环肋或截面突变,则满足:
| $ \left\{ \begin{array}{l} {T_{j + 1}} = \exp \left[ {\int_{{\xi _i}}^{{\xi _{j + 1}}} {U\left( \tau \right){\rm{d}}\tau } } \right],\\ {P_{j + 1}} = \int_{{\xi _j}}^{{\xi _{j + 1}}} {\exp \left[ {\int_\tau ^{{\xi _{j + 1}}} {U\left( s \right)ds} } \right]f\left( \tau \right){\rm{d}}\tau ,} \\ j = 1, \cdots ,n - 1. \end{array} \right. $ | (1) |
若第j个分段之中有环肋或者截面突变,则满足:
| $ \left\{ \begin{array}{l} {T_{j + 1}} = - \exp \left[ {\int_{{\xi _i}}^{{\xi _{j + 1}}} {\rm{U}}\left( \tau \right){\rm{d}}\tau } \right]T{r_i}\exp {\left[ {\int_{{\xi _j}}^{{\xi _i}} U\left( \tau \right){\rm{d}}\tau } \right]_i},\\ {P_{j + 1}} = \exp \left[ {\int_{{\xi _i}}^{{\xi _{j + 1}}} U\left( \tau \right)d\tau } \right]T{r_i}\exp \left[ {\int_\tau ^{{\xi _i}} U\left( s \right){\rm{d}}s} \right]f\left( \tau \right){\rm{d}}\tau + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{\xi _i}}^{{\xi _{j + 1}}} {\exp \left[ {\int_\tau ^{{\xi _{j + 1}}} {U\left( s \right){\rm{d}}s} } \right]f\left( \tau \right){\rm{d}}\tau .} \end{array} \right. $ | (2) |
式中:Tj + 1为第j分段的场传递矩阵;U为圆柱壳、锥壳或环板的系数矩阵,参见文献[4];Pj + 1为第j分段外载荷作用引起的非齐次项;
3)计算Tj + 1、Pj + 1,构造第j分段的传递关系:
| $ Z\left( {{\xi }_{j+1}} \right)={{T}_{j+1}}Z\left( {{\xi }_{j}} \right)+{{P}_{j+1}} $ |
| $ j=1,\cdots ,n $ |
对于Tj + 1的求解采用钟万勰[8]的精细算法进行处理。
对于Pj + 1的计算,可通过高斯积分法求解:
| $ \begin{aligned} \int_{{\xi _j}}^{{\xi _{j + 1}}} & {\exp \left[{\int_\tau ^{{\xi _{j + 1}}} {U\left( s \right){\rm d}s} } \right]} f\left( \tau \right){\rm d}\tau = \\ & \frac{{\Delta \xi }}{2}\sum\limits_{k = 1}^n {{A_k}\exp \left[{U\left( {\bar \xi } \right)\frac{{\Delta \xi }}{2}\left( {1-{x_k}} \right)} \right]}\times \\ & f\left( {{\xi _j} + \frac{{\Delta \xi }}{2}\left( {1 + {x_k}} \right)} \right) + o\left( {\Delta {\xi ^{2n}}} \right)\text{。} \end{aligned} $ | (3) |
式中,n为积分点的个数,xk为积分点的坐标,Ak为加权系数。
将式(3)代入第j分段的传递关系中可得:
| $ \begin{aligned} Z\left( {{\xi }_{j+1}} \right)\!=\! & {{T}_{j+1}}Z\left( {{\xi }_{j}} \right)\!+\!\!\sum\limits_{k=1}^{n}{{{A}_{k}}\exp \left[U\left( {\bar{\xi }} \right)\frac{\Delta \xi }{2}\left( 1\!-\!{{x}_{k}} \right) \right]} \times\\ & f\left( {{\xi }_{j}}+\frac{\Delta \xi }{2}\left( 1+{{x}_{k}} \right) \right)+o\left( \Delta {{\xi }^{2n}} \right) \text{。}\\ \end{aligned} $ | (4) |
4)借助于有限元封装刚度阵、质量阵的思想,将N段整合成总的方程组:
| $ {{\left[\begin{matrix} -{{T}_{2}} & \! \! \! \! \! \! \! I & {} & {} & {} & {} \\ {} & \! \! \! \! \! \! -{{T}_{3}} \! \! \! \! \! \! \! & I & {} & {} & {} \\ {} & {} & \! \! \! \! \! \! -{{T}_{4}} & \! \! \! \! \! \! I & {} & {} \\ {} & {} & {} & \! \! \! \! \! \! \cdots & \! \! \! \! \! \! I & {} \\ {} & {} & {} & {} & \! \! \! \! \! \! -{{T}_{n}} & \! \! \! \! \! \! I \\ \end{matrix} \right]}_{\left( 8n-8,8n \right)}}{{\left[\begin{matrix} Z\left( {{\xi }_{1}} \right) \\ Z\left( {{\xi }_{2}} \right) \\ Z\left( {{\xi }_{3}} \right) \\ \vdots \\ Z\left( {{\xi }_{n}} \right) \\ \end{matrix} \right]}_{\left( 8n,1 \right)}} \!\!\! = \! {{\left[\begin{matrix} {{P}_{2}} \\ {{P}_{3}} \\ {{P}_{4}} \\ \vdots \\ {{P}_{n}} \\ \end{matrix} \right]}_{\left( 8n-8,1 \right)}} $ | (5) |
根据两端的边界条件,删除系数矩阵中状态向量的值为0的列,通过求解方程可得到流场下结构各处的状态向量值。
2 流场辐射声压的求解根据叠加原理可知,变截面加筋柱壳结构表面各点在给定周向波数n下的法相位移为:
| $ {{w}_{n}}\left( P \right)=w_{n}^{f}\left( P \right)+\sum\limits_{m=-\infty }^{+\infty }{{{c}_{mn}}w_{mn}^{p}\left( P \right)},P\in {{S}_{2}}\text{。} $ | (6) |
对于壳体两端人为假定的刚性障板来说(刚性障板S1,S3与变截面组合壳表面S2一起组成封闭结构),满足
| $ {{w}_{n}}\left( P \right)=0,P\in {{S}_{2}}\cup {{S}_{3}}\text{。} $ | (7) |
在S2区域,以几何突变结构为例,存在关系:
| $ \begin{array}{*{20}{l}} {\sum\limits_{m = - \infty }^{ + \infty } {{c_{mn}}{{K'}_{mn}}\left( P \right)} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{c}} {0,P \in {S_1} \cup {S_3}}\\ {{\rho _0}{\omega ^2}\left( {w_n^f\left( P \right) + \sum\limits_{m = - \infty }^{ + \infty } {{c_{mm}}w_{mn}^p\left( P \right)} } \right),} \end{array}} \right.{\mkern 1mu} {\mkern 1mu} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P \in S_2^{,n \in \left( { - \infty , + \infty } \right)}} \end{array} $ | (8) |
给定周期定向波数n下,对于封闭系统表面任一点在均满足上式。故沿着封闭系统母线进行配点
| $ {{\left[U \right]}_{n}}{{\left\{ c \right\}}_{n}}={{\left\{ Q \right\}}_{n}},n\in \left( -\infty ,+\infty \right) $ | (9) |
式中
展开系数构成的列向量可知:
| $ {{\left[U \right]}_{q\times 2m+1}}\!\!=\!\!\left\{ \begin{aligned} & \left[{{{{K}'}}_{mn}}\left( {{P}_{sj}} \right) \right],P\!\in\! {{S}_{1}}\!\cup \!{{S}_{3}}\text{,} \\ & \left[{{{{K}'}}_{mn}}\left( {{P}_{sj}} \right)\!-\!{{\rho }_{0}}{{\omega }^{2}}w_{mn}^{p}\left( {{P}_{sj}} \right) \right],P\!\in \!{{S}_{2}} \text{。} \\ \end{aligned} \right. $ | (10) |
| $ {{\left[Q \right]}_{q\times 1}}=\left\{ \begin{aligned} & 0,P\in {{S}_{1}}\cup {{S}_{3}} \text{,} \\ & {{\rho }_{0}}{{\omega }^{2}}w_{m}^{f}\left( {{P}_{sj}} \right),P\in {{S}_{2}}\text{。} \\ \end{aligned} \right. $ | (11) |
由于该方程组为超静定方程组,故可用Moore-Penrose广义求逆法进行求解式中{c},将求得结果再代入式中可求出流场辐射声压。
3 模态的截断及算法有效性本文方法是基于模态展开来研究结构的声振性能的,而对壳体振动与声辐射起主导作用的仅是其中一部分模态,在确保计算精度的条件下,希望减小计算量,因此在求解结构的声振特性之前,首先需要对模态进行截断,即确定周向波数、声压系数、积分步长、配点数等。通过本文方法的计算结果与文献[1]中的理论计算结果和试验值进行对比,并综合考虑计算精度、效率和时间,取积分步长0.005 m、配点数61个、周向波数0~9、声压系数0~25比较合适,计算结果能满足精度要求。
4 变截面加筋柱壳结构声振特性分析1)损耗因子对振动和声辐射的影响
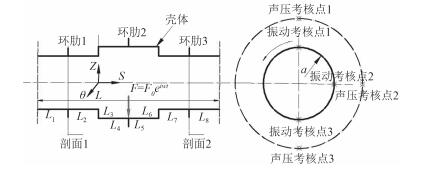
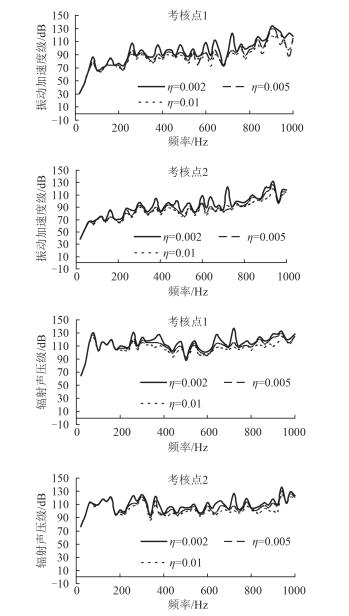
图 1所示为含有3道环肋的环板-圆柱壳组合柱壳结构简图。壳体材料选用钢,其结构质量密度ρ=7800 kg/m3,弹性模量E=20.6 × 104MPa,泊松比µ=0.3,流体介质密度ρw=1000 kg/m3,水中声速cw=1500 m/s。圆柱壳参数为:小圆柱段L1=L2=L7=L8=0.4 m,半径r=0.6m;大圆柱长L4=L5=0.4m,半径R=0.8m,圆柱壳和环板厚度均为0.002 m,3根外肋截面尺寸2 mm × 50 mm,结构在截面突变处受到单位谐激励力,采用前述传递矩阵法计算结构的振动与声辐射响应,计算的频率范围为20~1 000 Hz,研究结构损耗因子对声振特性的影响,分别取结构损耗因子为0.002,0.004,0.006,得到各考核点的振动加速度级或辐射声压级对比曲线如图 2所示。
|
图 1 环板-圆柱壳加筋柱壳结构以及考核点 Fig. 1 The ring plate-cylindrical shell stiffened cylindrical shell structure and check point |
|
图 2 不同损耗因子下结构的振动与声辐射响应曲线 Fig. 2 The curve of structure vibration and acoustic radiation under the different dissipation factor |
从图中可看出:1)结构阻尼损耗因子对变截面加筋柱壳结构声振特性有较大的影响,在200 Hz之前的低频段,损耗因子的影响较小,不同损耗因子下的振动和声辐射曲线基本吻合在一起;2)而在中高频段,随着损耗因子的增加,辐射声压和振动响应均整体降低,尤其在曲线的峰值点下降更多,曲线由陡峭变得平缓。
2)流体介质对振动和声辐射的影响
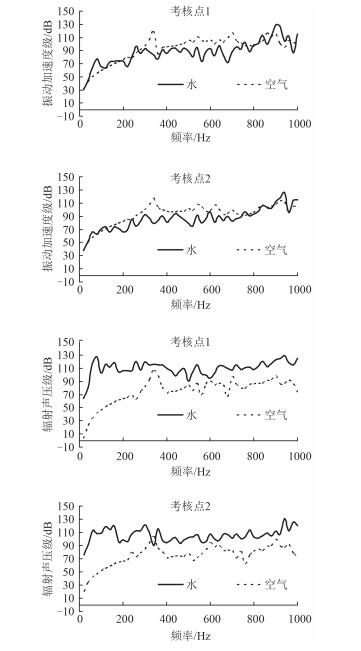
图 3给出了结构分别置于水和空气中对应的振动与声辐射对比曲线,由图可知:流体介质对结构的声振特性影响较大,这是因为流体介质的阻抗不同改变了流体与结构相互耦合的辐射阻抗值,进而改变了圆柱壳体的共振和声辐射特性。具体规律为:1)就振动特性而言,在频段内水中的振动小于空气中的振动,且振动峰值点被压平,曲线变平缓,可见重流体介质可以很好的抑制隔振峰值;2)对于结构声辐射,在空气中的辐射声压级明显小于水中声压,且在空气中曲线波动减少,波幅变大。
|
图 3 不同流体介质下结构的振动与声辐射响应曲线 Fig. 3 The curve of structure vibration and acoustic radiation under the different fluid medium |
3)壳体厚度对振动和声辐射的影响
图 4给出了柱壳壳体厚度分别为0.002 m,0.004 m,0.006 m所对应考核点的振动与声辐射对比曲线。由图可知:1)在低频段,随着壳体厚度增大,振动和声辐射均减小;2)随着频率升高,壳体厚度增大,结构的振动响应减小,但声辐射曲线出现交叉波动的特征。可见,壳体厚度增加引起的刚度增大,降低了结构的振动,同时改变了结构的声辐射频响规律。

|
图 4 不同壳体厚度下结构的振动与声辐射响应曲线 Fig. 4 The curve of structure vibration and acoustic radiation under the different shell thickness |
4)环肋数目对振动和声辐射的影响
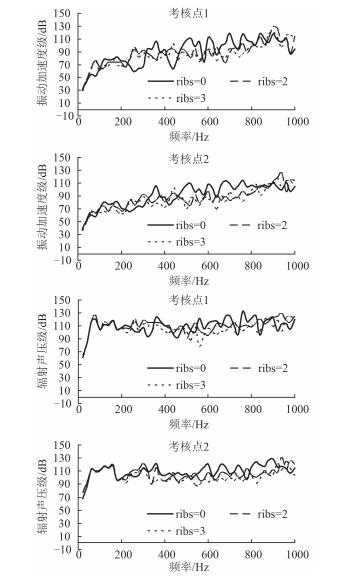
图 5给出了结构环肋数目为0、环肋数目2(保留环肋1、3)、环肋数目3所对应考核点的振动与声辐射对比曲线。通过对比分析可知:1)环肋的存在改变了柱壳结构的振动特性,使得加速度响应从低频段开始就发生较大差异,并引起加速度响应尖峰位置和高度的改变;2)随着环肋数目的增加,刚度增大,总体上来看加速度响应也有所减小;3)对于结构声辐射,在低于200 Hz的低频段环肋的数目对结构辐射声压的影响较小,在中高频段,随着环肋数目的增加,辐射声压级也有显著降低。
|
图 5 不同壳体厚度下结构的振动与声辐射响应曲线 Fig. 5 The curve of structure vibration and acoustic radiation under the different ring stiffeners number |
本文将流场对结构的声压作为外力考虑进来,基于传递矩阵法给出变截面加筋柱壳结构在受集中力、声压作用下振动与声辐射的求解过程,并通过算例计算确定周向波数、声压系数、积分步长等参数的选取。在此基础上开展对结构振动特性的研究,分析了环板-圆柱壳加筋柱壳结构的损耗因子、流体介质、壳体厚度、环肋数目对其声振特性的影响,主要结论如下:
1)损耗因子在低频段对结构的声振响应影响较小,而在中高频段,振动响应和辐射声压均随损耗因子增加整体降低,尤其是在振动响应的峰值点则下降更显著;
2)流体介质对结构的声振特性影响较大,就振动特性而言,在频段内水中的振动小于空气中的振动,且振动峰值点被压平,曲线变平缓,对于结构声辐射,在空气中的辐射声压级明显小于水中声压,且在空气中曲线波动减少,波幅变大。
3)壳体厚度增大能够减小壳体的振动响应,降低低频段结构的声辐射,同时使中高频段的声辐射曲线出现交叉波动的复杂特征。
4)环肋数目增加后,结构振动减小,而结构辐射声压在低频段无明显变化,但在中高频段,随着环肋数目的增加,辐射声压级也有显著降低。
| [1] |
谢官模.环肋圆柱壳在流场中的动力响应和声辐射[D].武汉:华中理工大学, 1994.
XIE Guan-mo. Dynamic response and acoustic radiation of a ring stiffened cylindrical shell in fluid field[D]. Wuhan: Huazhong University of Science and Technology, 1994. |
| [2] |
陈越澎, 骆东平, 陈晓宁, 等. 流场中双层壳体结构振动特性研究[J]. 华中理工大学学报 , 1999, 27 (1) :72–73.
CHEN Yue-peng, LUO Dong-ping, CHEN Xiao-ning, et al. A study of the characteristics of vibration in a double shell in a fluid field[J]. Journal of Huazhong University of Science and Technology , 1999, 27 (1) :72–73. |
| [3] |
曹雄涛, 华宏星. 流体作用下正交各向异性圆锥壳的自由振动[J]. 振动与冲击 , 2011, 30 (11) :95–100.
CAO Xiong-tao, HUA Hong-xing. Free vibration of orthotropic conical shell interacting with fluid[J]. Journal of Vibration and Shock , 2011, 30 (11) :95–100. |
| [4] | GUO Y P. Fluid-loading effects on waves on conical shells[J]. Journal of the Acoustical Society of America , 1995, 92 (2) :1061–1066. |
| [5] |
王宏, 刘贤贺, 徐伟. 变截面加筋柱壳结构振动特性分析[J]. 舰船科学技术 , 2015, 37 (8) :35–39.
WANG Hong, LIU Xian-he, XU Wei. Analysis of vibration characteristics of variable cross-section stiffened cylindrical shell[J]. Ship Science and Technology , 2015, 37 (8) :35–39. |
| [6] |
曹雷, 马运义, 黄玉盈. 基于Riccati传递矩阵法分析水下有限长环肋圆柱壳的声辐射性能[J]. 振动与冲击 , 2009, 28 (9) :149–154.
CAO Lei, MA Yun-yi, HUANG Yu-ying. Analysis of acoustic radiation of a ring-stiffened cylindrical shell with finite length in underwater based on Riccati transfer matrix method[J]. Journal of Vibration and Shock , 2009, 28 (9) :149–154. |
| [7] | KOOPMANN G H, SONG L M, FAHNLINE J B. A method for computing acoustic fields based on the principle of wave superposition[J]. Journal of the acoustical society of America , 1989, 86 (6) :2433–2438. DOI:10.1121/1.398450 |
| [8] |
钟万勰. 结构动力方程的精细时程积分法[J]. 大连理工大学学报 , 1994, 34 (2) :131–136.
ZHONG Wan-xie. On precise time-integration method for structural dynamics[J]. Journal of Dalian University of Technology , 1994, 34 (2) :131–136. |
 2016, Vol. 38
2016, Vol. 38
