近年来,船舶朝着大型化、快速化迅速发展,随着船舶吨位的增加,甲板面积的增大,船首外飘程度更大,由此带来的首部砰击问题更加严重。强烈的砰击对船舶的危害很大,一方面使冲击区域承受巨大的压力,局部结构屈曲甚至破坏;另一方面将引起整个船体剧烈的颤振,可能会导致船舶总纵强度或者局部强度的丧失[1]。
目前,关于船舶首部砰击的研究,多采用首部局部建模或者船首剖面建模,文献[2]采用的建立首部局部模型研究S175型船首部甲板上浪问题。文献[3]运用MSC.Dytran模拟船体二维剖面入水来计算船体底部砰击压力,没有涉及三维船体的计算。文献[4]建立了3种不同的船首部的局部模型,研究其入水时的砰击压力峰值。文献[5]建立了船首部剖面模型与船首部局部模型,对比了剖面垂直入水、船首部有航速与无航速入水3种情况的砰击压力峰值。文献[6]建立了Aarsnes[7]以及Arai & Matsunaga[8]进行的船体剖面试验中的模型,并对其采用SPH方法进行了入水砰击计算。文献[9]中对某大型集装箱船首部局部模型的外飘砰击压力进行了理论计算。以上文献都没有涉及全船计算模型的研究。
全船建模相比于船体剖面建模和船首部局部建模的优势在于能更准确地预报其船体运动响应,并可将预报结果直接作为砰击预报中的船体运动参数输入;其次,在仿真中可以附加船舶的纵摇运动,综合体现船体在波浪中纵摇与垂荡运动的耦合运动状态,更接近实船在波浪中的运动模式。故本文采用全船建模的方式对航速对船舶入水砰击的影响问题进行研究。
1 基本理论 1.1 拉格朗日有限元法MSC.Dytran是瞬态动力学流固耦合领域的高端软件,它的求解方法在时间域上采用显式时间积分法。设当前时间步是n,显式积分方法是将运动微分方程
| $ M{a_n} + C{v_n} + K{d_n} = F_n^{ext} $ | (1) |
改写成
| $ M{a_n} = F_n^{ext} - F_n^{int}, $ | (2) |
式中:Fnext为外载荷矢量;Fnint为内力矢量,Fnint=Cvn+Kdn。
加速度通过对质量矩阵求逆并乘以剩余力矢量
| $ {a_n} = {M^{ - 1}}F_n^{residual}. $ | (3) |
如果将单元质量分布在节点上,则为一对角阵,称为集中质量矩阵,线性方程组将成为一系列关于各个自由度的独立的一元一次方程,从而可求出节点加速度:
| $ {a_{ni}} = {F_{ni}}^{residual}/{M_i} $ | (4) |
如果假设加速度在一个时间步长内恒定,在时间推进上采用中心差分法:
| $ {v_{n + 1/2}} = {v_{n - 1/2}} + {a_n}(\Delta {t_{n + 1/2}} + \Delta {t_{n - 1/2}})/2, $ | (5) |
| $ {d_{n + 1}} = {d_n} + {v_{n + 1/2}}\Delta {t_{n + 1/2}}. $ | (6) |
显式积分法不需要做矩阵分解,因此具有很高的计算效率。
1.2 欧拉有限体积法初始条件已知情况下,利用控制方程求解每一欧拉单元在一个时间步的密度、速度、比内能和压力。假设tn时刻各物理参数已知,对相邻单元形心处流速进行线性插值求出单元边界处流速
| $ {u_b} = 1/2({u_1} + {u_2}), $ | (7) |
求出穿越单元表面的质量、动量及能量的流量
| $ \begin{gathered} \Delta M = {\rho _2}\Delta V,\hfill \\ \Delta Mom = {\rho _2}{u_2}\Delta V,\hfill \\ \Delta TE = {\rho _2}\left( {{e_t}} \right)\Delta V. \hfill \\ \end{gathered} $ | (8) |
式中:ρ2为相邻单元密度;et为单元质量的总能量;T为边界上单元面积上的面力;△V为时刻tn~tn + 1的一个时间步长内穿越该单元的表面体积流量。采用单点高斯积分,通过控制方程从而可以解出单元形心处的物理量(密度、流速、内能)在tn + 1时刻的值,得到从时刻tn至tn + 1的变化量关系。根据材料本构关系,可以进一步计算出压力值。
1.3 拉格朗日-欧拉流固耦合MSC.Dytran中的流固耦合计算就是拉格朗日域(固体)与欧拉域(流场)的耦合计算。本文采用的一般耦合法大多是拉格朗日的固体在欧拉的流场范围内运动,即拉格朗日域驱动欧拉域。流场虽有速度,但在流固耦合过程中欧拉网格不移动也不变形。
耦合的目的是为了让欧拉网格与拉格朗日网格发生相互作用。在默认设定下,欧拉求解器与拉格朗日求解器单独分开。当没有定义流体和固体之间耦合关系时,即使拉格朗日单元恰好处在欧拉网格范围内也不会对欧拉材料的流动产生任何影响,同时自身也不受任何来自欧拉材料力的作用。耦合关系的定义可以启动欧拉与拉格朗日单元之间的相互作用的计算程序,从而能够分析复杂的流固祸合问题。
2 仿真方法可靠性分析为了验证MSC.Dytran软件在计算流固耦合问题的可靠性,先对N.Aquelet[10]二维刚性楔形体(斜升角B=10°)等速入水模型进行仿真计算。本文建立了完整的二维模型,如图 1所示。

|
图 1 计算模型 Fig. 1 Calculation model |
楔形体结构用Lagrange四边形壳单元来离散,采用刚性材料,以5.425 m /s的速度等速入水,底部距液面的初始高度为0.02 m,流体材料用六面体的Euler单元来离散。为提高计算效率,在离楔形体较近的位置欧拉网格划分较密,离楔形体较远的位置网格划分较为稀疏。Euler,Lagrange单元的尺寸比约为1:1.2。如图 1所示,上层欧拉网格为空气域,用可压缩理想气体的材料来填充;下层欧拉网格为水域,用无粘性、可压缩的理想流体的材料填充。空气域压力用状态方程EOSGAM描述,水区域压力用多项式状态方程EOSPOL描述。楔形体的外表面为流固耦合面,采用一般耦合算法,考虑到问题的二维性,模型在z方向上取单位长度,且在欧拉单元的z+,z-前后表面上施加刚性墙边界以保证流场仅在xoy平面内运动,而楔形体也只允许有y方向上的运动。根据Chuang[11]的观点,为了保证压力波在流场中传播不至于反射回来影响砰击区域,本文所选取的水域的宽度满足如下条件:
| $ {W_T} = 12{L_m}. $ | (9) |
式中:WT为流场的宽度;Lm为楔形体的半宽。
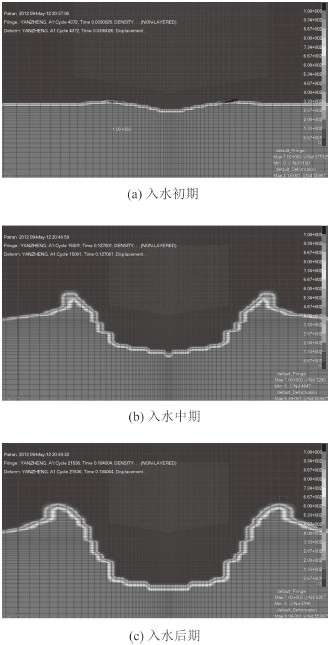
图 2为楔形体入水时水域压力云图;图 3为斜底最大砰击压力的时间历程,图中曲线(1)为本文仿真解,曲线(2)为文献[10]理论解,曲线(3)为文献[10]数值解;图 4为各个阶段自由液面的变化情况。

|
图 2 水域的压力云图 Fig. 2 Pressure cloud image |

|
图 3 斜底最大砰击压力时历曲线 Fig. 3 The curve of the maximum pressure |
|
图 4 楔形体入水自由液面变化情况 Fig. 4 The change of the water level of the wedge into the water |
读取图中时间历程数据可得,本文仿真解最大砰击压力为1.286 MPa,而文献中的理论解的最大砰击压力为1.2 MPa,数值解最大砰击压力为1.22 MPa,本文仿真解略大于文献中的解,相对于理论解的误差为7.16%,相对于数值解的误差为5.40%,均在7%左右,说明本文仿真计算具有可靠性。
3 船舶砰击计算模型在MSC.Dytran软件计算入水砰击问题可靠性的基础上,针对某大型集装箱船进行全船建模,计算船舶艏部舷侧区域的外飘砰击压力。该船主尺度:总长275.2 m,船宽32.3 m,型深21.8 m,设计吃水12.2 m。
3.1 计算工况针对船舶航行过程中较危险海况及常见航速,选取了6种工况进行计算,计算工况如表 1所示。
|
|
表 1 计算工况 Tab.1 Calculation condition |
运用基于非线性时域势流理论的Rankine面元法,对集装箱船型在上述工况下的运动响应进行预报。最终得到的船舶运动参数见表 2。
|
|
表 2 船舶运动参数 Tab.2 Ship motion parameters |
建立了整船模型,如图 5所示,并将船体模型进行网格划分,建立水域并进行计算参数的设置。

|
图 5 全船模型 Fig. 5 Whole ship model |
船体结构采用拉格朗日4节点四边形单元划分。船体网格划分模型如图 6所示。由于不考虑结构的局部变形和结构在砰击作用下在水中的振动,故将船体结构设置为刚体材料。水域单元为欧拉六面体实体单元。如图 6所示,上层欧拉网格为空气域,下层欧拉网格为水域。Euler与Lagrange单元的尺寸比为0.6:1。
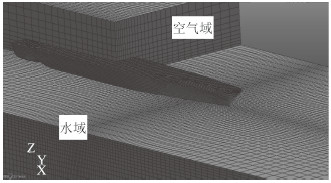
|
图 6 有限元模型 Fig. 6 Finite element model |
模型入水运动状态定义为强迫运动,模型运动由船舶沿航向的运动、垂荡运动以及纵摇运动耦合而成,更真实的模拟了船舶在实际航行过程中发生砰击时的运动状态,同时也考虑了全船仿真时入水砰击的三维特性。将表 2中的运动参数作为船舶运动的输入条件。
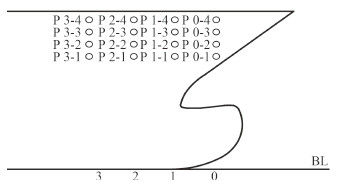
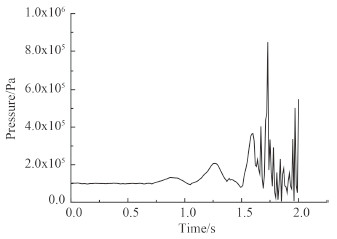
4 结果分析如图 7所示,取船舷侧0~3站,16~19号水线上的16个预报点读取砰击压力值。下面列出有义波高14 m,航速分别为0 kn,10 kn,18 kn三种工况下某预报点的砰击压力时历曲线,如图 8~图 10所示。
|
图 7 外飘砰击预报点位置示意图 Fig. 7 A sketch map of the prediction point of the flare slamming |
|
图 8 航速0 kn下2–1点时历曲线 Fig. 8 2–1 point time history curve at speed of 0kn |

|
图 9 航速10 kn时2–1点时历曲线 Fig. 9 2–1 point time history curve at speed of 10kn |
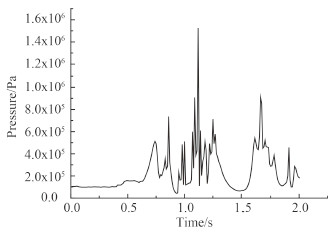
|
图 10 航速18 kn时2–1点时历曲线 Fig. 10 2–1 point time history curve at speed of 18kn |
在图 8~图 10中,对比有义波高为14 m时,航速18 kn,10 kn,0 kn两种工况的砰击压力值,可以看出,同样海况下,有航速时预报点的砰击压力值普遍大于无航速情况。
同样,由图 11可看出,航速18 kn,有义波高14 m工况下的砰击压力极值比航速10 kn, 有义波高18.5 m工况下砰击压力极值要高。一般情况下,海况越高,船舶受到的砰击压力越大,而此时当海况由浪高18.5 m降至14 m时,航速提高至18 kn反而使砰击压力更大,说明航速是影响船舶砰击压力大小的重要因素之一。
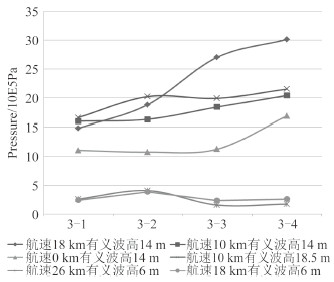
|
图 11 极值沿舷侧高度分布曲线 Fig. 11 Extreme value side along the height distribution curve |
当考虑船体的纵摇运动时,航速对于船首砰击压力的影响显著,可总结其规律为:航速越高,船首砰击压力越大。
4.2 航速对砰击压力极值分布的影响从图 12可以观察到,总共6个不同工况下的砰击压力极值曲线,6个不同工况包含了4个不同航速,可以发现,航速为0 kn与10 kn的曲线的峰值发生在3-1预报点处,航速为18 kn的曲线的峰值发生在2-1预报点处,航速为26 kn的曲线的峰值发生在1-1预报点处。可以发现,航速越高,砰击压力极值发生的点越往船尾推移。且航速为0 kn的曲线,砰击压力值增长的速度比航速为10 kn的曲线要慢,可以推断,航速0 kn下比航速10 kn下砰击压力峰值发生点更靠近船首。由此可以总结得出航速对于船首砰击压力极值分布的影响为:航速越高,船首砰击压力极值发生点越向船尾方向推移。由于图 12曲线中,航速相同,海况不同时峰值发生位置相同,故可进一步推断,砰击压力极值点发生位置在船长方向上并不受海况的影响,只与航速的高低有关。
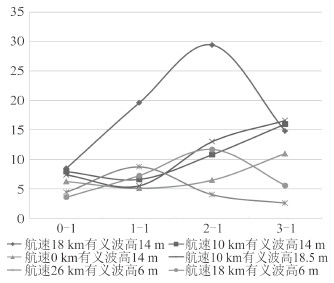
|
图 12 极值沿船长方向分布曲线 Fig. 12 Extreme value side along the direction of ship distribution curve |
分析其主要原因是,全船建模仿真时,将船舶的纵摇运动考虑进去之后,入水运动会改变船舶首部区域纵向剖面与水面的纵向斜升角θ,当船首入水时,θ会随着船舶纵摇角度的增大而减小,当纵摇角速度一定时,航速越大,船舶纵向剖面的入水速度也越大,由于纵向斜升角θ的减小,根据Wagner[12]的理论,入水冲击压力写为:
| $ {p_i} = \rho {K_w}V_n^2/text" $ | (10) |
式中:ρ为水密度;V为入水速度;K为无因次压力系数,取值根据有效冲击角
由文献[11]中总结的结论,物体入水角度变小,则砰击压力系数K增大。当K与V同时增大时,入水冲击压力pi会显著增大,则纵向剖面入水产生的压力会明显变大。
5 结语本文基于船舶全船建模,对某集装箱船外飘砰击过程进行了数值仿真,得到如下结论:
1)全船入水仿真时,纵摇运动导致船型纵向斜升角变小,从而导致航速对于船首外飘砰击压力大小的影响较大,其规律为航速越高,船首砰击压力越大。
2)全船入水仿真时,航速越高,船首砰击压力极值发生点越向船尾推移。
3)与船首局部建模或二维船体剖面建模相比,本文中尝试的将船舶的航速与纵摇运动考虑进去的全船建模仿真方法能更贴近实船运动模式,考虑的因素更多,更全面。
| [1] | 戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007 . |
| [2] |
向红贵.高速船甲板上浪的数值模拟研究[D].上海:上海交通大学, 2008.
XIANG Hong-gui. Numerical simulation of green water occurrence of high speed vessels[D]. Shanghai: Shanghai Jiaotong University, 2008. http://cdmd.cnki.com.cn/article/cdmd-10248-2009225656.htm |
| [3] |
文志飞.船舶砰击载荷的计算方法研究[D].哈尔滨:哈尔滨工程大学, 2010.
WEN Zhi-fei. A computational method for slamming loads of ship[D]. Harbin: Harbin Engineering University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10217-1011020960.htm |
| [4] |
孙峰, 吴卫国. 江海直达船船首入水砰击研究[J]. 交通科技 , 2011 (5) :114–116.
SUN Feng, WU Wei-guo. Impacting study on the water entry of the bow of river-sea ship[J]. Transportation Science & Technology , 2011 (5) :114–116. |
| [5] |
刘正国, 吴卫国, 潘晋, 等. 基于船波相对运动的船首砰击仿真方法[J]. 中国舰船研究 , 2013, 8 (6) :20–26.
LIU Zheng-guo, WU Wei-guo, PAN Jin, et al. Simulation method for the slamming problems of ship bows based on the relative motion between hulls and wave surfaces[J]. Chinese Journal of Ship Research , 2013, 8 (6) :20–26. |
| [6] |
胥飞, 刘桦. 艏外飘型船体入水砰击的二维SPH模拟[J]. 水动力学研究与进展 , 2013, 8 (5) :585–590.
XU Fei, LIU Hua. Numerical simulation of 2-D bow flare slamming using SPH method[J]. Chinese Journal of Hydrodynamics , 2013, 8 (5) :585–590. |
| [7] | AARSNES J V. Drop test with ship sections-effect of roll angle[R]. Marintek Report, Trondheim: Norwegian Marine Technology Research Institute, 1996. |
| [8] | ARAI M, TASAKI R. A numerical study of water entrance of two-dimensional wedges-effect of gravity, spray generation and vertical load[C]//Proceedings of the 3rd International Symposium on Practical Design of Ships and Mobile Units. Trondheim, Norway: Norwegian Institute of Technology, 1987. |
| [9] |
陈震, 冯永军, 肖熙. 大型集装箱船舷侧外飘砰击特性研究[J]. 船海工程 , 2011, 40 (3) :1–4, 9.
CHEN Zhen, FENG Yong-jun, XIAO Xi. Study on flare impact characteristics of large container ships[J]. Ship & Ocean Engineering , 2011, 40 (3) :1–4, 9. |
| [10] | AQUELET N, SOULI M, OLOVSSON L. Euler-Lagrange coupling with damping effects: application to slamming problems[J]. Computer Methods in Applied Mechanics and Engineering , 2006, 195 (1/3) :110–132. |
| [11] | STAVOVY A B, CHUANG S L. Analytical determination of slamming pressures for high-speed vehicles in waves[J]. Journal of Ship Research , 1967, 20 (4) :190–198. |
| [12] | Wagner H. Über Stoß-und Gleitvorgänge an der Oberfläche von Flüssigkeiten[J]. Zeitschrift für Angewandte Mathematik und Mechanik , 1932, 12 (4) :193–215. DOI:10.1002/(ISSN)1521-4001 |
 2016, Vol. 38
2016, Vol. 38
