小水线面双体船(Small Waterplane Area Twin Hull, SWATH)耐波性能优异,较传统单体船而言具有波浪中的运动响应幅值较小、共振频率较低及波浪中失速小等优点[1-3],但其较小的水线面一方面使得船体兴波较小;另一方面则导致该船型的纵向运动恢复力和力矩较小,纵向运动幅度较大,很容易出现纵向运动失稳,往往需要通过加装稳定鳍等附体来改善其纵向稳定性。同时,SWATH船片体间的相互干扰也会对其在波浪中的运动响应产生一定的影响。
对于SWATH船在波浪中的纵向运动特性以及片体间相互干扰对其在波浪中运动响应影响的研究,目前国内外选用的方法主要有:模型试验方法[4-5]、势流理论方法[6-7]和粘性CFD方法[8-9]。采用模型试验的方法最为有效,但模型试验周期长、成本高;势流理论方法应用广泛,但该方法对于稳定鳍以及粘性影响的处理大多选用Lee C. M.提出的修正办法[10-11],其精度受船型、稳定鳍剖面翼型以及粘性系数选取的影响;随着计算机性能和数值计算方法的飞速发展,采用粘性CFD方法对其运动特性开展分析成为可能,相比于模型试验方法,CFD方法具有成本低、无触点流场测量等优势;而相比于势流理论方法,CFD方法则可以充分考虑流体粘性及各种非线性因素(自由液面的破碎、甲板上浪、连接桥入水等)的影响。
本文选用基于RANS方程的粘性CFD方法,首先验证了该方法对于求解SWATH船在波浪中运动问题的有效性,进而采用该方法对一艘SWATH船在顶浪规则波中的纵向运动响应特性及其产生的机理进行探讨,初步分析并得到了船体运动响应曲线中各峰值产生的原因及片体间相互干扰对SWATH船在波浪中运动响应的影响规律。
1 数值波浪水池 1.1 控制方程及湍流模型RANS方程是粘性流体运动学和动力学的控制方程,文中以它作为求解船体粘性兴波流场的基本方程。其具体形式如下:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[{\mu (\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}) - } \right.\\ \left. {\frac{2}{3}\mu \frac{{\partial {u_l}}}{{\partial {x_l}}}{\delta _{ij}}} \right] + \frac{\partial }{{\partial {x_j}}}( - \rho \overline {{u_i}'{u_j}'} ) + \rho {f_i}, \end{array} $ | (1) |
式中:ρ为流体密度;μ为流体粘度;p为静压;fi为单位质量的质量力;ui和uj为速度分量。湍流模式为RNG k-ε模型。采用流体积法(Volume of Fluid Method, VOF)求解自由面兴波[12]。
1.2 造波与消波采用在入口边界模拟柔性造波板运动的速度分布产生入射波。根据无限水深中的线性波浪理论, 规则波的自由波面可以表达为:
| $ \zeta = a\cos (kx - \omega t), $ | (2) |
速度场为:
| $ \left\{ \begin{array}{l} u = a\omega {e^{kz}}\cos (kx - \omega t),\\ v = 0,\\ w = a\omega {e^{kz}}\sin (kx - \omega t) \end{array} \right. $ | (3) |
式中:ζ为自由面各点垂向位置;u、v和w分别为流体各点的纵向、水平方向和垂向的速度分量;a为波幅,k为波数;λ为波长;ω为波浪圆频率。
同时数值波浪水池在出口处设有消波区,通过在动量源函数中加入阻尼项,对流体质点垂向速度作强制衰减,具体过程见文献[13]。
2 计算方法验证 2.1 验证对象及流场设置本文验证对象为一艘小水线面双体船,安装有前后稳定鳍、舭龙骨,三维效果如图 1所示,模型水线长超过2.5 m,排水量超过200 kg。

|
图 1 模型三维示意图 Fig. 1 Three-dimensional model |
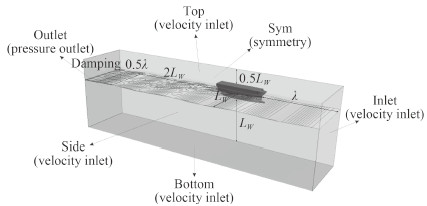
由于船体左右两舷对称,为减少计算量,计算对象为一半船体。采用六自由度求解器求解船体在波浪中的垂荡和纵摇运动[14],求解运动过程中,使用了地球坐标系和随船坐标系2个坐标系,地球坐标系原点位置与模型静止时右侧片体龙骨中点位置重合;随船坐标系与船体固联,其原点位于船体重心位置。计算流域在地球坐标系下为-(0.5 λ + 2.5 LW)<x<0.5 LW + λ,-LW<y<yG,-LW<z<D + 0.5 LW,其中λ为入射波长,yG为地球坐标系下船体重心横向位置坐标,计算流域及边界条件设置如图 2所示。
|
图 2 计算流域及边界条件设置 Fig. 2 Computational domain and boundary conditions |
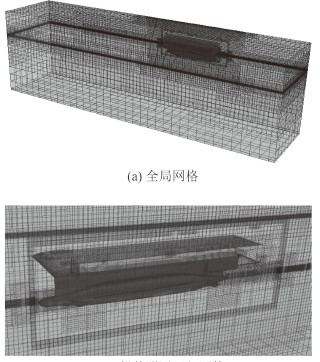
网格生成过程中对自由面及船体附近区域进行了加密,确保船体上游及附近每个波长不少于40个网格,每个波高不少于20个网格,船体的运动模拟应用了Overset重叠网格技术,网格划分情况如图 3所示,网格数量约270万,计算时间步长∆t=Te/200,Te为船体在波浪中运动的遭遇周期。
|
图 3 数值模拟网格 Fig. 3 Mesh used for numerical simulations |
为方便计算结果的比较和分析,定义无因次化运动响应传递函数如表 1所示。
|
|
表 1 运动响应传递函数定义 Tab.1 The definition of motion transfer functions |
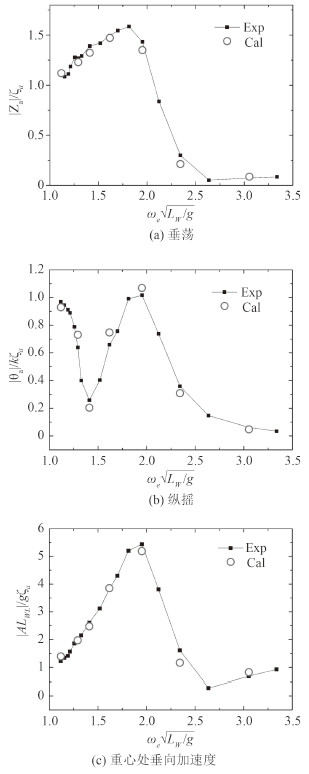
表 1中,ζa为入射波波幅,k为入射波波数,g为重力加速度。图 4给出了Fr=0.236,顶浪,波高H=1/50 LWL时的船体运动响应数值计算结果与试验结果的对比。
|
图 4 运动响应计算结果与试验结果对比 Fig. 4 Comparison of motion transfer functions between calculated results and experimental data |
由图 4可看出,计算所得运动响应整体趋势与试验结果一致,且吻合较好。这说明本文选取的计算方法及空间离散方法可靠,后续将基于此开展SWATH船在波浪中运动特性的分析。
3 顶浪规则波中SWATH船纵向运动数值分析 3.1 计算对象及工况本文研究对象为1艘安装有前后稳定鳍的小水线面双体船,三维效果如图 5所示,模型水线长超过3 m,排水量超过300 kg。船体计算流域、边界条件及网格划分均采取与3.1中相同的设置。本节针对该模型开展了Fr=0.11及Fr=0.21时船体在顶浪规则波中运动的数值模拟,波高H=0.1 m,λ/LW变化范围为0.4~7.1。

|
图 5 模型三维示意图 Fig. 5 Three-dimensional model |
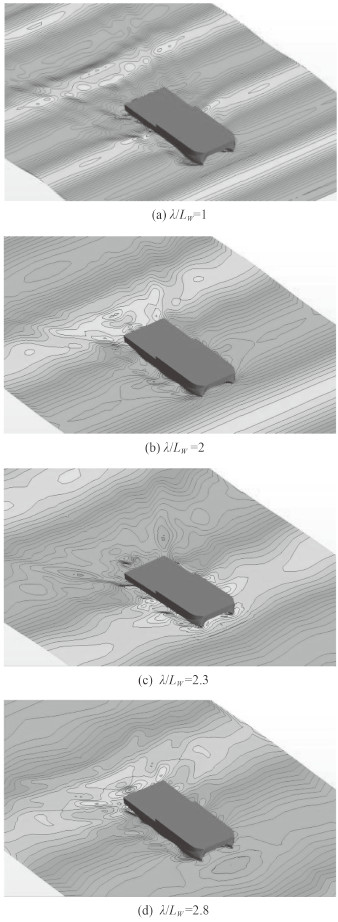
图 6给出了计算得到的Fr=0.21时不同入射波长条件下船体运动及自由面波形情况。图中可以明显观察到船体兴波与入射波的相互干扰。
|
图 6 船体在不同波长下自由面波形(Fr=0.21) Fig. 6 Ship motion and free surface at different wave length(Fr=0.21) |
图 7给出了Fr=0.11和Fr=0.21时,船体垂荡和纵摇运动传递函数随无因次化遭遇频率的变化曲线。可以看出,船体运动传递函数出现了2个峰值,为方便研究,将运动响应曲线中出现的峰值分别命名为P1,P2,如图 7所示。
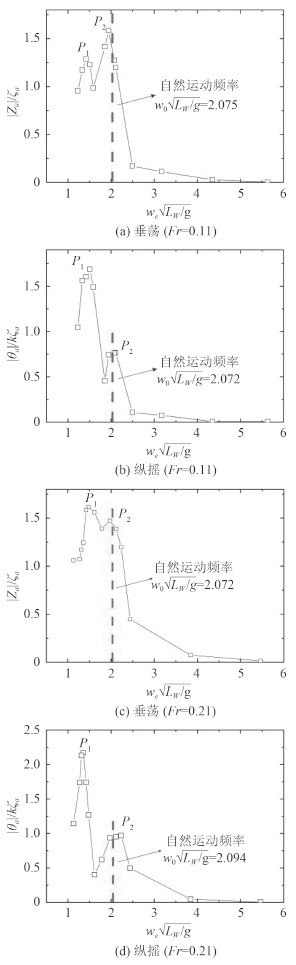
|
图 7 纵向运动传递函数(Fr=0.11,Fr=0.21) Fig. 7 Transfer functions of longitudinal motions(Fr=0.11, Fr=0.21) |
由图 7可看到,在不同航速下(Fr=0.11,Fr=0.21),船体运动传递函数的变化趋势基本一致。在低频段,船体运动传递函数相对较小;随着遭遇频率增加,垂荡和纵摇运动传递函数逐渐增大并出现峰值P1(垂荡出现在
为探究SWATH船运动响应峰值出现位置与其运动自然频率之间的关系,开展了对所研究SWATH船在静水中的纵向运动自由衰减数值模拟,得到了该SWATH船在不同航速下的纵向运动自然频率,如表 2所示。
|
|
表 2 船体纵向运动自然频率(Fr=0.11,Fr=0.21) Tab.2 The natural frequencies of ship longitudinal motions(Fr=0.11, Fr=0.21) |
由表 2可以看出,垂荡运动的自然频率相比纵摇略高,Fr=0.21时船体纵向运动自然频率较Fr=0.11高。将船体运动响应曲线与运动自然频率对比,如图 7所示,发现运动传递函数峰值P2出现位置与船体运动自然频率吻合,由此说明峰值P2产生原因为遭遇频率与运动自然频率相近,从而发生共振。
为进一步研究SWATH船在波浪中的纵向运动特性,本文将所研究小水线面双体船的一半作为单体船,由此得到一艘“小水线面单体船”(Small Waterplane Area Mono Hull,SWAMH),该SWAMH线型与SWATH一侧线型完全一致。对SWAMH开展了在波浪中运动的数值求解,计算工况为:Fr=0.11,顶浪,波高H=0.1 m,λ/LW变化范围为0.4~5.2。
图 8为SWATH和SWAMH在Fr=0.11,λ/LW=1时自由面情况对比,图中可以明显观察到SWATH两片体间兴波出现了相互干扰。

|
图 8 SWATH和SWAMH航行时自由面波形对比(λ/ LW=1) Fig. 8 Comparison of free surface between SWATH and SWAMH |
图 9给出了SWAMH运动的响应,并将其与SWATH的运动响应进行对比。由图可以看到,与SWATH运动响应类似,SWAMH的运动响应也出现了2个峰值,由此说明船体在低频段所出现的峰值P1可能与SWATH的船型及附体配置相关。
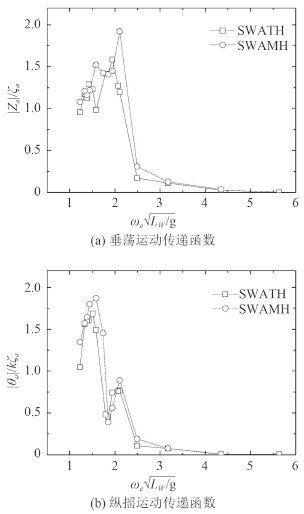
|
图 9 SWATH和SWAMH运动传递函数对比(Fr=0.11) Fig. 9 Comparison of motion transfer functions between SWATH and SWAMH(Fr=0.11) |
另外,相比于SWAMH船,SWATH船的运动响应整体偏小,尤其体现在峰值位置,且峰谷值出现的位置较单体船向低频方向偏移,该现象应该是由SWATH船两片体相互干扰引起。值得注意的是,该现象在垂荡运动响应中更为显著,由此说明相比于纵摇运动,片体间的相互干扰对SWATH船垂荡运动响应影响更大。
图 10为Fr=0.11时SWATH船所受垂向力和纵摇力矩与SWAMH的对比,图中垂向力Fz和纵摇力矩My分别比上ρgζaLWB'和ρgζaLW2B'进行无因次化,其中ρ为水密度,B'为SWAMH和SWATH对应的型宽。
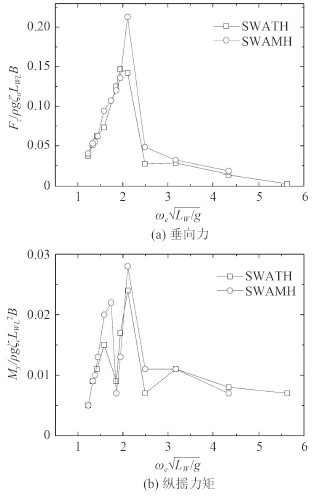
|
图 10 SWATH和SWAMH垂向力和纵摇力矩对比(Fr=0.11) Fig. 10 Comparison of vertical forces and pitchmoments between SWATH and SWAMH(Fr=0.11) |
由图 10可以看出,SWATH船所受的垂向力和纵摇力矩在峰值处均小于SWAMH,且峰值出现位置较SWAMH向低频方向偏移,该现象与SWATH和SWAMH运动响应对比结果一致。
4 结语本文采用RANS方法对SWATH船在顶浪规则波中的纵向运动特性开展了数值研究,较系统分析了船体纵向运动响应曲线中各峰值产生的原因及片体间相互干扰对SWATH船在顶浪规则波中运动响应的影响,得到以下结论:
1)船体在低频段出现的运动响应峰值P1可能与该SWATH船的船型及附体配置有关;运动响应峰值P2的出现则是因为此时船体遭遇频率接近其运动自然频率,由此发生运动共振。
2)片体间的水动力干扰效应使得SWATH船在波浪中运动响应峰值较单个片体响应峰值明显减小,且出现的位置向低频方向移动。相比于纵摇运动,片体间相互干扰对垂荡运动影响更大。
| [1] | 黄鼎良. 小水线面双体船性能原理[M]. 北京: 国防工业出版社, 1993 . |
| [2] |
董祖舜, 董文才. 小水线面双体船(SWATH)耐波性特点及影响因素分析[J]. 海军工程学院学报 , 1995 (1) :7–15.
DONG Zu-shun, DONG Wen-cai. Analysis of some influence factors on seakeeping of small waterplane area twin hull ships (SWATH)[J]. Journal of Naval University of Engineering , 1995 (1) :7–15. |
| [3] | SCHELLINE T E, PAPANIKOLOU A. Prediction of seakeeping performance of SWATH ships and comparison with measurements[C]//FAST' 91, 1st International Conference on Fast sea Transportation. Trondheim, Norway: Tapir Publishers, 811-826. |
| [4] | 夏向东.高速小水线面双体船水动力性能研究[D].武汉:海军工程大学, 2011. |
| [5] | BOUSCASSE B, BROGLIA R, STERN F. Experimental investigation of a fast catamaran in head waves[J]. Ocean Engineering , 2013, 72 :318–330. |
| [6] |
毛筱菲. 小水线面双体船在波浪中的运动响应预报[J]. 船海工程 , 2005 (4) :13–15.
MAO Xiao-fei. Numerical study of the motion response prediction of SWATH ship in waves[J]. Ship & Ocean Engineering , 2005 (4) :13–15. |
| [7] |
吴介, 谷家扬, 管义锋, 等. 基于Rankine源法的小水线面双体科考船耐波性预报[J]. 江苏科技大学学报(自然科学版) , 2015, 29 (2) :103–107.
WU Jie, GU Jia-yang, GUAN Yi-feng, et al. Prediction of SWATH research ship seakeeping performance based on the Rankine source method[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition) , 2015, 29 (2) :103–107. |
| [8] | QIAN P, YI H, LI Y H. Numerical and experimental studies on hydrodynamic performance of a small-waterplane-area-twin-hull (SWATH) Vehicle with inclined struts[J]. Ocean Engineering , 2015, 96 :181–191. |
| [9] | SHEN Z R, YE H X, WAN D C. URANS simulations of ship motion responses in long-crest irregular waves[J]. Journal of Hydrodynamics , 2014, 26 (3) :436–446. |
| [10] | LEE C M, CURPHEY R M. Prediction of motion, stability, and wave load of small-waterplane-area, twin-hull ships[C]//SNAME Transactions, 1977, 85: 94-130. |
| [11] | LEE C M. Theoretical prediction of motion of small-wat-erplane-area, twin-hulls (SWATH) ship in waves[R]. David Taylor NSRDC Report, 76-0046, Bathesda (Maryland): DTNSRDC, 1976. |
| [12] | RUSCHE H. Computational fluid dynamics of dispersed two-phase flows at high phase fractions[D]. UK: Imperial College, 2002. http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.402087 |
| [13] | CHOI J, YOON S B. Numerical simulations using momentum source wave-maker applied to RANS equation model[J]. Coastal Engineering , 2009, 56 (10) :1043–1060. |
| [14] | CARRICA P M, WILSON R V, NOACK R W, et al. Ship motions using single-phase level set with dynamic overset grids[J]. Computers & Fluids , 2007, 36 (9) :1415–1433. |
 2016, Vol. 38
2016, Vol. 38
